OpenGL入门1.0-初探

一、认知

在开始这段旅程之前我们先了解一下OpenGL到底是什么。OpenGL本身并不是一个API，它仅仅是一个由Khronos组织制定并维护的规范，规定了每个函数该如何执行以及它们的输出值，至于内部具体每个函数是如何实现，将由OpenGL库的开发者自行实现（一般是显卡生产商）。由于OpenGL是跨平台的，所以创建一个OpenGL上下文(Context)和一个用于显示的窗口在每个系统上都是不一样的，这意味着我们不得不自己处理创建窗口，定义OpenGL上下文以及处理用户输入。幸运的是每个平台的创建都会提供相应的实现，比如：Android平台中使用EGL、PC中比较流行的实现有GLFW等。

发展史：OpenGL主要有两个大版本改动，早期的OpenGL使用立即渲染模式（也称固定渲染管线），这种模式开发者很少能控制OpenGL如何进行计算的不够灵活。从OpenGL3.2开始使用核心模式，开发者可以把握OpenGL具体是如何运作的，提供了更多的灵活性，可以更深入的理解图形编程。

下面开始介绍两个概念：状态机、对象。这思想将贯彻OpenGL整个开发，重要，重要，重要。

1.状态机

只要你记住OpenGL本质上是个大状态机，就能更容易理解它的大部分特性，OpenGL的状态通常被称为OpenGL上下文(Context)。当使用OpenGL的时候，我们会遇到一些状态设置函数，这类函数将会改变上下文。以及状态使用函数，这类函数会根据当前OpenGL的状态执行一些操作。

glClearColor(0.2f, 0.3f, 0.3f, 1.0f);//状态设置
glClear(GL_COLOR_BUFFER_BIT);//状态使用

2.对象

在OpenGL中一个对象是指一些选项的集合，它代表OpenGL状态的一个子集。

// 创建对象
unsigned int objectId = 0;
glGenObject(1, &objectId);
// 绑定对象至上下文
glBindObject(GL_WINDOW_TARGET, objectId);
// 设置当前绑定到 GL_WINDOW_TARGET 的对象的一些选项
glSetObjectOption(GL_WINDOW_TARGET, GL_OPTION_WINDOW_WIDTH, 800);
glSetObjectOption(GL_WINDOW_TARGET, GL_OPTION_WINDOW_HEIGHT, 600);
// 将上下文对象设回默认
glBindObject(GL_WINDOW_TARGET, 0);

这一小段代码展现了你以后使用OpenGL时常见的工作流。我们首先创建一个对象，然后用一个id保存它的引用。然后我们将对象绑定至上下文的目标位置（GL_WINDOW_TARGET）。接下来我们设置窗口的选项。最后我们将目标位置的对象id设回0，解绑这个对象。设置的选项将被保存在objectId所引用的对象中，一旦我们重新绑定这个对象到GL_WINDOW_TARGET位置，这些选项就会重新生效。这样的好处就是，我们可以创建一个对象池（对象容器），使用OpenGL状态操作的时候，只需要绑定含有需要的设置对象，就能够渲染对应的画面，而不需要重复设置选项了。

二、GLSL语法

GLSL是为图形计算量身定制的类C语言写成的着色器语言（着色器是运行在GPU上的小程序，具体如何编写运用到OpenGL中下一章说明），下面来聊一聊它的语法结构和数据类型:

#version 330 core//版本名

in type in_variable_name;//输入变量
out type out_variable_name;//输出变量
//是一种从CPU中的应用向GPU中的着色器发送数据的方式，uniform声明的是全局变量，每个着色器中都可以访问，所以注意命名
uniform type uniform_name;

int main()//每个着色器的入口都是main函数
{
  // 处理输入并进行一些图形操作
  ...
  // 输出处理过的结果到输出变量
  out_variable_name = weird_stuff_we_processed;
}
//说明：广泛的说每个着色器的输入变量是上一个着色器的输出变量（当变量命名、类型相同时就可以传递下去）

1.数据类型

基础数据类型：int、float、double、uint和bool

两种容器： 向量（vector） 、矩阵（matrix）

1.1向量

向量是有一个方向和大小，它可以任意维度，在OpenGL中通常只使用2至4维。

数学含义：

点乘：两个向量的点乘等于它们的数乘结果乘以两个向量之间夹角的余弦值，使用点乘可以很容易测试两个向量是否正交或平行（正交意味着两个向量互为直角）
$$\bar{v}\cdot \bar{k}=||\bar{v}||\cdot ||\bar{k}||\cdot \cos \theta$$
叉乘：叉乘只在3D空间中有定义，它需要两个不平行向量作为输入，生成一个正交于两个输入向量的第三个向量。如果输入的两个向量也是正交的，那么叉乘之后将会产生3个互相正交的向量。

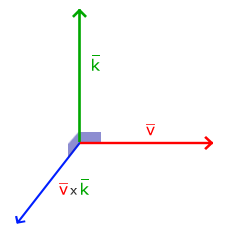
A和B叉积：
$$\left(\begin{array}{c}{A}_x\\ A_y\\ A_z\end{array}\right)\times \left(\begin{array}{c}{B}_x\\ B_y\\ B_z\end{array}\right)=\left(\begin{array}{c}{A}_y\cdot B_z-A_z\cdot B_y\\ A_z\cdot B_x-A_x\cdot B_z\\ A_x\cdot B_y-A_y\cdot B_x\end{array}\right)$$

1.2矩阵(矩阵执行顺序从右到左阅读)

可用于OpenGL各种图形变换操作,如下列举几种常用的操作

缩放：
$$\left[\begin{array}{cccc}{S}_1& 0& 0& 0\\ 0& S_2& 0& 0\\ 0& 0& S_3& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}{S}_1\cdot x\\ S_2\cdot y\\ S_3\cdot z\\ 1\end{array}\right)$$
位移：
$$\left[\begin{array}{cccc}1& 0& 0& T_x\\ 0& 1& 0& T_y\\ 0& 0& 1& T_z\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}x+T_x\\ y+T_y\\ z+T_z\\ 1\end{array}\right)$$
旋转

沿x轴旋转：
$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}x\\ \cos \theta \cdot y-\sin \theta \cdot z\\ \sin \theta \cdot y+\cos \theta \cdot z\\ 1\end{array}\right)$$
沿y轴旋转：
$$\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}\cos \theta \cdot x+\sin \theta \cdot z\\ y\\ -\sin \theta \cdot x+\cos \theta \cdot z\\ 1\end{array}\right)$$
沿z轴旋转：
$$\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left(\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right)=\left(\begin{array}{c}\cos \theta \cdot x-\sin \theta \cdot y\\ \sin \theta \cdot x+\cos \theta \cdot y\\ z\\ 1\end{array}\right)$$
任意旋转轴:
$$\left[\begin{array}{cccc}\cos \theta +{R_x}^2(1-\cos \theta )& R_x{R}_y(1-\cos \theta )-R_z\sin \theta & R_x{R}_z(1-\cos \theta )+R_y\sin \theta & 0\\ R_y{R}_x(1-\cos \theta )+R_z\sin \theta & \cos \theta +{R_y}^2(1-\cos \theta )& R_y{R}_z(1-\cos \theta )-R_x\sin \theta & 0\\ R_z{R}_x(1-\cos \theta )-R_y\sin \theta & R_z{R}_y(1-\cos \theta )+R_x\sin \theta & \cos \theta +{R_z}^2(1-\cos \theta )& 0\\ 0& 0& 0& 1\end{array}\right]$$
参考文献
LearnOpenGL中文官网