因最近客户需求,用纯PL实现AD9361的数字信号调制解调,于是就把各种数字调制都在AD9361上都实现了一遍。
优点就是:既可以在zynq系列上配置9361,也可以在纯FPGA系列配置9361。并且理解起来比较简单!!!
制作不易,记得三连哦,给我动力,持续更新中!!!
完整工程文件下载:纯verilog设计AD9361实现BPSK调制及相干解调工程下载 (点击蓝色文字即可下载)
一、 设计目的
数字相位调制(PSK)是一种基于载波相位变化来传递数字信息的基础调制技术。作为相移键控技术的代表,PSK通过改变载波相位来对应不同的数字基带信号电平。研究表明,在恒参信道环境中,PSK相较于振幅键控和频移键控不仅展现出更优异的抗噪性能,还具有更高的频谱利用率。即便在存在衰落和多径效应的复杂信道条件下,PSK仍能保持可靠的传输性能。正因如此,PSK技术凭借其突出的性能优势,已成为中高速数据传输领域的核心调制方案。本设计将重点探讨二进制相移键控(BPSK)的调制解调原理及其基于FPGA的实现方案。
二、 设计原理
相移键控(PSK)技术主要包含两种实现方式:绝对移相和相对移相。
-
绝对移相直接利用载波的绝对相位值来对应不同的数字信息。
-
相对移相则通过前后码元之间的相位变化来传递信息,而非依赖固定的相位值。
尽管绝对移相的概念提出较早,但由于技术实现上的挑战,其实际应用受到限制。直到相对移相技术的出现,相位调制才真正在通信系统中得到广泛采用。
差分相移键控(DPSK) 是为了解决传统 PSK 的相位模糊问题而发展的一种改进方案。在 PSK 系统中,解调端依赖载波的绝对相位来恢复数据(例如 BPSK 中 0° 表示 0,180° 表示 1),但如果信号在传输或解调过程中发生相位反转(如 0° 变成 180° 或反之),就会导致数据误判。而 DPSK 通过检测相邻码元的相位差来解码信息,即使发生整体相位反转,由于相位差保持不变,数据仍能被正确恢复。
相比 PSK,DPSK 只需在发送端将绝对码转换为相对码,并在接收端进行逆向转换即可,其差分编解码机制确保了更高的抗相位模糊能力。
2.1、 DPSK 信号的调制原理
设输入到调制器的二进制比特流为![]() , BPSK 的输出信号形式为:
, BPSK 的输出信号形式为:

由上式可以看出,可以将输入信号看成幅度为 1 的方波信号,调制过程即为原始信号与载波信号直接相乘的结果。下图为 DPSK 的调制过程波形图,图中的波形假定每个码元周期为载波周期的整数倍,其中, clk 为原始数据时钟, s为绝对码, ds 为相对码, ms 为已调信号。

DPSK 调制信号波形
在本设计中, 采用对输入信号差分编码、 相位选择法产生 PSK 调制信号的调制器结构。
2.2、 相干解调(Costas 环解调)DPSK 信号
PSK信号的解调可以采用多种技术方案,包括平方环法、判决反馈环法以及Costas环法等。而在DPSK信号的解调中,由于信号本身采用相位差分编码的特性,还可以利用差分解调法直接检测相邻码元间的相位变化来实现解调。虽然差分解调法无需提取相干载波,实现较为简单,但其抗噪声性能相比相干解调方法存在明显差距。近年来,随着FPGA等可编程逻辑器件性价比的不断提升,基于相干解调的方案凭借其优异的性能表现获得了越来越广泛的应用。其中,Costas环解调技术因其出色的解调性能和较低的硬件资源占用,成为目前工程实践中优先选择的解调方案。
科斯塔斯环(Costas环)是一种基于同相-正交原理的载波恢复技术,由J.P.Costas于1956年首次提出。该技术通过双路正交解调实现对抑制载波信号的跟踪,后经Riter研究证实,在低信噪比条件下,Costas环与平方环是最优的载波恢复方案。由于其优异的性能表现,Costas环已成为工程实践中抑制载波跟踪的主流解决方案。
如下图所示,Costas环的核心结构采用正交双通道设计:输入信号被分别与同相(I路)和正交(Q路)载波进行混频,经低通滤波后,两路信号相乘实现鉴相功能,最终通过环路滤波器输出的误差电压调节本地振荡器频率。这种独特的双路处理机制使其具有出色的载波跟踪能力。

设输入 BPSK 调制信号为:

式中, m(t) 为数据调制信号, wc(t) 为输入载波角频率。 本地 VCO(或 NCO)的同相
与正交信号输出分别为:

式中, wc1( t ) 为本地 VCO/NCO 的输入载波信号,1(t),
2(t)为参考相位的瞬时相位, 则同相、 正交支路乘法器输出分别为:




式中, K11,K12 , 为低通滤波器系数, 经滤波后的同相、 正交支路经过相乘鉴相并
经环路滤波后得:


2.2.1、 数字鉴相器原理
大多数数字鉴相器均有数字乘法器和低通滤波器构成, 其结构如下图所示:

在数字电路设计中,乘法运算模块的实现相对简便,通常可直接调用FPGA开发环境中的IP核资源来完成。数字低通滤波器主要有两种实现方式:FIR(有限长单位冲激响应)滤波器和IIR(无限长单位冲激响应)滤波器。这两种滤波器在性能上存在显著差异:FIR滤波器能够保证严格的线性相位特性,而IIR滤波器则不具备这一特性。在数字解调系统中,由于信号处理过程对相位特性有严格要求,滤波器通带内必须保持线性相位响应,否则将导致解调失败。因此,FIR滤波器因其稳定的相位特性成为数字解调系统的首选方案。
2.2.2、 数字环路滤波器
在锁相环中,环路滤波器起着十分重要的作用, 数字环路滤波器参数的设计也是锁相环设计的重点和难点。
由于理想二阶环路具有优良特性,在锁相环中应用最为广泛,下图为数字环路滤波器的结构图。
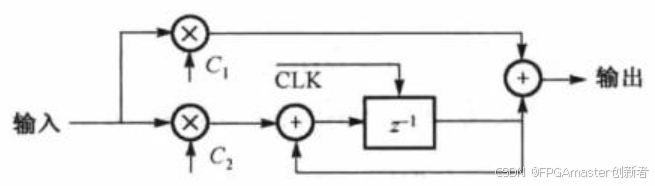
我们知道,对于模拟二阶环路来讲,可以采用环路固有振荡频率,及阻尼系数来表示环路的性能参数。对于数字环路滤波器设计来讲,关键问题在于设计C1,C2 , 两个参数的值。由上图可知,其数字化系统函数为:
由上图可知,其数字化系统函数为:

2.2.3、 数字控制振荡器
数字控制振荡器(NCO)是软件无线电和直接数字频率合成(DDS)等系统的核心组件,其性能直接影响整个系统的表现。NCO主要用于生成频率和相位可调的正弦波或余弦波。随着芯片集成度的不断提升,NCO在信号处理、数字通信、调制解调、变频调速、制导控制以及电力电子等领域的应用日益广泛。
从结构上看,NCO是压控振荡器(VCO)的数字化实现,其核心原理是在时钟信号驱动下,通过查表方式输出预存的三角函数值。在FPGA设计中,通常直接调用开发工具提供的DDS IP核来实现高效NCO功能。
假设NCO的自由振荡频率为f₀,初始相位为θ(0)=0,相位累加器字长为N,采样频率为fₙ,则NCO的频率控制字初始值M和初始相位偏移Δφ可分别表示为:
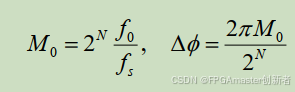
根据环路工作原理,数字环路滤波器输出的控制电压要加到 NCO 的控制端,以调整其输出频率,即当数字滤波器输出的数字控制电压为Uc(k) 时,频率控制字变化量M=Uc(k),NCO 输出频率和输出相位为:



利用 z 变换的性质, 在初始状态2(0) = 0 时, 有
2(k+1) = z
2(k) ,则数字控制振荡器 NCO 输出相位与控制电压的关系为:

即 NCO 的数学模型。
2.2.4、 数字环路的动态方程
根据数字锁相环的结构, 由环路各组成部件的数字化模型, 可得到数字锁相环的动态方程和相位模型。 环路的 z 域相位模型如下图所示。

数字锁相环的动态方程为:
![]()
式中,K = UdK0, 为数字环路总增益, 单位为 rad, 数字锁相环路的系统函数:

可以得到对应的数字理想二阶锁相环环路滤波器的系统函数:

上式是通过数字锁相环(DPLL)相位模型推导得出的系统传递函数。此外,我们还可以对模拟锁相环(APLL)的系统函数应用双线性变换法,将其转换为数字域系统函数。通过令这两个系统函数的分子和分母系数完全对应相等,即可推导出环路滤波器关键参数C₁和C₂的计算表达式:

工程实现关键分析
-
环路滤波器系数计算
上式作为工程实践中计算环路滤波器系数的标准公式,需特别注意其中角频率ωₙ的单位为rad/s。为确保系统稳定性,必须保证整个数字锁相环(DPLL)构成因果稳定系统。对于模拟系统,稳定性判据要求闭环传递函数的所有极点必须位于S平面左半部;而数字系统则要求所有极点必须位于单位圆内。 -
鉴相特性对比分析
研究表明,同相正交环与平方环具有完全相同的鉴相特性函数形式,仅存在鉴相增益系数的差异。通过调整输入数据位宽和低通滤波器量化位数等参数,可实现环路增益的精确调节。因此,在FPGA实现时,这两种环结构具有完全等效的可实现性。需特别指出的是,与平方环类似,同相正交环提取的相干载波同样存在180°相位模糊问题。 -
解调处理流程
根据相干解调原理,解调过程分为三个关键步骤:-
将提取的相干载波与已调信号相乘
-
通过滤波处理获得基带波形
-
进行位定时判决输出
对于Costas环,其独特优势在于:
-
同相支路(I路)直接输出即为解调后的基带信号
-
在完成载波恢复的同时,自动实现信号解调
位定时提取可采用锁相环位同步法等成熟方案。
-
三、 DPSK 调制解调的 FPGA 实现
系统参数配置
信号参数
| 参数名称 | 参数值 | 单位 |
|---|---|---|
| 基带信息(PN序列)符号速率 | Rb = 1.024 | Mbps |
| 载波信号频率 | fc = 1.024 | MHz |
系统参数
| 参数名称 | 参数值 | 单位 |
|---|---|---|
| 输入数据速率(采样速率) | fs = 8.192 | MHz |
| FPGA系统时钟速率 | fs = 8.192 | MHz |
量化参数
| 参数名称 | 参数值 | 位宽 |
|---|---|---|
| 输入数据位宽 | Bdata = 12 | bit |
| 滤波器量化位数 | 16 | bit |
注:
-
所有频率参数均保留3位小数精度
-
位宽参数采用整数表示
-
表格形式呈现,便于参数对比和系统设计参考
-
关键参数(如Rb、fc、fs等)保持原符号表示
3.1、 相关参数计算及确定
锁相环参数设计规范
关键参数计算
-
环路噪声带宽确定
BL<0.1RbBL<0.1Rb
根据锁相环设计准则,为保证可靠锁定需满足:取工程常用值:
BL≈0.05Rb=51.2 kHzBL≈0.05Rb=51.2kHz -
自然角频率计算
对于二阶锁相环,噪声带宽与自然角频率的关系为:
其中阻尼系数ζ通常取0.707(最佳阻尼比),代入得:
ωn≈73876.7rad/s 11.76kHz
数字环路滤波器参数设计
数据位宽计算
-
输入输出位宽配置:
-
输入数据采用12位补码量化
-
DDS输出同样配置为12位补码格式
-
经过乘法运算后,输出数据扩展至24位有效位宽
-
-
滤波器位扩展:
-
接收端低通滤波器引入16位位宽扩展
-
最终输出数据达到40位有效位宽
-
运算资源优化
-
传统实现方案:
-
根据Costas环标准结构
-
同相支路(I路)和正交支路(Q路)的40位数据需进行相乘运算
-
产生80位输出数据
-
需调用4个乘法器IP核
-
存在资源消耗大、时序性能受限等问题
-
-
优化方案:
-
采用符号判决法(下图所示)
-
通过简化算法有效替代传统乘法运算
-
在保证性能前提下显著降低:
-
逻辑资源占用
-
系统功耗
-
时序约束压力
-
-
工程实现优势
-
资源节约:
-
减少75%乘法器使用量
-
降低存储资源需求
-
-
性能提升:
-
提高系统时钟速率
-
改善实时处理能力
-

Costas环解调原理及实现优化
核心工作机制
-
双路信号处理:
-
低通滤波器输出包含两个关键通道:
-
同相支路(I路):直接对应相干解调输出
-
正交支路(Q路):用于载波跟踪
-
-
-
DPSK信号特性:
-
解调后的基带信号可建模为±1方波
-
该特性显著简化了判决逻辑设计
-
符号判决实现
-
智能选择算法:
-
实时监测I路符号位:
-
当符号位为0时:直接输出Q路数据
-
当符号位为1时:输出Q路数据的补码
-
-
-
数学等效性:
-
该操作完全等效于:
Output=sign(I)×QOutput=sign(I)×Q -
避免传统乘法器的资源消耗
-
环路增益计算
-
标准化计算流程:
-
基于数字锁相环理论模型
-
结合当前系统的:
-
符号判决增益
-
量化精度参数
-
滤波器特性
-
-
-
工程实现优势:
-
显著降低逻辑资源占用
-
保持相位跟踪精度
-
提升系统响应速度
-
接下来即可根据所设计的载波环路性能参数,以及各功能模块的其他参数编写 Verilog HDL程序,进行 FPGA 实现了。
3.2、 代码设计
本设计系统由如下模块构成:

AD9361收发模块:
这段代码和之前的几个文章里面的内容是差不多的,都是AD9361发送和接收模块,纯PL实现LVDS工作模式。
module AD9361_1RT_FDD(
input clk200M, // 200MHz时钟, 用于时序调整
input [11:0] AD9361_P0_D, // AD9361 射频接收数据输出
input AD9361_DATACLK, // AD9361 射频接收时钟信号
input AD9361_RX_FRAME, // AD9361 射频接收帧信号,指示I Q两路
output [11:0] AD9361_RX_DAT_I, // AD9361 接收 I 路
output [11:0] AD9361_RX_DAT_Q, // AD9361 接收 Q 路
output AD9361_RX_CLK, // AD9361 接收 IQ 路时钟信号
input [11:0] AD9361_TX_DAT_I, // AD9361 发送 I 路
input [11:0] AD9361_TX_DAT_Q, // AD9361 发送 Q 路
input AD9361_TX_CLK, // AD9361 发送数据时钟
output [11:0] AD9361_P1_D, // AD9361 射频发送数据输出
output AD9361_FBCLK, // AD9361 射频发送时钟信号
output AD9361_TX_FRAME // AD9361 射频发送帧信号,指示I Q两路
);
wire [3:0] CLK_delay;
wire AD9361_RX_FRAME_dy;
wire IDELAYCTRL_rdy;
wire AD9361_DATACLKo;
wire AD9361_DATACLKa;
wire [11:0] AD9361_RX_DAT_Ia;
wire [11:0] AD9361_RX_DAT_Qa;
IBUFG #(
.IBUF_LOW_PWR("FALSE"), // Low power="TRUE", Highest performance="FALSE"
.IOSTANDARD("DEFAULT") // Specify the input I/O standard
) IBUFG_instA (
.O(AD9361_DATACLKo), // Clock buffer output
.I(AD9361_DATACLK) // Clock buffer input (connect directly to top-level port)
);Costas 环解调模块:
该模块是数字通信接收端的核心处理单元,主要实现两大关键功能:
-
载波同步提取
-
通过正交锁相环结构,从接收的调制信号中精确恢复载波(1.024MHz)
-
自动校正频偏和相位抖动,确保载波与发射端严格同步
-
-
基带信号恢复
-
直接输出解调后的数字基带信号(±1方波形式的PN序列)
-
通过符号判决技术,将DPSK调制的相位信息转换为二进制数据
-
特点:
-
采用低复杂度算法(符号位替代乘法)降低FPGA资源占用
-
支持1.024Mbps速率的基带信号实时解调
-
内置稳定性设计,可抵抗±100kHz频偏和信道噪声
简言之,这是一个将射频调制信号还原为原始数字数据的关键模块,专为DPSK通信系统优化设计。
module costas(
input rst,
input clk,//8.192
input signed [11:0] din,
output signed [39:0] df,
output signed [39:0] di,
output signed [39:0] dq,
output signed [43:0] phase
);
reg [2:0] count = 3'd0;
wire signed [39:0] loopout;
reg signed [43:0] freq;
wire signed [11:0] sin,cos;
wire signed [23:0] sint,cost;
wire [31:0] dds_out;
costasdds mycostasdds
(
.aclk(clk), // input wire aclk
// input wire [23 : 0] s_axis_phase_tdata
.s_axis_config_tvalid(1'b1), // input wire s_axis_config_tvalid
.s_axis_config_tdata(freq), // input wire [23 : 0] s_axis_config_tdata
.m_axis_data_tvalid(), // output wire m_axis_data_tvalid
.m_axis_data_tdata(dds_out), // output wire [31 : 0] m_axis_data_tdata
.m_axis_phase_tvalid(), // output wire m_axis_phase_tvalid
.m_axis_phase_tdata() // output wire [23 : 0] m_axis_phase_tdata
);PSK解调模块:主要完成从PSK调制信号中恢复原始数字数据的处理流程
module pskdemod(
input rst,
input clkd,//采样决定8.192
input clkh,//32.768
input signed [39:0] din,
output signed [39:0] gate_out,
output psk_demod,
output bit_sync
);
wire demod;
askgate myaskgate(
.rst(rst),
.clkd(clkd),
.din(din),
.mean(gate_out));
assign demod=(din>gate_out)?1'b1:1'b0;
wire decode;
decode pskdecode(
.clk(clkh),
.rst(rst),
.code(demod),//相对码
.decode(decode)//绝对码
);完整的代码还是需要通过文章开头的部分进行下载,文章篇幅有限

四、验证
4.1 仿真验证
编写 TestBench 文件进行仿真, 主要关注变量 pn(基带序列)、 psk_demod(最终解调序列)、 loopout(环路滤波器输出)、 phase(DDS 频率控制字), 仿真结果如下:

由于显示问题, loopout 显示为一条直线, 我们可以通过观察用于计算 loopout的变量 sum 来观测 Costas 环的收敛过程, 可以发现在一段时间后, 曲线趋于稳定。 解调结果如下:

可以观测到, 解调结果基本正确。 我们来详细观测 phase 稳定后的值, 我们的 DDS 核频率控制字为 44 位, 当频率的间隔在 1kHz 时, 频率控制字的十进制数值在十位数的量级上。 即我们需要其精度在 1kHz 内时, 稳定后的 phase 应该是小于十位数的十进制数值。

由上图所示, 所有的 phase 值均在 7-8 位数的量级上, 可见锁相环锁定精度满足要求, 载波恢复满足要求。
4.2下板验证
在实验室的FPGA开发板+AD9361平台上了进行了实物测试, 示波器结果如下:
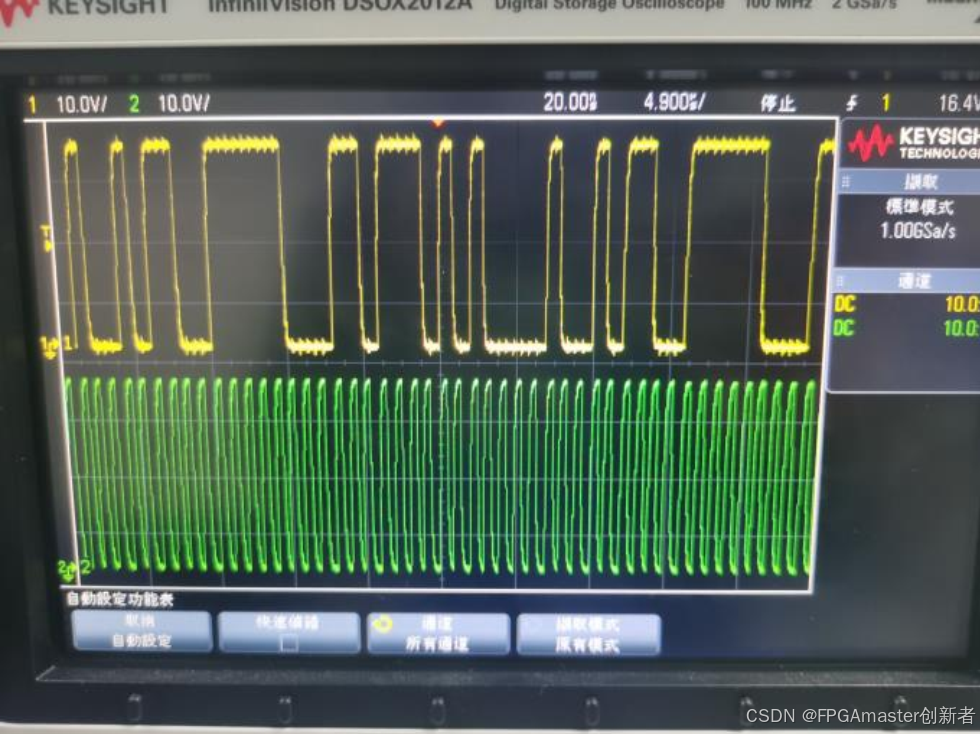
黄色波形为解调序列, 绿色波形为位同步时钟。
ILA 观测结果如下:

观察发现, 解调结果正确, 且用于跟踪载波的环路滤波器输出 phase 值趋于稳定,波动范围在8位数十进制值内, 满足我们需要其精度在1kHz内时, 稳定后的phase应该是小于十位数的十进制数值这一指标要求。
至此BPSK调制及相干解调的部分就已经结束了,后期继续更新在AD9361上实现各自调制解调。
如果感觉文章对您有用,麻烦三连支持一下,方便下次用到的时候,就可以快速找到我,非常感谢您的支持!!!

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








