用Excel绘制统计图

个人学习笔记，课程为数学建模清风付费课程

一、简述

       这一节虽然名字被称为算法，实际上更准确的应该换成方法。因为我们这一节主要使用到的软件是Excel ，我们将介绍在 Excel 中绘制统计图的方法。事实上，统计图最常用的就几种：饼图、柱状图、条形图、直方图、折线图 、散点图、箱线图等。对于同一组数据，不同的同学绘制出来的效果可能截然不同，好的图形能够让读者一眼就能看出数据的规律和特点，其传递给读者的信息是准确和有效的，准确是指我们不能随意绘制图形，因为每个统计图适用的数据是有限制的；有效是指图形传递出来的信息和你得到的结论是吻合的；这是一个图形要满足的最基本两点。另外，要评价一个图形是否画的好，主要看其是否简洁和美观，我们绘制出来的图表包含的信息一定要清晰明显，不能花里胡哨，另外一定要注意图形的配色。

二、饼图

最适合采用饼图的情形：

1. 只有一个数据系列（单分类数据）。

2. 任何数据值都不为零或小于零。

3. 类别不超过七个。因为七个以上的扇区会使图表难以阅读。

4. 划分的类别最好是完整的，一般不完整时可以加其他。

5. 类别过多可用复合饼图时，千万别硬要画一个完整饼图。

6. 类别只有两个时就不用画图了，没多大必要。

注意：不用在图中加入标题，我们一般在论文的正文中加入（表上图下）。

另外，画出来的图一定要有分析，要告诉读者你画图的目的是什么。

三、柱状（形）图

3.1简述

       柱状图常常用于展示多个分类（单个分类也可以）的数据变化和同类别各变量之间的比较情况。堆积柱状图可用于比较同类别各变量和不同类别变量总和差异；百分比堆积柱状图适合展示同类别的每个变量的比例。

3.2切换行列后的柱状图 

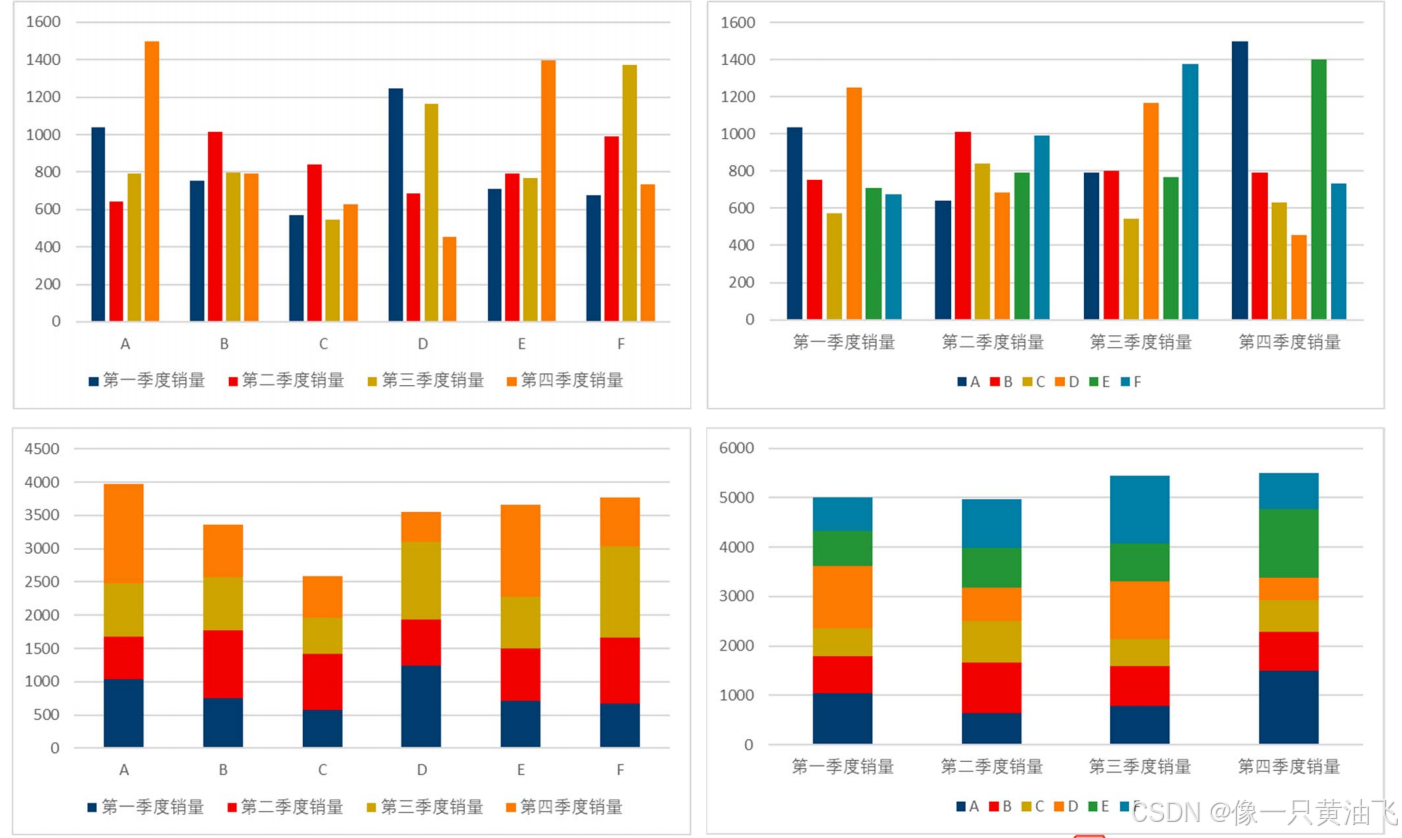
3.3用柱状图可视化回归结果

对图形的解读：

（1）用红色和黑色区分了显著和不显著的系数估计。红色是指系数估计跟0有显著差异，而黑色是指没有。因此解读的时候，关注红色柱子即可。

（2）柱子朝上，说明自变量和因变量的关系是正向的。自变量取值增加的时候，因变量取值也增加。类似地，如果柱子朝下，说明自变量和因变量的关系是负向的。自变量取值越大，因变量取值则越小。

（3）若对自变量进行了标准化，那么柱子的高度，也就是系数的估计值有可比性，可以直观地区分出自变量对因变量的影响大小。

四、条形图（横过来的柱状图） 

4.1简述

类别数过多时，如果要加入数据标签，那么使用条形图比较合适

柱状图的数看起来有点拥挤

 

4.2双向条形图 

 

五、直方图 

5.1简述

直方图是显示数据频数或频率的柱状图。

5.2直方图和柱状图的区别

       直方图（Histogram）是一种可视化在连续间隔，或者是特定时间段内数据分布情况的图表，经常被用在统计学领域。简单来说，直方图描述的是一组数据的频次分布，例如把年龄分成“0-5,5-10，……，80-85”17个组，统计一下中国人口年龄的分布情况。直方图有助于我们知道数据的分布情况，诸如众数、中位数的大致位置、数据是否存在缺口或者异常值。 （注：众数是指一组数据中出现次数最多的数据值，众数可能是一个数，但也可能是多个数。中位数是指可将数值集合划分为相等的上下两部分的数。）

       直方图和柱状图最让人迷惑的地方，就是它们长得非常相似。实 际上，直方图和柱状图无论是在图表意义、适用数据上，还是图表绘 制上，都有很大的不同。

        1. 直方图展示数据的分布，柱状图比较数据的大小。

        2. 直方图 X 轴为定量数据，柱状图 X 轴为分类数据。

        3. 直方图 y 轴要么为数据的频数，要么为数据的频率，柱状图 y 轴为数据 实际大小。

5.3组距对于直方图的影响

组距会影响直方图呈现出来的数据分布，因此在绘制直方图的时候需要多次尝试改变组距。

下图从上到下的组距分别为： 5,2,1.

5.4频数和频率分布直方图

5.4.1第一步

首先，将数据分析功能打开，打开方式见以下博客：

EXCEL中如何调出“数据分析”的菜单

5.4.2第二步 

数据分析—直方图—选择输入区域和接受区域，勾选标志后点击确定—求出出频率和区间—选中区间和频率绘制柱状图

注：

①区间除了第一个以外的规律函数：="("&A2&","&A3&"]"

注意：有的地方的频率分布直方图的纵坐标取的是频率 / 组距，大多数情况下直方图对应的各个类别组距相等，因此得到的图形和我们这里没有实质的区别，仅仅相差了一个倍数关系。

六、折线图 

6.1简述

       如果数据是时间序列数据（如日、月、季度或年度数据），则应该考虑使用折线图，尤其是时间跨度长且存在多个时间序列时，更应该使用折线图 。（折线图也经常被称为时间序列图，或简称为时序图）

       当然，时间序列期数较少时，也可以考虑使用柱状图哦。

6.2 折线图和柱状图的对比

6.3一个错误及解决

6.4双坐标轴折线图

所谓双坐标轴即有两个Y轴

原理：次坐标的图形通常在最高一层显示。

6.5 柱形图顶端的折线图

画法 

以以下数据为例子：

首先从冰箱开始，将各列数据复制到一列，为了留白各列数据之间相隔两行，后面以此类推，部分展示如下：

补充——快速复制数据的方法：

①在总数据的冰箱数据这一列隔两行，写 =C2 (C2即洗衣机这一列的第一个数据的坐标）

②在这一单元格的右下角出现的黑色十字架点击拖动到第K行

③再在这一行的右下角出现的黑色十字架点击往下拖动直到B列数据出现0为止，此时B列数据已经复制完了

④选择B列，点击数据-数据筛选-只选择0

⑤选择B列的数据，右键-清除内容

⑥点击B列的筛选-全选，得到最终所需数据：

选择冰箱这一列的数据先生成一个如下的折线图：

点击该折线图右键—选择数据—点击添加—系列名称点击冰箱，系列值选择冰箱这一列的数据—点击折线上的随便一点—右键选择更改系列图表类型—将其中一个系列选择为面积图，即得到了以下图表：

修改横坐标： 点击该图表右键选择数据—添加—系列名称随便打（我打的111），系列值要有十列—在菜单栏”格式“选择系列111，然后在设置数据系列格式-系列选项选择次坐标轴—再右键选择数据-点击”111“-编辑-选择从”冰箱“到”照相机“—图表右上角加号-坐标轴-勾选次要横坐标轴，此时图表显示如下：

为了将”冰箱-照相机“移到底部：首先点击右边次坐标轴的y轴，在设置坐标轴格式的坐标轴选项-横坐标轴交叉-选择自动，此时图表变为：

再依次点击数字的横坐标轴和次坐标轴的y轴，在设置坐标轴格式-标签-标签位置选择”无“，最终图表：

七、散点图 

7.1简述

       散点图也叫 X-Y 图，它将所有的数据以点的形式展现在直角坐标系上，以显示变量之间的相互影响程度，点的位置由变量的数值决定。

       通过观察散点图上数据点的分布情况，我们可以推断出变量间的相关性。如果变量之间不存在相互关系，那么在散点图上就会表现为随机分布的离散的点，如果存在某种相关性，那么大部分的数据点就会相对密集并以某种趋势呈现。数据的相关关系主要分为：正相关（两个变量值同时增长）、负相关（一个变量值增加另一个变量值下降）、不相关、线性相关、指数相关等，表现在散点图上的大致分布如右图所示。那些离点集群较远的点我们称为离群点或者异常点。

7.2带标识的散点图 

添加趋势线：在图表右上角的“+”号

将表格变为如下这样：

 

 

八、箱线图 

8.1简述

       箱线图也称箱须图、箱形图、盒图，用于反映一组或多组连续型定量数据分布的中心位置和散布范围。箱形图包含数学统计量，不仅能够分析不同类别数据各层次水平差异，还能揭示数据间离散程度、异常值、分布差异等等。

 计算过程（注意：箱线图有不同的画法，下面介绍的是用的较多的一种画法）：

1. 计算上四分位数、中位数、下四分位数以及均值；

2. 计算上四分位数和下四分位数之间的差值，即四分位数差（ IQR ， interquartile range ）；

3. 绘制箱线图的上下范围，上限为上四分位数，下限为下四分位数，在箱子内部中位数的位置绘制横线；

4. 大于上四分位数 1.5 倍四分位数差的值，或者小于下四分位数 1.5 倍四分位数差的值，划为异常值（ outliers ）；

5. 排除掉异常值之外，在剩下的数据的最大值和最小值处画横线，作为箱线图的上下边缘；

6. 极端异常值，即超出四分位数差 3 倍距离的异常值，用实心点表示；较为温和的异常值，即处于 1.5 倍 ‐3 倍四分位数差之间的异常值，用空心点表示；

7. 为箱线图添加名称，数轴等，并在图中用×标记出数据的均值位置。

8.2箱线图的作用 

       箱线图的用法是，配合定性变量画分组箱线图，作比较。如果只有一个定量变量，很少用一个箱线图去展示其分布，更多选择直方图。箱线图更有效的使用方法是作比较。

       假设要比较男女生的身高，用什么工具最好？答案是箱线图。箱线图明显更加有效，能够从平均水平（中位数）、波动程度（箱子高度）以及异常值对男女教师的教学评估得分进行比较，而直方图却做不到。