一、哈夫曼树定义及用途
哈夫曼树又称最优二叉树,是带权路径长度(WPL)最短的树,可以构造最优编码,用于数据传输,数据压缩等方向
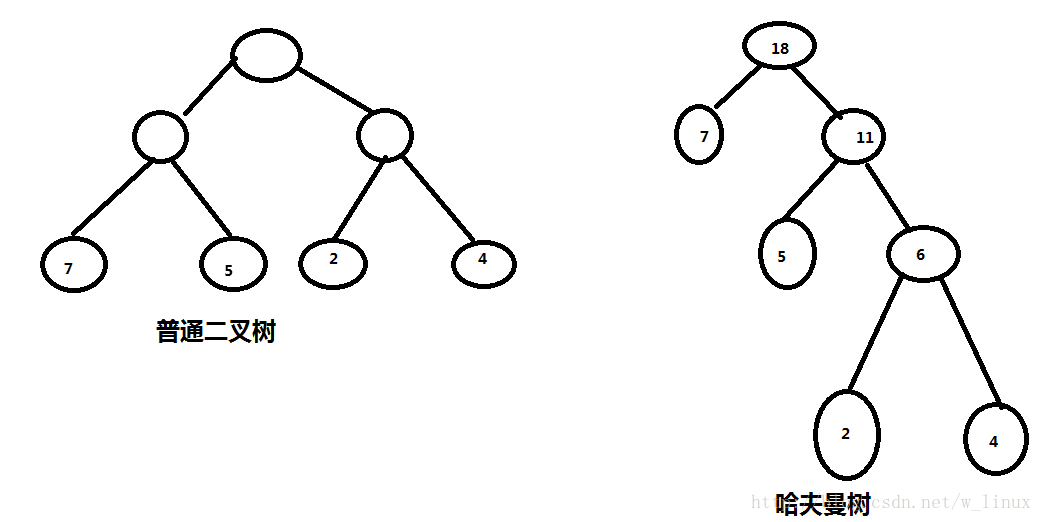
下面是二叉树和哈夫曼树
二、概念
- 路径:树中一个结点到另一个结点之间的分支序列构成两个结点间的路径
- 路径长度:路径上的分支数目
- 树的路径长度:树根到每个结点的路径长度的和
- 结点带权路径长度:结点到树根的路径长度与结点的权的乘积
- 树的带权路径长度:树中所以叶子结点的带权路径长度之和(WPL)
- 最优二叉树:在叶子个数n以及各叶子的权值确定的条件下,树的带权路径长度WPL最小的二叉树
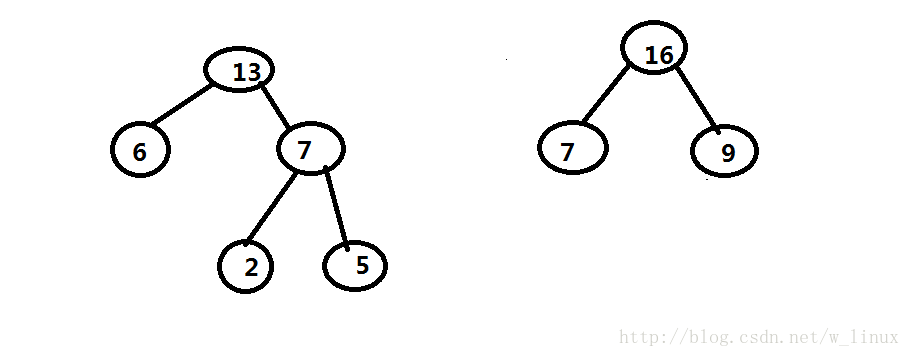
三、哈夫曼树的构造(以下举例以5,6,2,9,7森林为例)
1、根据给定的n个权值(W1,W2,W3….)构造n棵二叉树的集合F={T1,T2,T3..}其中每棵二叉树Ti只有一个带权为Wi的根结点,其左右子树为空
2、在F中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,它俩的双亲的权值是它俩权值之和(如下图出现两个7,不用担心,不管哪个7和6匹配都不会有问题)
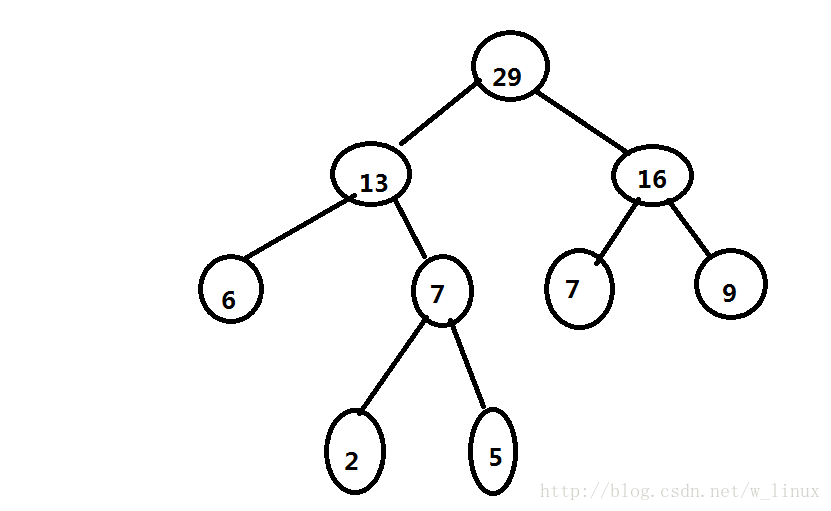
3、通过(2)得到两棵构成新的二叉树
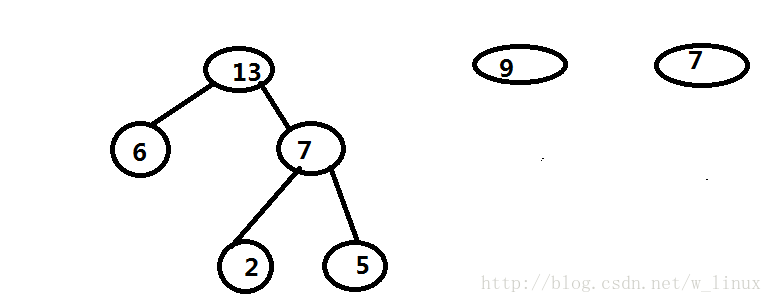
4、重复(2)(3)操作,直到最后为一棵树为止,这棵树便是哈夫曼树
四、哈夫曼编码
哈夫曼最大的目的是为了解决当你远距离通信(电报)的数据传输的最优化问题
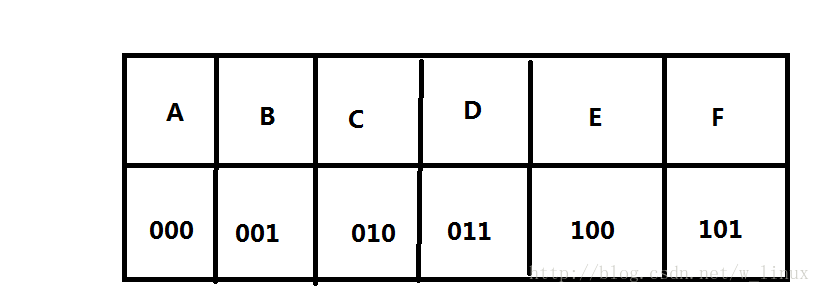
比如文字内容”ABCDEF”,通过二进制数据表示
传输数据为:“000001010011100101”按照3位一分来译码即可,但可以想象假如文字多了,数据量也是相当的大,而且某写字出现的频率都是不同的“中文的,了,….”频率大
所以需要前缀编码来进行编码(哈夫曼思想)
前缀编码:设计长短不等的编码,必须是任一字符的编码都不是另一个字符编码的前缀,这种编码称为前缀编码
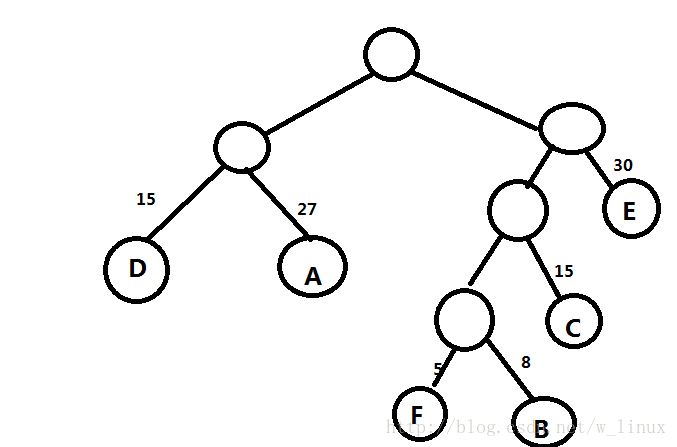
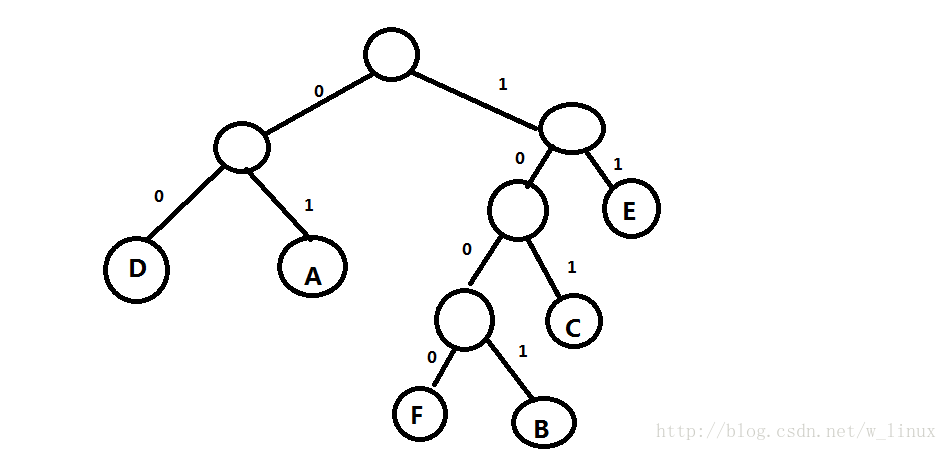
因为每个字母的出现频率是不同的,我们假设给每个字母分配权值:A:27,B:8,C:15,D:15,E:30,F:5,首先按照它们的权值进行构造哈夫曼树
将所有权值左分支改为0,右分支改为1.
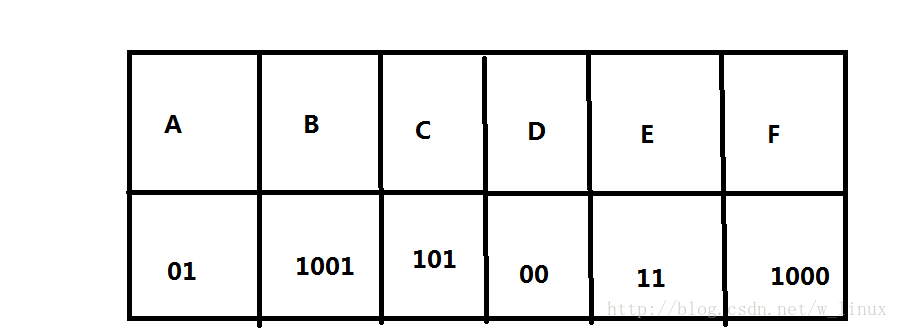
得到相应字符的的传输数据
下面是通过哈夫曼编码得到,可以看出,频率高的字符数据变的少,这样如果在很多字符下,会大大减少存储率和传输成本
- 原编码二进制串:000001010011100101
- 新编码二进制串:01100110100111000








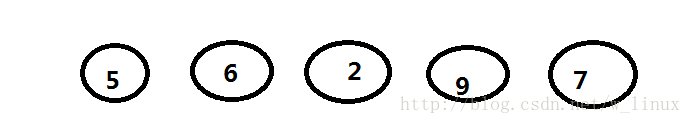
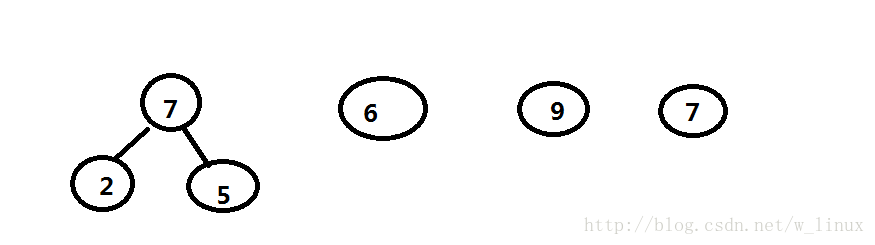
















 3425
3425

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








