【bzoj2820】YY的GCD 莫比乌斯函数

Description

神犇YY虐完数论后给傻×kAc出了一题
给定N, M,求1<=x<=N, 1<=y<=M且gcd(x, y)为质数的(x, y)有多少对
kAc这种傻×必然不会了，于是向你来请教……
多组输入
Input

第一行一个整数T 表述数据组数
接下来T行，每行两个正整数，表示N, M
Output

T行，每行一个整数表示第i组数据的结果
Sample Input

2
10 10
100 100
Sample Output

30
2791
HINT

T = 10000

N, M <= 10000000

题解

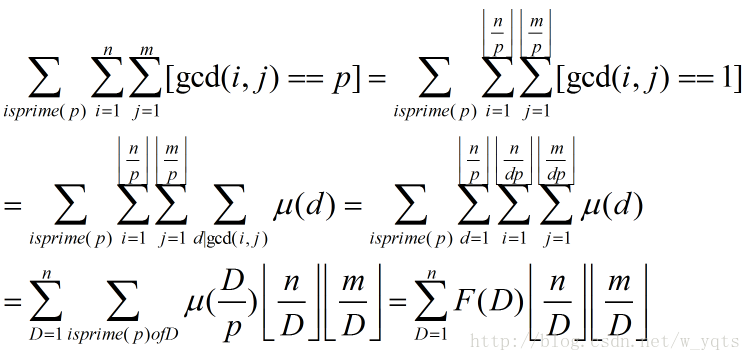
利用线性筛预处理前缀和
询问对n，m分块即可

代码

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define ll long long
#define inf 1000000000000000LL
#define mod 10000007
using namespace std;
inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
const int N=10000001;
int miu[N+2],f[N+2],p[N+2],tot,flag[N+2],n,m;
void pre()
{
    miu[1]=1;
    for (int i=2;i<=N;i++)
    {
        if (!flag[i]) p[++tot]=i,miu[i]=-1,f[i]=1;
        for (int j=1;j<=tot&&p[j]*i<=N;j++)
        {
            flag[i*p[j]]=1;
            if (i%p[j]==0)
            {
                miu[i*p[j]]=0;
                f[i*p[j]]=miu[i];
                break;
            }
            miu[i*p[j]]=-miu[i];
            f[i*p[j]]=miu[i]-f[i];
        }
        f[i]+=f[i-1];
    }
}
void solve()
{
    n=read();m=read();ll ans=0;
    for (int i=1,pos;i<=min(n,m);i=pos+1)
    {
        pos=min(n/(n/i),m/(m/i));
        ans+=1LL*(f[pos]-f[i-1])*(n/i)*(m/i);
    }
    printf("%lld\n",ans);
}
int main()
{
    pre();
    int Case=read();
    while (Case--) solve();
    return 0;
}