参数估计统计量总结

walking_visitor

于 2021-07-04 16:06:03 发布

阅读量1.8k

点赞数 1

分类专栏：统计学文章标签：统计学参数估计

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/walking_visitor/article/details/118416552

版权

统计学专栏收录该内容

8 篇文章

订阅专栏

目录

一个总体的参数的检验

总体均值的置信区间估计

总体比例的置信区间估计

总体方差的置信区间估计

两个总体的参数检验

两个总体的均值之差

两个总体的比例之差的区间估计

两个总体方差比的区间估计

一个总体的参数的检验

一般性问题有：

总体均值的置信区间估计
总体比例的置信区间估计
总体方差的置信区间估计

一个总体的参数检验需要考虑的因素有总体分布是否为正太分布、总体方差是否已知、抽样样本量是大还是小。

总结如下：

总体均值的置信区间估计

总体分布	样本量	总体标准差已知	总体标准差未知
正态分布	大于30(大样本)	$\bar{x}\pm z_{a/2}*\frac{\alpha}{\sqrt{n}}$	$\bar{x}\pm z_{a/2}*\frac{s}{\sqrt{n}}$
正态分布	小于30(小样本)	$\bar{x}\pm z_{a/2}*\frac{\alpha}{\sqrt{n}}$	$\bar{x}\pm t_{a/2}*\frac{\alpha}{\sqrt{n}}$
非正态分布	大于30(大样本)	$\bar{x}\pm z_{a/2}*\frac{\alpha}{\sqrt{n}}$	$\bar{x}\pm z_{a/2}*\frac{s}{\sqrt{n}}$

总体比例的置信区间估计

总体比例只考虑大样本情况下的估计

$p\pm z_{a/2}\sqrt{\frac{p(1-p)}{n}}$

总体方差的置信区间估计

总体方差只考虑正态总体方差的估计

$\frac{(n-1)s^{2}}{x_{a/2}^{2}}\leqslant\alpha ^{2}\leqslant \frac{(n-1)s^{2}}{x_{1-a/2}^{2}}$

两个总体的参数检验

一般性问题有：

两个总体的均值之差
两个总体的比例之差
两个总体的方差比

两个总体的均值之差

两个总体均为大样本情况下

其均值之差的抽样分布，服务期望为( $\mu _{1}-\mu _{2}$ )，方差为( $\frac{\alpha _{1}^2{}}{n1}+\frac{\alpha _{2}^2{}}{n2}$ )的正太分布，

其均值之差的置信区间估计为：

$(\bar{x1}-\bar{x2})\pm z_{a/2}\sqrt{\frac{\alpha _{1}^2{}}{n1}+\frac{\alpha _{2}^2{}}{n2}}$

当两个总体的样本方差未知时，可以用样本的方差来代替。

两个总体为小样本情况下

需要作出一些假定：

两个总体都服从正太分布

两个随机样本都抽取自独立的两个个体

在符合以上假定前提下，两个样本的均值之差都服从正太分布。

当总体方差已知时，其置信区间同大样本情况一样

当总体方差未知时，但相等时，需要用到样本方差来进行估计，这时，需要将两个样本的数据组合在一起，即总体方差估计量 $s_{p}^{2}$ ：

这时，均值之差的分布符合，自由度为(n1+n2-2)的t分布，其置信区间表达式为：

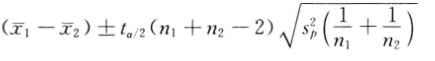
当总体方差未知，且不相等时，两个样本均值之差符合自由度为v的t分布：

其置信区间为：

两个总体的比例之差的区间估计

当两个总体的比例( $\pi _{1},\pi _{2}$ )未知时,可用样本比例代替，其比例之差的置信区间为：

两个总体方差比的区间估计

两个总体方差比服从F(n1-1,n2-2)分布，其方差比的置信区间为：

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。