EMD即Earth Mover's Distance,是2000年IJCV期刊文章《The Earth Mover's Distance as a Metric for Image Retrieval》提出的一种直方图相似度量(作者在之前的会议论文中也已经提到,不过鉴于IJCV的权威性和完整性,建议参考这篇文章)。基于一个经典的运输问题求解,作者提出的EMD距离本人看来是一个非常好的度量方式。如果想细致深入的理解,建议参考这篇论文。从网上没有搜到多少对它的通俗的解释,这里将尝试以浅显易懂的方式进行阐述,希望对大家能有所帮助。
一、基本概念解释
为了进一步讨论它的细节,首先要介绍一下signature的概念,很简单,一看就懂。
(1) 先说直方图。大家都知道,一个图像的直方图就是把图像像素值量化为一系列bin,统计落在相应bin的像素个数,就形成了直方图。
(2) signature(请恕我不知道怎么准确翻译这个词哈,只能用英文了)的定义为








 EMD,全称Earth Mover's Distance,是一种用于衡量直方图相似性的度量方法,源于2000年的IJCV论文。它通过解决线性规划问题,最小化类间转移的代价,来计算两个直方图之间的距离。直方图被转化为签名,简化表示并节省空间。EMD不仅考虑了直方图的分布,还考虑了移动成本,确保了更精确的相似度评估。
EMD,全称Earth Mover's Distance,是一种用于衡量直方图相似性的度量方法,源于2000年的IJCV论文。它通过解决线性规划问题,最小化类间转移的代价,来计算两个直方图之间的距离。直方图被转化为签名,简化表示并节省空间。EMD不仅考虑了直方图的分布,还考虑了移动成本,确保了更精确的相似度评估。
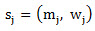
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 397
397

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








