0.1+0.2不等于0.3，IEEE754标准

0.1+0.2不等于0.3？

想要知道这个原因，我们先看一下浮点数之间计算的规则，浮点数之间进行相加时是按照IEEE 754来进行相加的，也就是它不是按照十进制相加，而是先把十进制数转化为二进制，ok，先看下面几条解释…

1). 十进制数如何转化为二进制

计算机中，所有数据都是以二进制形式存在。而十进制数转换为二进制的方法是“整数部分除以2，逆序取余；小数部分乘以2，顺序取整。

举个栗子：十进制105.625转化为二进制数为1101001.101

2). 二进制的指数形式

//任何一个十进制数D都可以表示为D=M*10^E次方。同理任何一个二进制B都可以表示为B=M*2^E次方。其中E为指数，M为B的尾数
//比如：
//十进制数105可以表示为：1.05 * 10^2
//二进制数0.00101可以表示为：1.01 * 2^-11

指数表示方式可以在有限的存储空间中表示更大的数据范围，所以计算机采用科学计数法这种指数形式存储数据。比如：

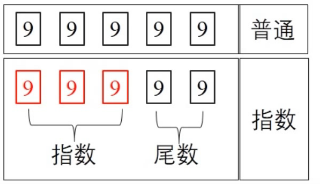
//以5位长度十进制为例，如果不采用科学计数法，5位长度构成的数字最大是99999；而如果采用科学计数法，前三位存放指数，后两位存放尾数，则可以最大表示为9.99 * 10^999

3). 浮点数IEEE 754标准

IEEE 754是现如今以来最广泛使用的浮点数（小数）运算标准，为许多CPU与浮点数运算器所采用，该标准定义了表示浮点数的格式与反常值，一些特殊数值以及这些数值的“浮点运算符”。

IEEE 754规定：第一位为符号位，1表示负数、0表示正数。接下来的11位表示指数，然后最后52位表示指数（重点）

知道了以上内容，来看为什么0.1+0.2！=0.3

• 第一步：将十进制的0.1和0.2转化为二进制

转化规则就是：整数部分除以2，逆序取余；小数部分乘以2，顺序取整。

• 第二步：将一般二进制转换成IEEE 754标准形式。

注意：这里由于不参与指数运算，这是简化的一般形式转化为指数形式。

由于指数形式依然是无无线循环小数，所以根据IEEE754规定，小数点后尾数只能保留52位，超过的位数需要丢弃掉，并且丢弃的时候看情况如果第53位是1则需要进位。

• 第三步：0.1 + 02

• 第四步：将0.1 + 0.2的二进制结果转化为十进制

二进制转化为十进制的方法是按照位权展开求和。如下：

总结来说，就是浮点数之间进行相加时是按照IEEE 754来进行相加的，也就是它不是按照十进制相加，而是先把十进制数转化为二进制，然后通过二进制转化为IEEE 754标准的方式进行相加，相加过程中小数点后仅仅保留52位数，对于无限循环的需要舍弃，所以就出现了浮点数之间相加的误差。若要在代码中解决这种误差可以采用四舍五入的方式保留两位有效数字即可解决。