位运算的一些性质

记号

位运算中的集合符号

定义x$⫅$y表示x的二进制位每一位都小于或等于y的对应位。
对于x$\subseteq$y有同样的意思。
x$\subset$y表示x$\subseteq$y且x≠y。

与运算

定义如下形式表示整数x、y做位与运算：

• x $and$ y
• x&y
• x∩y
• x $bitand$ y

或运算

定义如下形式表示整数x、y做位或运算：

• x $or$ y
• x|y
• x∪y
• x $bitor$ y

按位取反

定义如下形式表示整数x按位取反：

• $not$ x
• ~x
• $\overline{x}$

异或运算

定义如下形式表示整数x、y做位异或运算：

• x $xor$ y
• x^y
• x$\oplus$y

与运算对应交集，或运算对应并集，而取反运算对应补集。
事实上，异或运算对应集合运算中的“对称差”，有时也用$A△B$表示。

左移与右移运算

定义如下形式表示整数x、y做左移运算：

• x<<y

定义如下形式表示整数x、y做右移运算

• x>>y

位运算性质

交换律、结合律、幂等律

位与、位或、位异或运算具有交换律和结合律。

• x∩y=y∩x，x∩(y∩z)=(x∩y)∩z
  所有与运算数，在同一位上有一个为0，这一位最终结果就是0；
• x∪y=y∪x，x∪(y∪z)=(x∪y)∪z
  所有或运算数，在同一位上有一个为1，这一位最终结果就是1；
• x$\oplus$y=y$\oplus$x，x$\oplus$(y$\oplus$z)=(x$\oplus$y)$\oplus$z
  所有异或运算数，在同一位上1的个数为奇数，这一位最终结果就是奇数。

事实上，由于位运算各个数位之间是独立的，所以只需要证明同一个二进制位中定理成立，就可以证明定理成立。
因此所有定理都可以通过分情况讨论得出，因此下面就不证明了，直接给出结论。

此外：

• x∩x=x
• x∪x=x
• x$\oplus$x=0
  显然.

分配律

位运算满足对应的集合运算分配律：

• x∩(y∪z)=(x∩y)∪(x∩z)
• x∪(y∩z)=(x∪y)∩(x∪z)

异或运算和与运算也满足分配律：

• x∩(y$\oplus$z)=(x∩y)$\oplus$(x∩z)
  有的地方称这个为“分段律”

一个错误的例子：
x$\oplus$(y∩z)=(x$\oplus$y)∩(x$\oplus$z)

这表明与运算、异或运算可以拆开。

吸收律

位运算满足对应的集合运算的吸收律。

• x∪(x∩y)=x
• x∩(x∪y)=x

有的地方说位异或运算满足吸收律，例如：A∩(A$\oplus$B)=A或者A∪(A$\oplus$B)=B。
但这事实上是错的，位异或运算不满足吸收律。

其他定律

位运算还满足其他一些对应的集合运算定律，例如对合律：$\overline{\overline{x}}=x$。
其他过于简单的定律不再赘述。

位运算事实上还满足对应集合运算的德·摩根定律：

• $\overline{x\cap y}=\overline{x}\cup \overline{y}$
• $\overline{x\cup y}=\overline{x}\cap \overline{y}$

上述所有二元定律的多元形式，位运算有对应的满足。

异或运算事实上还满足：
x$\oplus$y=(x∩y)$\oplus$(x∪y)
由于异或运算、或运算拆不开，因此该公式似乎没有多元形式。

lowbit、highbit

lowbit(x)表示x的二进制表示中最低位的1代表的值。
如：lowbit(4)=4，lowbit(3)=1

• $lowbit(x)=x\cap -x$
  也就是lowbit(x)=x&-x

highbit(x)表示x的二进制表示中最高位的1代表的值。
如：highbit(5)=4

highbit没什么太好的求法，不过主流来说有这么两种方法：

1. 大致原理就是作差：
   
   2.还可以用builtin函数：
   
   不过注意不同类型builtin函数名不一样。

还有一种做法是不断地减去lowbit，不过这个太慢了，不考虑。

事实上还有：

• x∩-x=lowbit(x)
• x∪-x=-lowbit(x)
• x$\oplus$-x=-lowbit(x)<<1
  x可以是负数。

位运算技巧

异或和

归纳法易证：
${⨁}_{i=1}^{n}i=\{\begin{array}{c}n\equiv 0(mod4):n\\ n\equiv 1(mod4):1\\ n\equiv 2(mod4):n+1\\ n\equiv 3(mod4):0\end{array}$

与和、或和按位判一下就行。

__builtin函数

__builtin函数用于位运算，在algorithm库内。
__builtin函数虽然不是c++标准，但是比赛的GNU还是支持这个东西的。

• 统计前导零（count leading zero）：__builtin_clz(x)
• 统计后缀零（count trailing zero）：__builtin_ctz(x)
• 统计二进制位中1的个数(popcount)：__builtin_popcount(x)
• 快速开平方：__builtin_sqrtl(x)
  参数是long double
• 快速开平方：__builtin_sqrt(x)
  参数是double
• 快速开平方：__builtin_sqrtf(x)
  参数是float
  因为启用了硬件加速，可能比直接sqrt快很多。
  也可能只有一个递归的差距，毕竟：

其他一些用处不是很大的__builtin函数

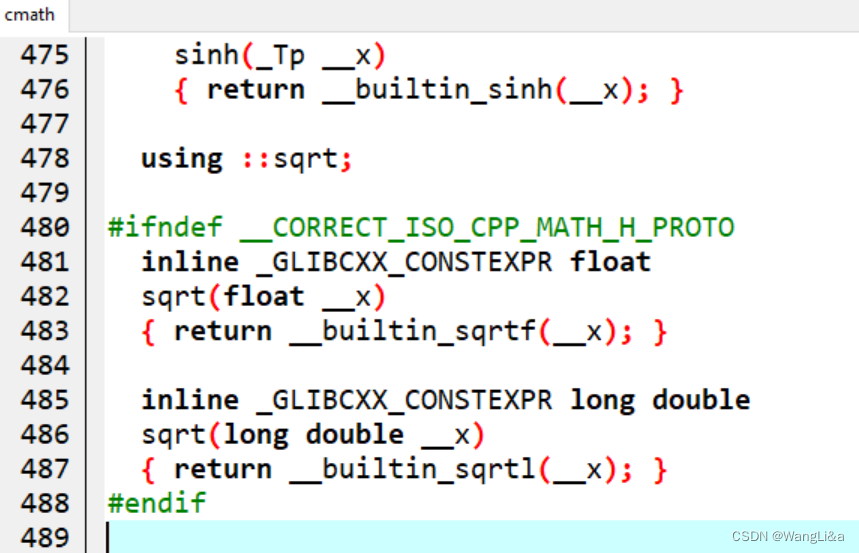
注意__builtin函数在longlong和long有其对应形式：
如前导零函数：
unsigned:__builtin_clz(x)
unsigned long:__builtin_clzl(x)
unsigned long long:__builtin_clzll(x)

后记

于是皆大欢喜。