容斥dp，二项式反演

前言

由于水平有限，这篇文章比较难懂，并且也有很多不够透彻的地方，如果您有任何的看法，非常感谢您私信指导。

容斥dp

用dp的方法来描述容斥，大概的想法是，把容斥系数分到每一步里去乘。

通常当你有容斥做法，且适配的子集条件较为一般，且数据范围不足通过时考虑使用容斥dp。

确实不太好描述，看题吧。

来源神秘

求长度为$n\le 2000$，值域为$m\le 2000$的序列个数，满足前一个数不是后一个数的非本身的倍数。

设$f_{i,j}$表示前$i$个数，第$i$个数为$j$的合法序列方案数，则：
$f_{i,j}=\underset{k=1}{\sum ^m}[j=k或j\nmid k]f_{i-1,k}$
复杂度$O(n{m}^2)$

如果我们转化成：
$f_{i,j}=\underset{k=1}{\sum ^m}{f}_{i-1,k}-\underset{k=1}{\sum ^m}[j\ne k且j\mid k]f_{i-1,k}$

就可以做到$O(nm\log m)$

$n,m\le 10^5$：
考虑容斥，如果设$S_i$表示第$i,i+1$个数满足限制的所有方案构成的集合，那么答案为$|\bigcap S_i|$，那么其补集为一些数不满足限制，也就是说是倍数关系。如果设$f(i)$表示$i$选出$i$个位置不满足条件的方案数，设$g(i)$表示恰好$n$中有$i$个位置不满足条件的方案数，那么相当于二项式反演的式子（虽然可以直接认为是容斥，但是虽然但是）：
$f(x)=\underset{i=x}{\sum ^n}\left(\begin{array}{c}i\\ x\end{array}\right)g(i)$
$g(x)=\underset{i=x}{\sum ^n}\left(\begin{array}{c}i\\ x\end{array}\right)(-1{)}^{i-x}f(i)$
$ans=g(0)=\underset{i=0}{\sum ^n}(-1{)}^{i}f(i)$

我们可以认为一个不合法的相邻位置会贡献一个$-1$的容斥系数，具体来说会给它这种方案乘上一个$-1$的系数，对于一种方案来说，它实际上对答案的贡献（加到答案上的值是）$(-1{)}^k$，其中$k$表示这种方案中有多少邻居不合法。

然后我们考虑现在的所有位置，存在着两种情况，一种叫做“非法”，一种叫做“不管”，这些东西形成了一些连续段，最终拼成了整个序列。

那么可以将数列拆成 $1$个不知道+$x\ge 0$个非法 的若干连续段，相当于编出来一个转移。

那么就可以根据这个东西把序列划分为若干个阶段，然后设出状态。即$f_i$表示以$i$为结尾的所有容斥系数之和。容易发现$f_i$等于长度为$i$的合法序列的数量。

那么就会有$f_i=\sum _{j\ge 0}{f}_{i-j}\cdot w_j\cdot h(j)$，相当于枚举最后一个非法段的长度。
那么$h(j)=(-1{)}^{j-1}$，因为长度为$j$的非法段其实指定了$j-1$个非法位置，以及开头有一个不管的位置。

$w_j$表示长度为$j$的非法段共有多少种，容易发现这种段的长度为$\log m$

这样可以做到$O((n+m)\log m)$

$n\le 10^{18},m\le 10^6$：
转移与前面$\log m$项有关，可以矩阵加速。
$O({\log }^{3}m\log n+m\text{poly}\log m)$

$n\le 10^{18},m\le 10^9$：配合各类筛法以及根号分治。

AT_dp_y/CF599C

不能走黑不好做。考虑容斥，设$S_i$表示第$i$个黑色格子不走的方案数，则$ans=|\bigcap S_i|$，其补集转化为走一些黑色格子。

设$f(x)$表示选出$x$个黑走的方案数，则$ans=\underset{i=0}{\sum ^n}(-1{)}^{i}f(i)$

我们先把黑色格子以$(x,y)$升序排列，然后设$f_i$表示必然走第$i$个黑格子的所有方案的系数和，在这里会发现这实际上相当于以第$i$个黑格子为终点，其他黑色格子不走的方案数。

那么转移就是$f_i=\sum _{j<i}-\left(\begin{array}{c}{x}_i-x_j+y_i-y_j\\ x_i-x_j\end{array}\right)f_j$，表示枚举之前走了哪个黑色格子。
这里的$-1$是因为当前走了一个黑色格子，所以要乘上$-1$的系数。
组合数是表示从上一个黑色格子走到这里的方案数。

这样会发现一个问题是，这样没有办法表示是从左上角出发，到右下角结束的。因此我们强制在左上角和右下角添加一个黑色格子。并且令初值$f_1=-1$，表示走了左上角黑色格子的方案容斥系数和。

观察转移的形式，我们会发现$f_i$实际上表示的是走了左上角那个黑色格子，以及第$i$个黑色格子的方案数，这样就可以做了。

时间复杂度$O(n^2)$

CF1728G

标算做法是由于每次只添加一盏灯，因此会照亮一个连续段，只需要剩下的灯照亮前后缀即可，预处理前后缀就能算出来。

但是有多项式做法。

考虑容斥是怎么做的，相当于选出一些点强制不能照亮，剩下点随意，这样方案数是好求的。
那么对于一种照亮的情况，我们可以把它划分为 首尾不能照亮+中间随意的连续段，那么设$f_i$表示第$i$个点为结尾的容斥系数和，转移相当于枚举最后一个左右为不能照亮，中间是任意的连续段。（以$i$为结尾，说明$i$不能照亮）

那么$f_i=\sum _{j<i}-w_{j,i}\cdot f_j$

$w$是$O(n{m}^2)$好算的。

这样dp出来相当于强制第一个点和第$i$个点不能照亮的方案数，所以我们在正负无穷的位置添加两个点，就可以dp出答案。

这样每次询问$w$只会有$m^2$个位置（在这次询问中）改变。

复杂度为$O((n+q)m^2)$

填数（模拟赛题）

给定 $n,m,k$ 和 $k$ 个区间 $(l_i,r_i)$，求有多少个长为 $n$ 的正整数数组 $a$ 满足：

1. $1\le a_i\le m$。
2. 对于每个给定的区间 $(l_i,r_i)$，存在至少一对 $l_i\le p_0<p_1\le r_i$，满足 $a_{p_0}=a_{p_1}$。

答案对 $10^9+7$ 取模。$1\le n,m\le 10^6$，$1\le k\le 2000$。

区间问题一个经典套路是不存在相交区间或者不存在包含区间。
本题中我们发现子集严格强于超集，因此不存在包含区间。我们把包含区间去重之后编一个后效性消除，把区间按照右端点升序排列。

然后我们把$=$容斥为$\ne$，相当于强制一些区间当中没有重复的数字，然后用dp的方法把容斥系数乘起来。

设$f_i$表示考虑前$i$个区间，第$i$个区间被选为非法的所有情况的容斥系数和，则：

$f_i=\sum _{j<i}-f_j\cdot \{\begin{array}{c}{l}_i>r_j:m^{\underline{le{n}_i}}\cdot m^{l_i-r_j}\\ else:(m-(r_j-l_i+1){)}^{\underline{le{n}_i-(r_j-l_i+1)}}\end{array}$

强制开头结尾有一个区间即可。

P4099

首先这个题有不容斥的做法，如果设$f_u$表示以$u$为子树的答案会发现没法转移，因为不知道子树内部拓扑序的情况。
如果我们想要把一个儿子加入，必须要知道这个儿子在拓扑序列中的排名，因此必须要记录进状态里，即$f_{u,i}$表示以$u$为子树，$u$在拓扑序列中的顺序为$i$的方案数。然后编一个转移就可以了。

但是这个题也可以容斥（虽然容斥做法好像更难一点…）

具体来说，一条边其实提供了一个限制，即$u\to v$说明$u$的拓扑序在$v$之前，如果只有内向边是好做的，那我们选择对外向边容斥。
设$S_i$表示满足所有内向边的限制和第$i$条外向边限制的所有序列构成的集合，则答案为$|\bigcap S_i|$，那么补集相当于取到一些外向边，然后把它们反转为内向边，剩下一些外向边断开的方案数。

那么如果我们指定一个反转，可以认为那条外向边带有$-1$的容斥系数。

非常容易编出来一个dp，即$f_u$表示$u$子树的答案，转移考虑把$u$的一个儿子合并到$u$子树内部，如果是内向边，就乘上$\left(\begin{array}{c}si{z}_u+si{z}_v-1\\ si{z}_v\end{array}\right)$合并，表示$u$为最后一个节点，前面$si{z}_u+si{z}_v-1$个位置选出$si{z}_v$个位置放置$v$子树内部的拓扑序列情况。
如果是外向边，那么就考虑两种情况。
一种叫做反转，这时候带有$-\left(\begin{array}{c}si{z}_u+si{z}_v-1\\ si{z}_v\end{array}\right)$的系数。
另一种叫做断开，这时候带有$\left(\begin{array}{c}si{z}_u+si{z}_v\\ si{z}_v\end{array}\right)$的系数，因为与$u$没有关系了，$u$不一定是最后一个，因此可以在任意位置插入。

void dfs(int u,int fa) {
	f[u]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		dfs(v,u);
		if(w) f[u]=f[u]*f[v]%M*C[siz[u]+siz[v]-1][siz[v]]%M;
		else f[u]=f[u]*f[v]%M*C[siz[u]+siz[v]-1][siz[v]-1]%M;
		siz[u]+=siz[v];
	}
}

但是会发现这样是错的。

具体错误是，假如说要合并一个子树，并且一种情况经过了断边/反转之后$u$的连通块大小实际上为$x$，$v$的连通块大小为$y$，但是我们在合并内向边的时候强制$u$在最后一个，即从$si{z}_u+si{z}_v-1$中选，实际上是不对的，我们只需要强制在$x+y$个位置中，$u$在最后一个即可。那我们可以修改一下状态，即设$f_{u,x}$表示目前所在的内向连通块大小为$x$的方案数，现在再来编一下转移：

• 内向边：$f_{u,x+y}\leftarrow +f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ x+y\end{array}\right)\left(\begin{array}{c}x+y-1\\ y\end{array}\right)$，表示先选出拓扑序列的一些位置放连通块，然后再连通块内部安排放置顺序，在放连通块的位置内部安排顺序时，必须强制$u$在最后一个位置。
• 外向边取反：$f_{u,x+y}\leftarrow -f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ x+y\end{array}\right)\left(\begin{array}{c}x+y-1\\ y\end{array}\right)$
• 外向边断开：$f_{u,x}\leftarrow +f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ si{z}_v\end{array}\right)$

void dfs(int u,int fa) {
	f[u][1]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		
		dfs(v,u);
		
		memset(g,0,sizeof g);
		
		for(int i=1;i<=siz[u];i++)
			for(int j=1;j<=siz[v]&&i+j<=n;j++)
				if(w)
					(g[i+j]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][i+j]%M*C[i+j-1][j]%M)%=M;
				else
					(g[i]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M,
					(g[i+j]+=(M-1)*f[u][i]%M*f[v][j]%M*C[siz[u]+siz[v]][i+j]%M*C[i+j-1][j]%M)%=M;
		
		memcpy(f[u],g,sizeof g);
		siz[u]+=siz[v];
	}
}

但是这样会发现连样例都过不了。原因是系数乘错了。乘错的原因是，在$f_{u,x}$中，已经乘上了$\left(\begin{array}{c}si{z}_u\\ x\end{array}\right)$作为大小为$x$的连通块放在$si{z}_u$个位置的方案，然后在转移到$f_{u,x+y}$时又选了一次，这样就选多了。事实上只需要在$si{z}_u+si{z}_v$个位置中选出$si{z}_v$个位置放新子树的拓扑序信息即可。但是这样就没法限制$v$在$u$前了，具有后效性，而增加一维状态记录$u$在拓扑序中的位置，来消除后效性在时间上是不可能的，因此我们选择推迟后效性。

转移：

• 内向边：$f_{u,x+y}\leftarrow +f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ si{z}_v\end{array}\right)$，表示先选出拓扑序列的一些位置放连通块，然后再连通块内部安排放置顺序，在连通块内部安排顺序时，未强制$u$在最后一个位置。
• 外向边取反：$f_{u,x+y}\leftarrow -f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ si{z}_v\end{array}\right)$
• 外向边断开：$f_{u,x}\leftarrow +f_{u,x}{f}_{v,y}\left(\begin{array}{c}si{z}_u+si{z}_v\\ si{z}_v\end{array}\right)$

注意是先合并再修改$f$，具体看代码。

当我们把$u$的所有子树合并完成之后，考虑一个实际上大小为$x$的连通块，其中由于我们并没有限制$u$必须要在其他节点之前，因此答案会多算$x$倍，因此再除掉就可以了：
$f_{u,x}\leftarrow f_{u,x}\cdot \frac{1}{x}$

#include<iostream>
#include<cstring>
#include<vector>
#include<map>
#include<numeric>
using namespace std;
const int N=1e3;
const long long M=1e9+7;
long long C[N+5][N+5];
long long f[N+5][N+5];
long long g[N+5];
long long siz[N+5];
long long inv[N+5];
vector<vector<pair<int,int>>>a;
int n;
void dfs(int u,int fa) {
	f[u][1]=1;
	siz[u]=1;
	for(auto&i:a[u]) {
		int w=i.first,v=i.second;
		if(v==fa) continue;
		
		dfs(v,u);
		
		memset(g,0,sizeof g);
		
		for(int i=1;i<=siz[u];i++)
			for(int j=1;j<=siz[v]&&i+j<=n;j++)
				if(w)
					(g[i+j]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
				else {
					(g[i]+=f[u][i]*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
					(g[i+j]+=(M-1)*f[u][i]%M*f[v][j]%M*C[siz[u]+siz[v]][siz[v]]%M)%=M;
				}
		
		memcpy(f[u],g,sizeof g);
		siz[u]+=siz[v];
	}
	for(int i=1;i<=siz[u];i++)
		(f[u][i]*=inv[i])%=M;
}
int main() {
	for(int i=0;i<=N;i++) C[i][i]=C[i][0]=1;
	inv[0]=inv[1]=1;
	for(int i=2;i<=N;i++) (inv[i]=(M-1)*(M/i)%M*inv[M%i])%=M;
	for(int i=1;i<=N;i++)
		for(int j=1;j<=N;j++)
			(C[i][j]=C[i-1][j-1]+C[i-1][j])%=M;
	int T;
	cin>>T;
	while(T--) {
		memset(f,0,sizeof f);
		memset(siz,0,sizeof siz);
		a.resize(0);
		cin>>n;
		a.resize(n+5);
		for(int i=1,u,v;i<n;i++) {
			char c;
			cin>>u>>c>>v;
			u++;
			v++;
			if(c=='<') a[u].push_back({0,v}),a[v].push_back({1,u});
			else a[u].push_back({1,v}),a[v].push_back({0,u});
		}
		dfs(1,0);
		cout<<accumulate(f[1]+1,f[1]+n+1,0ll)%M<<endl;
	}
}
/*
1
4
1 < 0
2 < 0
3 < 0

1 
3
0 < 1
0 < 2

1
4 
0 < 1 
0 < 2 
0 < 3

*/

ARC101_C

树上任意一边都被覆盖，容斥为选出一些边不被覆盖，每选出这样一条边，就在这种方案上乘一个$-1$的系数。

考虑一个dp，再合并完所有子树之后，如果我们要断开它与父亲的那条边，那就要求出子树内部随意匹配的方案数，显然与子树连通块的大小有关，因此要记录一维表示子树连通块的大小。

设$f_{u,i}$表示以$u$为根的子树目前有大小为$i$的不知道边构成的连通块的方案数，转移就是考虑把儿子$v$合并进来：

$f_{u,x+y}\leftarrow +f_{u,x}{f}_{v,y}(x>0,y\ge 0)$

先合并再修改。

如果$u$和父亲的连边是断开的，那么$u$父亲边的状态是“非法”，不是“未指定”，因此不知道连通块的大小为$0$，则$f_{u,0}$表示断边的容斥方案数，我们dp求出$f_{u,x>0}$后考虑求出$f_{u,0}$

那么$f_{u,0}\leftarrow -f_{u,i}{w}_i$，表示我们指定它向父亲的连边是断开的，因此带有$-1$的系数。
$w_i$表示大小为$i$的连通块任意匹配方案数，显然$w_{奇数}=0$，现在考虑偶数是如何递推的。

我们想要从$w_{i-2}$递推到$w_i$，那么就需要增加一对匹配，可以选择新增一对匹配，这样方案数是$1$，或者选择新增两个点，然后断开原来的$\frac{i-2}{2}$组中的一组匹配，新的两个点和旧的两个点形成两组匹配，这样配对会有$2$种方案，这样方案数是$2\left(\frac{i-2}{2}\right)=i-2$

因此$w_i=(1+i-2)w_{i-2}=(i-1)w_{i-2}$

或者得到$w_i=\underset{j=1}{\prod ^{j/2}}(2j-1)$，表示每次选出最小的点进行匹配。
初值为$f_{u,1}=1$，答案为$-f_{1,0}$，因为转移的时候假设根节点连向父亲的边断开了，所以乘了一个$-1$的系数，要再乘回来。

#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int N=5e3;
const long long M=1e9+7;
vector<int> a[N+5];
long long w[N+5];//i对
long long f[N+5][N+5];
int siz[N+5];
int n;
long long g[N+5];
void dfs(int u,int fa) {
	siz[u]=1;
	for(auto&v:a[u])
		if(v^fa) {
			dfs(v,u);
			memset(g,0,sizeof g);
			for(int x=1; x<=siz[u]; x++)
				for(int y=0; y<=siz[v]; y++)
					if(x+y<=N)
						(g[x+y]+=f[u][x]*f[v][y])%=M;
			memcpy(f[u],g,sizeof f[u]);
			siz[u]+=siz[v];
		}
	for(int i=0; i<=n; i++)
		(f[u][0]+=(M-1)*f[u][i]%M*w[i]%M)%=M;
}
int main() {
	cin>>n;
	for(int i=1,u,v; i<n; i++) {
		cin>>u>>v;
		a[v].push_back(u);
		a[u].push_back(v);
	}
	w[0]=1;
	for(int i=2; i<=n; i+=2) w[i]=w[i-2]*(i-1)%M;

	for(int i=1; i<=n; i++) f[i][1]=1;
	dfs(1,0);

//	for(int i=1;i<=n;i++,cout<<endl)
//		for(int j=0;j<=n;j++,cout<<' ')
//			cout<<f[i][j];
	cout<<(M-1)*f[1][0]%M;
}

话说不知道为啥初值设为$-1$也能过，有人知道请您联系我。

有标号连通图计数

求$n$个节点的无向连通图有多少个，节点有标号，编号为 $[1,n]$
$n<=5000$

这个题是朴素容斥，即考虑如何用容斥原理来修正答案。

设$f_i$表示大小为$i$的连通图数量，一个想法是首先连出一棵树，但是不太好搞，考虑补集转换，总边数为$\frac{i(i-1)}{2}$，总可能性为$h(i)=2^{\frac{i(i-1)}{2}}$种，减去不连通的情况即可，那我们枚举$1$号点所在的连通块大小$j$，然后从剩下的$i-1$个点中选出$j-1$个点，情况数量为：$f_j\left(\begin{array}{c}i-1\\ j-1\end{array}\right)$，剩下$i-j$个点随意连边，转移方程为：
$f_i=h(i)-\sum _{j<i}{f}_j\left(\begin{array}{c}i-1\\ j-1\end{array}\right)h(i-j)$

有标号DAG计数

求出$n$个点有标号DAG有多少个，$n<=5000$

设$f_i$表示$i$个点的有标号DAG数量。

考虑如何递推，DAG里面比较好说的要么是0入度点，要么是0出度点。我们可以指定$j$号点是零入度点，然后把其他点连边的可能性算出来就行了。但是注意到这样限制不好的，因为可能在指定$x$为零入度点的时候，$j$也是零入度点，这样就算重了。

可以想到容斥，选出$k$个零入度点的贡献就是$f(k)=\left(\begin{array}{c}i\\ k\end{array}\right)2^{k(i-k)}{f}_{i-k}$

但是这样还是不对的，具体来说，设$g(x)$表示大小为$i$的DAG中，恰好有$x$个零入度点的方案数，由于任意组合都会贡献，因此$f(x)=\underset{j=x}{\sum ^i}\left(\begin{array}{c}j\\ x\end{array}\right)g(j)$，则$g(x)=\underset{j=x}{\sum ^i}\left(\begin{array}{c}j\\ x\end{array}\right)(-1{)}^{j-x}f(j)$

然后令$f_i=\underset{x=0}{\sum ^i}g(x)$？化简完会得到$f_i=f_i$？

注意到$g(0)$表示选出$0$个零入度点的方案数，$g(0)$是$f_i$到$f_i$的转移，所以把$g_0$这一项删掉。
这也是有实际意义的，我们一开始枚举$j$作为$0$入度的点的方案数，因此我们后面改成枚举集合时，集合大小至少为$1$。

$f_i=\underset{x=1}{\sum ^i}g(x)=\underset{x=1}{\sum ^i}\underset{j=x}{\sum ^i}\left(\begin{array}{c}j\\ x\end{array}\right)(-1{)}^{j-x}\left(\begin{array}{c}i\\ j\end{array}\right)2^{j(i-j)}{f}_{i-j}=\underset{j=1}{\sum ^i}\left(\begin{array}{c}i\\ j\end{array}\right)2^{j(i-j)}{f}_{i-j}\underset{x=1}{\sum ^i}\left(\begin{array}{c}j\\ x\end{array}\right)(-1{)}^{j-x}$
$=\underset{j=1}{\sum ^i}\left(\begin{array}{c}i\\ j\end{array}\right)2^{j(i-j)}{f}_{i-j}\left(-(-1{)}^j+\underset{x=0}{\sum ^i}\left(\begin{array}{c}j\\ x\end{array}\right)(-1{)}^{j-x}\right)=\underset{j=1}{\sum ^i}\left(\begin{array}{c}i\\ j\end{array}\right)2^{j(i-j)}{f}_{i-j}\left((-1{)}^{j+1}+[j=0]\right)=\underset{j=1}{\sum ^i}\left(\begin{array}{c}i\\ j\end{array}\right)2^{j(i-j)}{f}_{i-j}(-1{)}^{j+1}$

这样就把容斥系数推出来了，当然容斥系数也可以猜出来。

这样是$O(n^2)$的。

有标号弱连通DAG计数

同上一题，区别就是要求弱连通。

容斥，枚举$1$所在的弱连通块的大小。则答案为$f_n-\underset{i=1}{\sum ^{n-1}}{f}_i{f}_{n-i}$

山东省队集训

给定一张$n\le 15$个点$m\le 200$条边的无向图，对于所有$k$ ，请求出保留恰好$k$条边使得整张图连通的方案数。

容斥，设$f_{i,S}$表示保留了$i$条边，使得$S$连通的方案数。不连通就枚举$1$所在的连通块。
$f_{i,S}=\left(\begin{array}{c}cn{t}_S\\ i\end{array}\right)-\sum _{1\in T⊊S}\underset{j=0}{\sum ^i}{f}_{j,T}\left(\begin{array}{c}cn{t}_{S-T}\\ i-j\end{array}\right)$

$cn{t}_S$表示两端都在$S$内的边的数量，时间复杂度$O(3^n{m}^2)$，难以通过。

观察到转移系数只与$cn{t}_{S-T}$有关，把$cnt$相同的$T$一起转移，复杂度$O(3^{n}m+2^n{m}^3)$，可以通过：
$f_{i,S}=\left(\begin{array}{c}cn{t}_S\\ i\end{array}\right)-\underset{k=0}{\sum ^i}\underset{j=0}{\sum ^i}\left(\begin{array}{c}k\\ i-j\end{array}\right)\times g_j(S,k)$

其中$g_i(S,k)=\sum _{1\in T⊊S}[cn{t}_{S-T}=k]f_{i,T}$

我们枚举一个$S,T,i$，把它贡献到对应的$g$上即可。

或者把$f_i$看成多项式的形式，那么就是$(1+x{)}^{?}$的形式，那我们令$(1+x)=y$，转移就变成了多项式平移，可以$O(m)$完成。

或者还有一种我没看懂的做法：
（来自lyp的PPT）





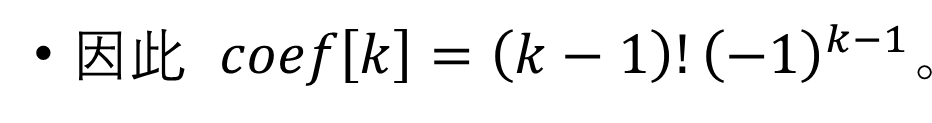
没有看懂，如果您看懂了的话，请您联系我。

LOJ575

首先想到的是离散dp。
考虑如果我们要往序列后面添加一个数字，那么我们只需要知道原来的序列末尾在序列中的排名，就可以知道我们能添加多少个比它小/大的数字了。

设$f_{i,j}$表示长度为$i$的序列值域为$[1,i]$，末尾为$j$的方案数，如果是小于号，那么$f_{i,j}(n-j+1)+\to f_{i+1,k>j}$，表示我们向$[1,i]$中插入一个比$j$大的数字$k$，把值域变为$[1,i+1]$，大于号同理。

但是这样$O(n^2)$到顶了。

考虑容斥，我们对大于号容斥，那么一些大于号会变成小于号，另一些会变成不知道。
那么符号序列就可以拼成一个不知道+若干个非法。

$f_i$表示dp到了第$i$个数字的系数和，转移就是枚举最后一个上升序列是$(j,i]$，同时要求$a_j=‘>’$，表示$a_j$被我们容斥为了不知道：
$f_i=\sum _{j<i}[a_j=‘>’](-1{)}^{cn{t}_{i-1}-cn{t}_j}{f}_j\left(\begin{array}{c}i\\ j\end{array}\right)$

时间复杂度$O(n^2)$

做分治NTT即可优化到$O(n{\log }^{2}n)$

ABC236Ex

如果到图上考虑，相等连边，那么合法方案数就是图全部不连通的方案数。

设$S_i$表示第$i$条边不存在的方案集，则要求的就是$|\bigcap S_i|$，补集就是指定一些边存在，另一些边不知道。

那么可以对边集容斥，就获得了$O\left(2^{\frac{n(n-1)}{2}}\right)$的做法。

相当于我们把点集$[n]$划分为若干集合 { S 1 , S 2 , S 3 , . . . , S k } \{S_1,S_2,S_3,...,S_k\} {S1​,S2​,S3​,...,Sk​}，确保内部连通，外部不知道。

设$f_S$表示考虑$S$内部的容斥系数之和。转移就是枚举最后一个被选出的连通块。
$f_S=\sum _{u\in T\subseteq S}{w}_T\cdot h^{\prime }(T)\cdot f_{S-T}$

那我们只需要知道$h^{\prime }(T)=h(|T|)$即可，那就是使得$|T|$个点的图连通的所有方案的容斥系数之和。

可以通过一个打表小容斥求出：
$n$个点的所有方案的容斥系数和为，枚举实际上选了几条边，得到：
$H(n)=\underset{i=0}{\sum ^{\frac{n(n-1)}{2}}}\left(\begin{array}{c}\frac{n(n-1)}{2}\\ i\end{array}\right)(-1{)}^i=[n=1]$

那么它等于连通+不连通的系数和，如果不连通，那么枚举1所在的连通块大小：
$H(n)=h(n)+\underset{i=1}{\sum ^{n-1}}\left(\begin{array}{c}n-1\\ i-1\end{array}\right)h(i)H(n-i)=h(n)+\underset{i=1}{\sum ^{n-1}}\left(\begin{array}{c}n-1\\ i-1\end{array}\right)h(i)[n-1=i]$

即：$[n=1]=h(n)+(n-1)h(n-1)$

则：$h(n)=[n=1]-(n-1)h(n-1)$

就可以做了。

但是话说这个集合划分容斥和斯特林反演什么的有啥关系，不知道，也没有查到。如果有人知道，请您私信告诉我。

后记

作者水平不行，如果您对文中问题有任何见解，非常感谢您的私信指导！