椭圆曲线密码算法概述

最新推荐文章于 2025-04-06 00:15:00 发布

立志成为网安大牛

最新推荐文章于 2025-04-06 00:15:00 发布

阅读量1k

点赞数 21

文章标签：算法

本文链接：https://blog.csdn.net/wangluoanquan111/article/details/135173129

版权

椭圆曲线密码算法

椭圆曲线密码算法（Elliptic Curve Cryptography,ECC）是基于椭圆曲线数学的一种公钥密码算法，其安全性依赖于椭圆曲线离散对数问题的困难性。

下面这3篇文章详细讲述了椭圆曲线密码算法的数学原理，不过是英文版的，但是讲述的非常详细，需要掌握的相关数学概念也讲述的很清楚。

andrea.corbellini.name/2015/05/17/…> andrea.corbellini.name/2015/05/23/…> andrea.corbellini.name/2015/05/30/…

下面这2篇是上面文章的翻译：

blog.csdn.net/mrpre/artic…> blog.csdn.net/mrpre/artic…

椭圆曲线密码算法优点

短的密钥长度，意味着小的带宽和存储要求。
所有的用户可以选择同一基域上的不同的椭圆曲线，可使所有的用户使用同样的操作完成域运算。

椭圆曲线定义

设

下图是显示了其中一种实际的椭圆曲线：

对椭圆曲线上的点，我们可以定义一种形式的加法：如果椭圆曲线上的三个点位于同一直线上，那么它们的和为

根据上面的定义导出椭圆曲线上的加法运算法则如下：当

当

下面的动画解释了为什么是切线：

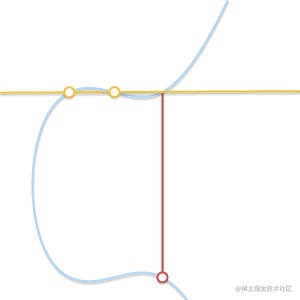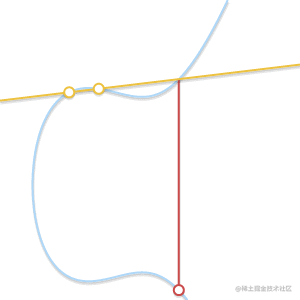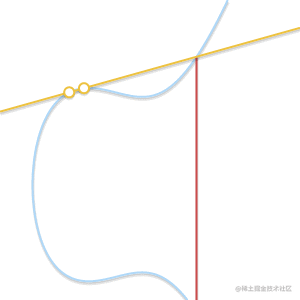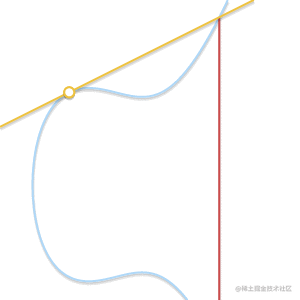
随着两个点越来越接近，过这两点的直线最终变成了曲线的切线

上面用几何的形式解释了椭圆曲线上的加法法则，下面是数学表达式。设

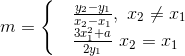
椭圆曲线上点群的离散对数问题

给定椭圆曲线上的点<img src=“https://i-blog.csdnimg.cn/blog_migrate/9189d42ac559bd3323cd7a101d6ff20c.png)和点外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传，寻找数，使得，其中称为的基于的离散对数” style=“margin: auto” />

在等式<img src=“https://i-blog.csdnimg.cn/blog_migrate/0face6da1a61cf7fd920f01e0b070340.png)中，已知外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传和点，求点比较容易，反之已知点和点，求却是相当苦难的，这个问题称为椭圆曲线上点群的离散对数问题。椭圆曲线密码体制正是利用这个困难问题设计的。在实际应用中，外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传作为私钥，而作为公钥” style=“margin: auto” />

如何计算

用这种形式表示时，计算

(取

“加倍（double)与相加（add)”算法需要这样做: • 取<img src=“https://i-blog.csdnimg.cn/blog_migrate/9189d42ac559bd3323cd7a101d6ff20c.png). • 加倍，得到外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 . • 与相加(为了得到 ). • 加倍，得到. • 与前一结果相加 (得到 ). • 加倍，得到. • 对不做任何操作. • 加倍，得到. • 与前一结果相加 (得到 ). • … 最后，我们可以计算外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传，只需7次“加倍”运算和4次“相加”运算” style=“margin: auto” />

secp256k1椭圆曲线

在比特币区块链实现中使用的椭圆曲线为secp256k1。所以这里需要学习一下。 secp256k1曲线形如
= 2^256 - 2^32 - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1](https://juejin.cn/equation?tex=p%3DFFFFFFFF%20FFFFFFFF%20FFFFFFFF%20FFFFFFFF%20FFFFFFFF%20FFFFFFFF%20FFFFFFFE%20FFFFFC2F%0A%3D%202%5E256%20-%202%5E32%20-%202%5E9%20-%202%5E8%20-%202%5E7%20-%202%5E6%20-%202%5E4%20-%201)

G的阶：

This is a graph of secp256k1’s elliptic curve <img src="https://juejin.cn/equation?tex=y%5E2%20%3D%20x%5E3%20%2B%207) over the real numbers. Note that because secp256k1 is actually defined over the field 外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传 , its graph will in reality look like random scattered points, not anything like this. 详细参考：[en.bitcoin.it/wiki/Secp25…](https://link.juejin.cn/?target=https%3A%2F%2Fen.bitcoin.it%2Fwiki%2FSecp256k1 “https://en.bitcoin.it/wiki/Secp256k1"” style=“margin: auto” />

椭圆曲线参数六元组解释：我们的椭圆曲线算法是工作在循环子群上的。几个参数含义如下：> （1）素数<img src=“https://juejin.cn/equation?tex=p)，这个值定义了有限域的大小> （2）椭圆曲线的系数、> （3）基点（子群的生成元）> （4）子群的阶> （5）协因子 (” style=“margin: auto” />

补充数学概念

这里所用到的密码学其数学基础主要是《数论》、《代数》。如果想要弄清其原理，这两部分数学基础是需要研读的。

同余式

数学上，同余（congruence modulo，符号：≡）是数论中的一种等价关系。当两个整数除以同一个正整数，若得相同余数，则二整数同余。同余是抽象代数中的同余关系的原型。

两个整数<img src="https://juejin.cn/equation?tex=a%2Cb%2C)若它们除以正整数外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传所得到的余数相等，则称对于模同余，记作。读作与关于模同余。（例）。同余式的其他详细参考：[zh.wikipedia.org/wiki/同餘](https://link.juejin.cn/?target=https%3A%2F%2Fzh.wikipedia.org%2Fwiki%2F%25E5%2590%258C%25E9%25A4%2598 “https://zh.wikipedia.org/wiki/%E5%90%8C%E9%A4%98"” style=“margin: auto” />

密码学与有限循环群

现代密码学算法和协议中，消息是作为有限空间中的数字或元素来处理的。加密和解密的各种操作必须在消息之间进行变换，以使变换服从有限消息空间内部的封闭性。然而，数的一般运算诸如加减乘除并不满足有限空间内部的封闭性。所以密码算法通常运行于具有某些保持封闭性的代数结构的空间中，这种代数结构就是有限循环群。在数学中，群是一种代数结构，由一个集合以及一个二元运算组成。群必须满足以下四个条件：封闭性，结合律，存在单位元和存在逆元。

群(Group)的定义：设

最常见的群之一是整数集

有限循环群在群的基础上满足两个额外条件：群元素个数有限以及交换律。循环群由单个元素（产生元）的叠加操作生成，最常见的有限循环群为模拟时钟。

椭圆曲线群定义

在数学上，椭圆曲线群的元素为椭圆曲线上的点，群操作为”+”,”+”的定义为，给定曲线两点<img src=“https://i-blog.csdnimg.cn/blog_migrate/9189d42ac559bd3323cd7a101d6ff20c.png)，外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传，等于和两点的连线与曲线交点沿轴的对称点，如果，则等于在曲线上的切线与曲线交点沿轴的对称点。该群的单位元为无穷远零点记作，有，点的逆元为其沿外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传轴的对称点，记作” style=“margin: auto” />

椭圆曲线有限循环群

前面介绍的椭圆曲线都是基于有理数的，但是计算机运算浮点数(小数)的速度较慢，更重要的是四舍五入浮点数会产生误差，导致多次加密解密操作后原始消息不能被还原。故考虑到加密算法的可实现性，密码学上使用基于整数的模加运算产生椭圆曲线有限循环群。基于整数的模加运算的特点：

运算速度快
精确的运算结果
产生有限循环

下面举例说明，如何产生ECC有限循环群：例如考虑

下图展示了<img src=“https://juejin.cn/equation?tex=y%5E2%3Dx%5E3-7x%2B10(mod%20%5C%2019))集合中的元素和椭圆曲线的关系。点外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传映射到点，点的对称点也由点映射到点” style=“margin: auto” />

如果取一个更大的质数

现在我们基于

如下图所示，随着

可参考：mp.weixin.qq.com/s/jOcVk7olB…

椭圆曲线的阶

椭圆曲线定义在有限域上，这也意味着，椭圆曲线上的点也是有限的。所以引出了一个问题：一个椭圆曲线到底有多少个点？定义“椭圆曲线上点的个数”为椭圆曲线的阶 (order)。至于怎么计算阶参考这篇文章吧： en.wikipedia.org/wiki/Schoof…

椭圆曲线的数乘和循环子群

在实数域，数乘（标量乘法）被定义如下：

如何计算及算法复杂度，上面有讲过，这里讲述它的一个性质。举例说明：椭圆曲线<img src=“https://juejin.cn/equation?tex=y%5E2%20%5Cequiv%20x%5E3%2B2x%2B3%20%5C%20(mod%20%5C%2097))，点外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传。现在计算的数乘” style=“margin: auto” />

上图可以化为下图的表示形式：

结果显示点<img src=“https://i-blog.csdnimg.cn/blog_migrate/9189d42ac559bd3323cd7a101d6ff20c.png)的倍数的结果只有出现5个点，其他的点从未出现；其次他们是周期出现的。显然，上面的5个点的集合，运算是封闭的。当然，不仅仅有这样的性质，其他点也有类似的性质。即，的加法构成了一个群外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传，由于属于，故是的子群。循环子群是ECC的基础” style=“margin: auto” />

子群的阶

1.首先，我们已经定义了阶就是群中点的个数。在子群中也是这样的，但是我们可以换一种表达方式：子群的阶是最小能够使得
2.子群的阶和群的阶是有关系的。拉格朗日定理说明了，子群的阶是群的阶的因子。即如果

找到子群的阶的方法（根据上面讲述的定义和性质就能得出下面的方法）：（1）计算群的阶<img src=“https://i-blog.csdnimg.cn/blog_migrate/c56dde3d825d48d684deeb8b49fa09dc.png（2）找出所有外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传的因子（3）每个的因子，然后乘以（4）在3中，找出最小的，使得满足。则是子群的阶” style=“margin: auto” />

如何找一个基点

在ECC算法种，我们希望找到一个阶数较大的子群。通常我们会选择一个椭圆曲线，然后计算它的阶

首先，拉格朗日揭示，

其次，每个椭圆曲线上的点<img src=“https://i-blog.csdnimg.cn/blog_migrate/9189d42ac559bd3323cd7a101d6ff20c.png)，外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传，因为是的阶的倍数。我们可以写成这样。假设是一个素数，我们令，则就是子群的生成元。必须是素数，若非如此，则不一定表示是的阶，因为的阶可能是外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传的一个因子。总结如下” style=“margin: auto” />

1.计算椭圆曲线的阶
2.选择一个数
3.计算
4.随机选择一个点
5.计算
auto" />
4.随机选择一个点
5.计算
6.如果接下来我将给各位同学划分一张学习计划表！

学习计划

那么问题又来了，作为萌新小白，我应该先学什么，再学什么？
既然你都问的这么直白了，我就告诉你，零基础应该从什么开始学起：

阶段一：初级网络安全工程师

接下来我将给大家安排一个为期1个月的网络安全初级计划，当你学完后，你基本可以从事一份网络安全相关的工作，比如渗透测试、Web渗透、安全服务、安全分析等岗位；其中，如果你等保模块学的好，还可以从事等保工程师。

综合薪资区间6k~15k

1、网络安全理论知识（2天）
①了解行业相关背景，前景，确定发展方向。
②学习网络安全相关法律法规。
③网络安全运营的概念。
④等保简介、等保规定、流程和规范。（非常重要）

2、渗透测试基础（1周）
①渗透测试的流程、分类、标准
②信息收集技术：主动/被动信息搜集、Nmap工具、Google Hacking
③漏洞扫描、漏洞利用、原理，利用方法、工具（MSF）、绕过IDS和反病毒侦察
④主机攻防演练：MS17-010、MS08-067、MS10-046、MS12-20等

3、操作系统基础（1周）
①Windows系统常见功能和命令
②Kali Linux系统常见功能和命令
③操作系统安全（系统入侵排查/系统加固基础）

4、计算机网络基础（1周）
①计算机网络基础、协议和架构
②网络通信原理、OSI模型、数据转发流程
③常见协议解析（HTTP、TCP/IP、ARP等）
④网络攻击技术与网络安全防御技术
⑤Web漏洞原理与防御：主动/被动攻击、DDOS攻击、CVE漏洞复现

5、数据库基础操作（2天）
①数据库基础
②SQL语言基础
③数据库安全加固

6、Web渗透（1周）
①HTML、CSS和JavaScript简介
②OWASP Top10
③Web漏洞扫描工具
④Web渗透工具：Nmap、BurpSuite、SQLMap、其他（菜刀、漏扫等）

那么，到此为止，已经耗时1个月左右。你已经成功成为了一名“脚本小子”。那么你还想接着往下探索吗？

阶段二：中级or高级网络安全工程师（看自己能力）

综合薪资区间15k~30k

7、脚本编程学习（4周）
在网络安全领域。是否具备编程能力是“脚本小子”和真正网络安全工程师的本质区别。在实际的渗透测试过程中，面对复杂多变的网络环境，当常用工具不能满足实际需求的时候，往往需要对现有工具进行扩展，或者编写符合我们要求的工具、自动化脚本，这个时候就需要具备一定的编程能力。在分秒必争的CTF竞赛中，想要高效地使用自制的脚本工具来实现各种目的，更是需要拥有编程能力。

零基础入门的同学，我建议选择脚本语言Python/PHP/Go/Java中的一种，对常用库进行编程学习
搭建开发环境和选择IDE，PHP环境推荐Wamp和XAMPP，IDE强烈推荐Sublime；

Python编程学习，学习内容包含：语法、正则、文件、网络、多线程等常用库，推荐《Python核心编程》，没必要看完

用Python编写漏洞的exp,然后写一个简单的网络爬虫

PHP基本语法学习并书写一个简单的博客系统

熟悉MVC架构，并试着学习一个PHP框架或者Python框架 (可选)

了解Bootstrap的布局或者CSS。