1. 目标
SVM是一个二类分类器,它的目标是找到一个超平面,使用两类数据离超平面越远越好,从而对新的数据分类更准确,即使分类器更加健壮。
支持向量(Support Vetor):就是离分隔超平面最近的哪些点。
寻找最大间隔:就是寻找最大化支持向量到分隔超平面的距离,在此条件下求出分隔超平面。
数据分类类别:
1)线性可分
2)线性不可分
下面首先分析线性可分的情况。
1.1 SVM特点
1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射;
2)对特征空间划分的最优超平面是SVM的目标,最大化分类边际的思想是SVM方法的核心;
3)支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量。因此,模型需要存储空间小,算法鲁棒性强;
4)无任何前提假设,不涉及概率测度;
5)SVM算法对大规模训练样本难以实施
由于SVM是借助二次规划来求解支持向量,而求解二次规划将涉及N阶矩阵的计算(N为样本的个数),当N数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对以上问题的主要改进有有J.Platt的SMO算法、T.Joachims的SVM、C.J.C.Burges等的PCGC、张学工的CSVM以及O.L.Mangasarian等的SOR算法
6)用SVM解决多分类问题存在困难
经典的支持向量机算法只给出了二类分类的算法,而在数据挖掘的实际应用中,一般要解决多类的分类问题。可以通过多个二类支持向量机的组合来解决。主要有一对多组合模式、一对一组合模式和SVM决策树;再就是通过构造多个分类器的组合来解决。主要原理是克服SVM固有的缺点,结合其他算法的优势,解决多类问题的分类精度。如:与粗集理论结合,形成一种优势互补的多类问题的组合分类器。
1.2 最优超平面求解流程
1.3 求带松驰变量的超平面流程
2. 寻找最大间隔(线性可分)
2.1 点到平面的距离
2.2 点到超平面的距离
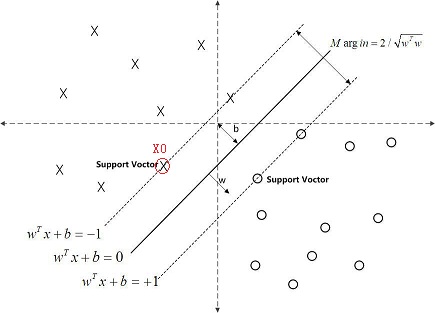
在上图中,分隔超平面为:f(x) = wTx + b=0 (注:w和x均为列向量)
点X0到分隔超平面的距离为:|wTx0 + b|/||w||
注:||w||为向量w的范数,即为w与w的内积开平方。
最大间隔为:2/||w||
2.3 使点到超平面的距离最大化
1)求最大间隔(2/||w||<为几何间隔>)的最大值:max(2/||w||) <=>
2)求||w||的最小值:min(||w||) <=>
3)因为||w||单调,为方便后面求极值时求偏导,则求
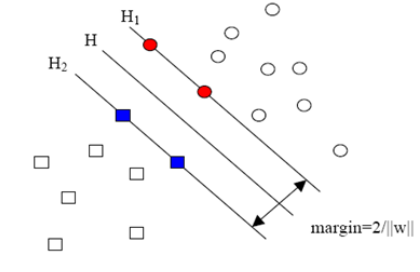
很显然||w||为0时,其值最小,反映在下图中,就是H1与H2两条直线间的距离无限大,所有样本点都进入了无法分类的灰色地带。
为了解决此问题,需要加一个约束条件:
我们把所有样本点中间隔最小的那一点的间隔定为1,也就意味着集合中的其他点间隔都不会小于1,于是有下列不等式总成立:
wTxi + b≥+1, yi=+1
wTxi + b≤-1, yi=-1 (i=1,2,…,n)
于此,此优化问题变成了求条件最优化问题:
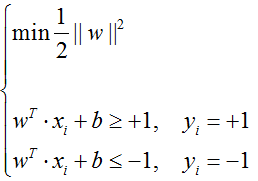
4)在求得上述最小值的情况下,从而求出w和b,即求出了分类超平面,此分类超平面可以使几何间隔最大,然后可用此分类超平面进行分类
2.4 求解极小值
2.4.1 原问题描述
1)样本集合
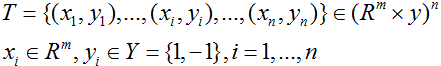
xi为:m维列向量,yi的取值为:-1或+1,样本个数为:n。
2)优化目标
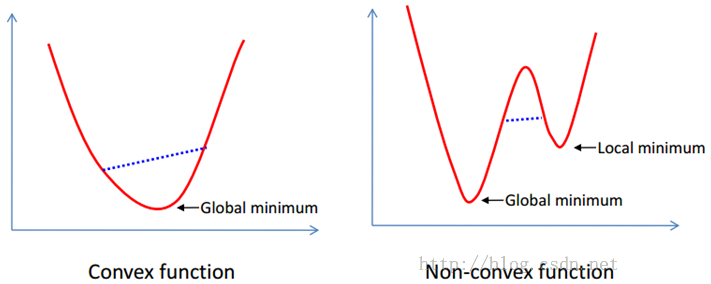
由此可见,此求最小值的是带有约束条件(s.t. subject to)的,且这是一个凸二次规划问题,所以一定会存在全局的最优解,但实际求解较为麻烦。实际的做法:将不等式约束转化为等式约束,从而将问题转化为拉格朗日求极值的问题。
为方便求最优解,需使用拉格朗日乘子把此不等式或等式约束条件融合到求最优解的函数中,从而生成拉格朗日函数。
2.4.2 生成拉格朗日函数
现在要求解如下的最小值:
上面的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (Dual Variable) 的优化问题,即通过求解与原问题等价的对偶问题(Dual Problem)得到原问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:
1)对偶问题往往更容易求解;
2)可以自然的引入核函数,进而推广到非线性分类问题。
2.4.3 什么是拉格朗日对偶性?
简单来讲,通过给每一个约束条件加上一个拉格朗日乘子(Lagrange Multiplier),定义拉格朗日函数(通过拉格朗日函数将约束条件融合到目标函数里去,从而只用一个函数表达式就能清楚的表达出我们的问题),即生成的拉格朗日函数如下所示:
然后令:
容易验证,当某个约束条件不满足时,例如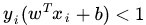
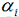
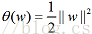
因此,在要求约束条件得到满足的情况下最小化,实际上等价于直接最小化
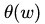
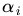
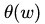
具体写出来,目标函数变成了:
这里用
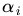
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用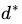
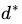

换言之,之所以从minmax的原始问题
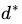
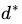

下面可以先求L 对w、b的极小,再求L 对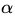
2.4.4 什么是KKT条件?
一般地,一个最优化数学模型能够表示成下列标准形式:
其中,f(x)是需要最小化的函数,h(x)是等式约束,g(x)是不等式约束,p和q分别为等式约束和不等式约束的数量。
同时,得明白以下两点:
- 凸优化的概念:
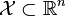 为一凸集,
为一凸集,








 1. 目标 SVM是一个二类分类器,它的目标是找到一个超平面,使用两类数据离超平面越远越好,从而对新的数据分类更准确,即使分类器更加健壮。 支持向量(Support Vetor):就是离分隔超平面最近的哪些点。 寻找最大间隔:就是寻找最大化支持向量到分隔超平面的距离,在此条件下求出分隔超平面。 数据分类类别: 1)线性可分 2...
1. 目标 SVM是一个二类分类器,它的目标是找到一个超平面,使用两类数据离超平面越远越好,从而对新的数据分类更准确,即使分类器更加健壮。 支持向量(Support Vetor):就是离分隔超平面最近的哪些点。 寻找最大间隔:就是寻找最大化支持向量到分隔超平面的距离,在此条件下求出分隔超平面。 数据分类类别: 1)线性可分 2...


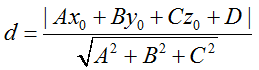
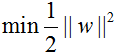
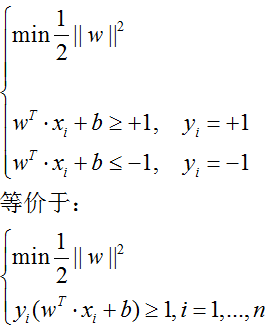
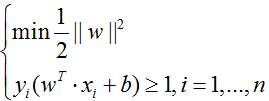
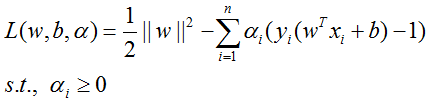
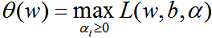
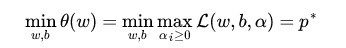
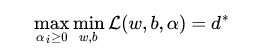
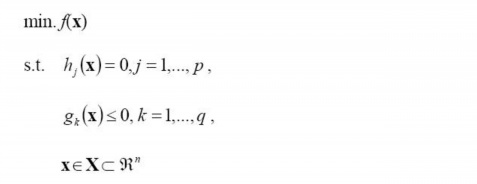
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








