【读论文10】-贝叶斯-TCN 滑坡位移预测

本文链接：https://blog.csdn.net/wangshangshang09/article/details/146934046

【读论文10】-贝叶斯-TCN 滑坡位移预测

摘要

受台风和暴雨影响，东南沿海山区经常发生滑坡灾害，其成灾机理复杂。因此，建立滑坡早期预警预测模型具有重要的理论和实践意义。

针对现有滑坡位移预测模型的不足，并结合研究区滑坡物理机制的动态演化特征，本文提出了**一种基于贝叶斯优化-时序卷积网络（Bayesian optimization-temporal convolutional networks, BO-TCN）**的新型预测模型。该模型能够对复杂的多变量时间序列数据集进行自动特征提取，在训练过程中有效避免未来数据泄漏。同时，它利用贝叶斯优化来寻找模型的最优超参数，从而提供额外的超参数调优过程解析。

与循环神经网络（RNN）相比，该模型具有更灵活的感受野、更快的训练速度和并行计算能力。

最后，本文通过分析中国福建省安溪县尧山滑坡灾害的监测数据，对比了该算法与其他常见算法的预测性能。实验结果表明，在不同预测范围内，该模型均取得了最佳的预测效果。

引言

研究背景
滑坡是一种对人类生命和财产构成威胁的自然灾害 [1, 7, 30]。可靠的预警系统可以帮助减少滑坡带来的损失，但滑坡灾害的成因机制极为复杂。滑坡演化是一个受多种因素影响的非线性动态系统 [29]，这些因素包括岩石类型、地质结构、水文地质条件和地形条件等 [16, 22, 33]。目前，仍然不清楚这些因素如何影响滑坡的演化过程。即使对滑坡机制有了清晰的理解，也很难通过精确的数学模型来描述这些机制。滑坡条件与诱发因素之间的复杂非线性关系难以用简单的代数表达式来表示 [18]。

预测模型提出（研究现状）
近年来，许多滑坡位移预测模型被提出。滑坡预测模型主要分为两类：数据驱动模型和物理模型 [4, 12]。物理模型试图通过大规模的室内模型实验以及对物理参数的现场监测来探索边坡运动规律。尽管物理模型可以为滑坡提供清晰的物理解释，但对于大型复杂滑坡的位移预测，物理模型的计算结果往往与实际监测值存在较大偏差 [5, 10, 26]。

数据驱动方法则利用数据挖掘和机器学习（ML）技术直接从收集的监测数据中推断滑坡系统行为，并据此外推滑坡位移的演化模式。由于数据驱动技术不需要滑坡系统的先验知识，并能有效补充滑坡机理研究，它们近年来已成为主流研究方向 [21, 32]。数据驱动模型包括机器学习（ML）和深度学习（DL）方法，如支持向量机（SVM）[37, 49, 51, 52]、高斯过程 [19]、随机森林（RF）[11]等，这些方法已经被用于滑坡位移预测。此外，Li 等 [17] 提出了一种新的灰色预测模型，该模型首次将双支持向量回归与Hausdorff导数算子相结合。然而，上述机器学习模型被视为静态模型，因为它们将滑坡位移预测视为静态回归问题，忽略了滑坡演化的动态特性 [43, 46]，从而限制了预测精度的提升。此外，静态模型的特征主要依赖于人工经验或特征转换方法进行提取，这一过程不仅耗时，而且需要专业的背景知识。例如，降雨强度和持续时间对滑坡位移有显著影响 [8, 9, 15]，因此需要考虑单位时间内的前期降雨量以及特定时间段内的累积前期降雨量作为预测因子。

数据驱动模型的另一个重要分支是深度学习（DL），它近年来取得了巨大进展。DL 能够自动学习数据集中的有效特征表示，并且可以长期存储关键信息，因此在预测复杂动态序列方面表现更优 [38]。近年来，人工智能方法与分解分析的结合也逐渐流行。滑坡位移的累积曲线可以被分解为趋势项和周期项，并分别对这两个分量进行预测。许多学者 [39, 41, 45, 47] 已经采用长短时记忆网络（LSTM）和门控循环单元（GRU）等循环神经网络（RNN）来预测滑坡的周期性位移。这些研究考虑了最关键的动态信息，并合理地刻画了三峡地区阶梯状滑坡的变形特征。然而，基于位移分解的当前混合预测模型在分解过程中存在“未知”数据泄露的风险 [28]。为了防止数据泄露，本文在第 4 章中讨论了相应策略。本研究的目标是尽量减少分解策略带来的潜在不确定性和复杂性。

本文采用差分方法
本文采用差分方法来稳定时间序列数据的均值，消除时间序列中的水平波动，并减少趋势性和季节性影响，从而提高数据驱动模型的预测能力 [25]。此外，Lorenzo Nava 等 [27] 评估了七种不同的深度学习技术在预测滑坡位移方面的有效性，研究涵盖了四种不同类型的滑坡（不同的地理位置、影响因素、地质环境、时间粒度和传感器测量方法），为深度学习模型的性能提供了有价值的见解。Yang 等 [42] 结合监测系统中的空间依赖性，提出了一种基于图深度学习（Graph DL）和全球导航卫星系统（GNSS）定位的多滑坡位移预测方法，以提高预测的准确性和可靠性。然而，由于循环神经网络（RNN）采用顺序训练模式，导致其训练速度较慢，尤其是在网络较深时。

相比之下，时间卷积网络（TCN）[2] 通过并行计算输出，提高了计算性能，同时避免了 RNN 常见的梯度爆炸/消失以及记忆能力不足等问题。文献综述表明，尽管大量研究已经探索了各种机器学习算法在三峡库区滑坡预测中的能力，但很少有研究将机器学习应用于不同区域的滑坡案例。然而，全球范围内有大量滑坡不位于水库区域，一些关键的缓慢滑移型滑坡对地下水位变化尤为敏感。因此，本研究提出了一种基于贝叶斯优化-时间卷积网络（BO-TCN）的新型滑坡位移预测方法，以捕捉滑坡位移多变量时间序列中的长期依赖关系，同时避免训练阶段“未知”未来数据泄露的风险。

值得注意的是，为了实现最优预测结果，需要对超参数进行精细调整。因此，我们采用高斯过程（GP）对 TCN 目标函数进行建模，并利用贝叶斯优化以并行方式高效搜索最优超参数。此外，我们利用福建省安溪县尧山滑坡的现场监测数据来确定降雨、水文条件与位移速率之间的对应关系，并使用该数据集训练和测试各预测模型，以评估所提出 BO-TCN 模型的有效性和效率。实验结果表明，该模型的预测误差最小，预测性能优于常见的时间序列预测方法。

1. 数据来源

• 监测数据：
研究使用来自中国福建省安溪县瑶山滑坡的远程无线监测系统数据。监测数据包括位移速率、孔隙水压力和降雨强度等，每小时记录一次。
• 时间范围：
数据覆盖2020年1月至6月（部分分析可能延伸至7月）。

2. 数据预处理

• 特征选择：
输入特征包括历史位移速率、孔隙水压力和降雨强度；输出为当前位移观测值。
• 时间窗口处理：
通过大小为 ( T ) 的时间窗口和滑动步长 ( S )，将时间序列数据划分为等长的子序列对（输入序列和目标序列）。

3. 划分比例

• 标准划分：
• 训练集：60%的数据（2020年1月至4月左右）。
• 验证集：20%的数据（用于超参数调优）。
• 测试集：20%的数据（2020年6月至7月，用于最终模型评估）。
• 时序依赖性：
严格按时间顺序划分，确保测试集数据在训练集之后，避免未来信息泄露。

4. 避免数据泄露的措施

• 因果约束：
模型采用时间卷积网络（TCN），确保预测时仅使用历史数据（无未来信息）。
• 滑动分解方法：
若涉及时间序列分解（如趋势项和周期项），采用滑动窗口逐段分解，避免测试集数据混入训练阶段。

5. 具体步骤（见图1框架）

数据收集：从监测系统获取多变量时间序列（图1a）。
序列分割：用时间窗口生成输入-目标子序列对（图1b）。
模型训练：TCN模型在训练集上学习（图1c）。
超参数优化：贝叶斯优化在验证集上搜索最优超参数（图1d）。
性能评估：在测试集上计算MAE、RMSE等指标（图1e）。

2 位移预测模型

所提出的 BO-TCN 模型框架如图 1 所示，该模型的开发包括四个主要步骤。首先，利用远程无线监测系统收集滑坡研究区域的数据，以获取与滑坡位移相关的因素，并筛选出模型的学习特征（图 1a）。其次，使用大小为 $T$ 的时间窗口和步长 $S$ ，将大量重叠的输入序列和目标序列构造成等长子序列对的数据集（图 1b）。然后，将拆分后的时间序列数据集输入 TCN 预测模型进行训练（图 1c）。随后，通过贝叶斯优化设置多个不同搜索策略的搜索器，以并行方式有效探索整个超参数空间，确定 TCN 的最优超参数（图 1d）。最后，使用各种评估指标来评估位移预测模型的性能（图 1e）。通过上述步骤，我们训练了一个深度神经网络（BO-TCN）用于预测滑坡位移。
在这里插入图片描述

2.1 时序卷积网络（Temporal Convolutional Networks, TCN）

Bai 等人 [2] 设计了 TCN 用于因果约束下的序列建模任务，并证明其性能优于循环神经网络（RNN）。在序列建模任务中，模型的输出是预测序列 $\hat{y}_0, \dots, \hat{y}_T$ ，对应的输入序列为 $x_0, \dots, x_T$ 。典型的因果约束要求，在预测时间 $t$ 时的输出 $\hat{y}_t$ 仅能使用此前的观测数据 $x_0, \dots, x_t$ 作为输入，而不能使用未来数据 $x_{t+1}, \dots, x_T$ 。因此，TCN 被设计为一个非线性映射函数 $f$ ：

$\hat{y}_0, \dots, \hat{y}_T = f(x_0, \dots, x_T)$

其中， $\hat{y}_t$ 仅由已知的 $x_0, \dots, x_t$ 确定，而不会受到任何未来输入 $x_{t+1}, \dots, x_T$ 的影响。为了获得能够最小化损失函数

$L(\hat{y}_0, \dots, \hat{y}_T, f(x_0, \dots, x_T))$

的最优函数 $f$ ，TCN 模型必须通过监督学习进行训练。在滑坡位移预测任务中，输入包括过去几天的历史位移、孔隙水压力和降雨强度，而输出则是当前时刻的位移观测值。

TCN 是基于传统一维（1D）卷积神经网络（CNN）的一种简单但功能强大的扩展，具有以下三个特点：

TCN 的输出序列长度与输入序列相同。
预测结果在当前时刻 $t$ 仅与历史信息相关，确保不会发生未来信息泄露。第 4 章将专门讨论滑坡预测中确保未来信息安全的重要性。
通过扩张卷积（dilated convolution）机制，TCN 的感受野和有效记忆能力随着网络深度的增加呈指数增长，从而能够捕捉更长时间跨度的历史依赖信息，提高滑坡位移的预测精度。

时序卷积网络（TCN）的特点

第一点，TCN 采用 一维全卷积网络（1D FCN） 结构 [20]，并在输入数据的两端添加相应长度的 零填充（zero-padding），确保每一层的输出与输入长度保持一致（图 2b）。此外，相较于全连接网络，采用 1D FCN 能够减少层间连接参数的数量，加快模型的收敛速度。
在这里插入图片描述

第二点，为了防止未来时间步的信息泄露，TCN 采用 因果卷积（causal convolution），它对标准卷积操作进行了调整。与传统 CNN 不同，因果卷积 强制施加时间约束，保证模型在预测时刻 $t$ 时，仅能访问当前及过去的输入，而不能利用未来信息。这种单向结构确保了时间序列的因果关系（图 2a）。

第三点，为了解决因果卷积 感受野较小 的问题，TCN 采用 膨胀因果卷积（dilated causal convolution），使感受野呈指数级增长，从而增强模型对长期依赖关系的捕捉能力。给定一维输入序列 $\in \mathbb{R}^n$ 和滤波器 $\{0,1,\dots,k-1\} \to \mathbb{R}$ ，其膨胀卷积操作 $F$ 在序列索引 $s$ 处的计算方式如下：

$*_d f)(s) = \sum_{i=0}^{k-1} f(i) x_{s - d \cdot i}$

其中， $k$ 为卷积核大小（filter size）， $d$ 为膨胀系数（dilation factor）， $_d$ 代表卷积运算， $\cdot i$ 代表回溯的历史时间步。

图 2a 展示了一个 膨胀因果卷积 的示例，其中膨胀系数 $d = 1, 2, 3, 4$ ，卷积核大小 $k = 3$ 。该结构允许在卷积过程中以 指数增长的间隔 采样输入数据，使得有效窗口大小随网络深度增加而迅速扩展。卷积核大小 $k$ 或膨胀系数 $d$ 越大，模型的感受野越宽。为了更直观地理解 膨胀因果卷积 如何提取时间序列特征，图 2c 展示了其计算机制的示例。

此外，TCN 在每一层都引入 残差模块（residual module） 进行特征提取。如图 2b 所示，残差块由 两层膨胀因果卷积 和 非线性变换 组成，在两层膨胀因果卷积后添加 ReLU 激活函数。

为了优化训练稳定性，TCN 采用以下 正则化技术：

批量归一化（Batch Normalization） [14]——用于标准化每个隐藏层的输入，以缓解梯度爆炸问题。
空间 Dropout（Spatial Dropout） [31]——在每层膨胀因果卷积后加入，以防止过拟合。

此外，由于不同层的输入和输出通道数可能不匹配，TCN 还使用 $\times 1$ 卷积 来调整残差张量的宽度，以确保张量形状保持一致。

2.2 贝叶斯优化（Bayesian Optimization）用于超参数调优

神经网络可以看作是一个黑箱函数 $f$ ，其中我们只能通过输入样本点 $x$ 获得输出 $y$ 。因此，很难直接确定存在什么样的函数关系。因此，需要设计一个可解的函数，将超参数优化问题转化为最小化未知目标函数 $f (x)$ ，并寻找最优参数 $x$ ：

$x^* = \arg \min_{x \in A} f(x)$

其中， $A$ 是需要搜索的高维超参数空间， $x$ 是最优超参数， $f (x)$ 是 TCN 模型的损失函数，这里使用均方误差（MSE）作为损失函数， $x$ 代表超参数，而不是输入数据。以 BO-TCN 模型应用于滑坡预测任务为例，超参数包括密集层中的神经元数量、滤波器、膨胀因子和批处理大小等，均由 $x$ 表示，而 $f (x)$ 则表示 TCN 模型训练集中的损失函数。当损失函数的最小值达到时，就得到了最优的超参数。

2.2.1 高斯过程回归（Gaussian Process Regression）

高斯过程（GP）是多元高斯分布的扩展，适用于无限维随机过程，其中任何有限维的组合都是高斯分布。如果高斯分布是随机变量的分布，那么高斯过程则是函数的分布，它由均值函数和协方差函数组成：

$\sim \text{GP}(m(x), k(x, x'))$

其中， $\mathbb{E}(f(x))$ 是均值函数， $\mathbb{E}[(f(x) - m(x))(f(x') - m(x'))]$ 是协方差函数。

高斯过程回归预测不会直接返回某个点 $x$ 的标量 $f (x)$ ，而是返回 $f (x)$ 在 $x$ 处可能值的正态分布的均值和方差（图 3）。

2.2.2 采集函数（Acquisition Function）

贝叶斯优化通过采集函数间接地获取 $f (x)$ 的全局最优解。采集函数在每次迭代中进行权衡，平衡高均值区域的利用（exploitation）与高波动区域的探索（exploration），以选择适当的样本点来采样超参数 [3]。常见的采集函数包括改进概率（PI）、期望改进（EI）和上置信界（UCB）。
在这里插入图片描述

在 PI 采集函数中，确定在未知点上，函数值大于 $f(x^+)$ 的概率。然后，从这些点中选择具有最高概率的点。通过使用 Z 分数归一化方法，可以比较每个未知点具有更大函数值的概率。PI 采集函数的原理如图 3 所示；最大观察值 $f(x^+)$ 位于 $x^+$ 处。 $x^+$ 区域，紫色阴影区域表示在 $x_3$ 处的改进概率 PI( $x_3$ )。相比在 $x_1$ 或 $x_3$ 采样，在 $x_3$ 处采样更可能改善 $f(x^+)$ 。PI 采集函数可以定义为：

$f(x^+) + n) = \frac{l(x) - f(x^+) + n}{r(x)}$

其中， $f(x^+)$ 是可用的最大值， $U(\cdot)$ 是标准正态分布函数， $l (x)$ 和 $r (x)$ 分别是预测值的期望和方差， $n$ 是一个超参数，它可以引导模型进行更多的探索，找到更优解。

EI 采集函数解决了 PI 采集函数只考虑改进的概率，而不考虑下一点改进的幅度的问题。EI 采集函数寻求在未知点上，函数值大于 $f(x^+)$ 的期望值：

$\left( (l(x) - f(x^+)) U \left(\frac{l(x) - f(x^+)}{r(x)}\right) \right) + r(x) \left[ 0, \max(0, l(x) - f(x^+)) \right]$

其中， $\varphi(\cdot)$ 是正态概率密度函数（PDF）。

UCB 考虑了预测值的幅度以及不确定性，GP 在观察位置的方差较小，而在未探索区域的不确定性较大。UCB 的表达式为：

$U CB (x) = l (x) + b r (x)$

其中， $b$ 是用于平衡采集函数的探索和利用能力的参数。

贝叶斯优化基础上的 TCN 超参数搜索算法过程如下（图 2(d)）：

初始化代理模型的先验分布（图 1d 中的蓝色区域）。
通过优化采集函数找到点 $x_{n+1} = \arg \max_{x \in A} u(x | D_{1:n})$ （图 1d 中的橙色曲线）。
训练 TCN 模型，计算验证集的损失函数值 $y_{n+1} = f(x_{n+1})$ （图 1d 中的红点），并更新当前的最佳值。
将结果添加到先前的样本中 $D_{1:n} = D_{1:n} \cup \{x_{n+1}, y_{n+1}\}$ ，并使用 GP 更新代理模型，得到后验分布（作为下一步的先验分布）。
重复步骤（2）–（4），直到达到最大迭代次数。

2.3 模型性能评估方法

为了评估本文提出的滑坡位移预测模型的性能，我们将模型预测值与实际值进行比较，以评估预测的准确性。我们使用了平均绝对误差（MAE）、均方根误差（RMSE）和决定系数（ $R^2$ ）来评估预测准确性，具体定义如下：

平均绝对误差（MAE）:

$\frac{1}{N} \sum_{t=1}^{N} | \hat{y}_t - y_t |$

均方根误差（RMSE）:

$\sqrt{\frac{1}{N} \sum_{t=1}^{N} (\hat{y}_t - y_t)^2}$

决定系数（ $R^2$ ）:

$R^2 = 1 - \frac{\sum_{t=1}^{N} (\hat{y}_t - y_t)^2}{\sum_{t=1}^{N} (y_t - \bar{y})^2}$

其中， $\hat{y}_t$ 是时间 $t$ 的预测值， $y_t$ 是时间 $t$ 的实际值， $\bar{y}$ 是所有实际值的算术平均值， $N$ 是样本数量。

3 Yaoshan滑坡的位移预测

3.1 地质条件

该大规模活跃滑坡（25.0209°N, 117.9592°E）是典型的慢速滑坡，位于中国福建省安溪县西坪镇南约8公里的姚山村（见图4 P1）。该滑坡长500米，宽200米，平均厚度13米，主要滑动方向为东北15°。滑坡地带属于中低山地形，具有构造侵蚀特征，海拔350至470米，位于坡面中部的坡脚（见图4 P2）。该坡面整体地形特征表现为上部陡峭、下部较缓，坡背的集水区达80万平方米，极为有利于地表水和地下水的补给，进一步促进滑坡变形带的水文变化。
在这里插入图片描述

在地形方面，滑坡呈现出纵向凹陷的形态，从后缘至前缘；横向呈现出从东到西的驼峰形态，山谷的切割深度和宽度不一。滑坡的纵向印象从后缘至前缘呈舌形。坡面上有三个主要的沟谷，其中东西两侧的沟谷较深，宽约10米，深约5米，中间的沟谷相对较浅。这三条沟谷长期有水流，流量约为150-300立方米/天。坡面的梯田种植有茶叶、蔬菜、竹子和稻米等经济作物，植被覆盖率为70%-80%。

根据该研究区域的地质调查，晚侏罗世的凝灰岩和凝灰岩熔岩层（J3nc）暴露出地表，并且在距离该站点北侧约800米处，存在一个30°NE方向、60-70°倾角的正断层，该断层沿断裂带侵入花岗岩脉。该断层自北向南延伸，通过该站点。由于该区域地表大部分被滑坡堆积物覆盖，且未见明显的岩床露头，表面断层迹象不明显；然而，在地表调查和深钻孔曝光中，断层迹象较为明显。如图5所示，该滑坡的下土层由不同程度风化的凝灰岩（基岩）组成，表面覆盖有冲积砾石土和残余粘土。

3.2 倾斜仪数据

滑坡的滑动面位置是通过倾斜仪测量获得的。倾斜仪孔位（CX1-CX6）的布置如图4 P2所示。2019年3月至2019年7月期间使用倾斜仪记录的深层水平位移数据如图6所示。倾斜仪数据表明，滑坡具有多阶段的滑动面。坡面上下区域（CX3和CX4）的滑动面位于冲积砾石土与残余粘土之间的交界面，而坡中部的滑动面则为残余粘土与凝灰岩之间的接触面。滑动带的深度为12-16米，厚度为1-1.5米。
在这里插入图片描述

3.3 位移率、孔隙水压力和降雨分析

为了更好地研究姚山滑坡的运动机制，设计了一个远程无线监测系统（见图1a）。在滑坡现场中轴位置的中部（S1）和下部（S2）分别安装了雨量计、孔隙水压力计、倾斜仪和水位计，用于实时长期监测。每个传感器的数据每小时记录一次，并实时传输至监测系统。图7a展示了2020年1月至6月期间姚山滑坡监测站S1的监测数据，从中可以得出以下观察结果：
在这里插入图片描述

姚山滑坡主要沿连续的剪切带发生摩擦滑动。随着地下水位波动，滑坡经历了间歇性和交替的静止与加速运动。滑坡位移的不同阶段具有明显的台阶型增长特征。此外，滑坡速度与孔隙水压力变化之间有很强的相关性（见图7c），这表明滑坡速度、孔隙水压力与降雨反应之间的联系。滑坡运动在孔隙水压力急剧增加时加速，随着孔隙水压力的消散而减速。然而，滑坡位移的减速速度明显快于孔隙水压力的减速速度。
姚山滑坡跳跃期的特征是：滑坡位移在短时间内达到峰值，随后过渡到长期的蠕变阶段。这一行为主要由大气降水渗透进入滑坡的残积砾土和砂砾土中引起孔隙水压力的快速上升，从而减少滑动带的剪切强度并触发滑坡。此外，滑坡的相对缓坡使得在滑坡发生后孔隙水压力能够迅速消散，减少坡体的惯性力，滑动带的粘性阻力在此过程中起到了制约作用。
滑坡位移变化不仅仅取决于孔隙水压力的大小。无论是干季还是雨季，滑坡位移只有在持续降水或暴雨条件下孔隙水压力发生较大波动时才会发生。当降雨停止且孔隙水压力尚未恢复到降雨前的水平时，坡面逐渐恢复稳定。这是因为研究区滑坡的上层由冲积砾土组成，该层土壤容易通过大气降水的渗透进行补充，而相邻的残余粘土层作为相对不透水层，导致两种土层交界处积水，从而形成滞水水位和坡面渗水场。在长期渗水过程中，优先流动通道容易形成，逐渐侵蚀滑坡的冲积砾土，从而形成地下水管道网络渗透系统。由于此机制，滑坡脚部常自然出现泉水（见图7c）。在降雨过程中，如果土壤管道网络中的水浓度超过管道流量转移能力，土壤管道的空腔容易被水填满，增加了周围基质的孔隙水压力[24, 34]。冲积砾土中的内部优先流动、俯冲与拖力耦合作用机制导致了坡体的不稳定。

因此，本研究区滑坡的运动机制非常复杂，受到多个因素相互作用的影响。滑坡位移数据表现出显著的非平稳性和非线性特征，这使得位移预测更加具有挑战性。

3.4 预测结果与分析

3.4.1 贝叶斯优化的超参数搜索

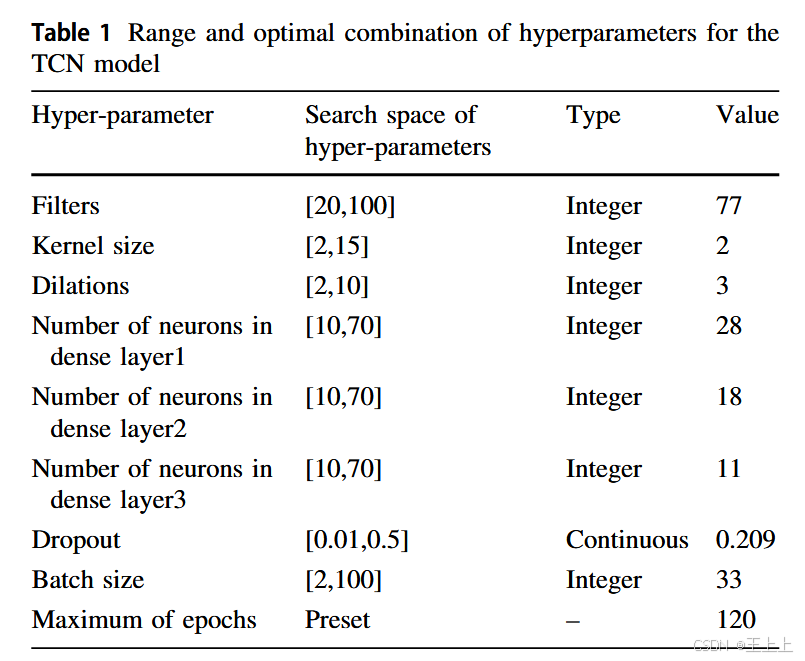
在模型开始学习之前，必须设置超参数，而不是使用通过训练获得的参数。超参数的选择对于神经网络的成功至关重要，因为它们会严重影响学习模型的表现。例如，如果学习率设置得过高，模型容易通过偶然的巧合找到模式；而如果学习率设置得过低，模型则可能错过数据中的重要模式。此外，理解不同数据集和模型可能具有不同的超参数也非常重要。因此，必须选择一组理想的超参数，使得学习模型的表现和效能最大化。本文通过贝叶斯优化调整了TCN架构的超参数（批量大小、丢弃率、核大小、神经元数量、过滤器和扩张）。超参数搜索范围和最佳超参数组合见表1；输入层和输出层的神经元数分别为3和1；学习率通过早期终止函数动态调整，训练过程中最大迭代次数为120次。图8展示了贝叶斯优化在验证数据集中的搜索损失趋势；第23次迭代时达到了全局最优，损失最小（红色填充区域）。图9显示了TCN模型的最优超参数组合；最优的超参数组合为：过滤器=77，密集层1=28，密集层2=18，密集层3=11，扩张=3，批量大小=33，丢弃率=0.209，核大小=2，这是最小化搜索损失并达到全局最优的超参数组合。
在这里插入图片描述

3.4.2 预测结果

本研究的目的是利用孔隙水压力、降雨量和历史位移率等因素预测研究区的滑坡位移率。我们应用了所提出的BO-TCN模型框架来对姚山滑坡2020年1月至7月的短期数据集进行评估，测试了该模型在实时预测中的表现。数据集分为三部分：60%作为训练数据集，20%作为验证数据集，20%作为测试数据集（见图7a）。首先，我们将BO-TCN模型与静态模型（BO-RF和BO-SVM）进行比较，并突出了其在处理滑坡演化动态预测中的优势（见图10a）。此外，BO-TCN模型的表现与传统深度学习模型（如1D-CNN、LSTM和GRU）相比，可以达到相似甚至更优的结果（见图10b），在滑坡预测任务中展现出优越性。我们使用四个广泛使用的指标（公式（8）-（10））评估了滑坡位移预测模型的定量表现。图11和表2进一步展示了各种滑坡预测模型在测试数据集上的实时预测表现。比较实验的参数设置见表3。BO-SVM和BO-RF仍为静态模型，在单一时间点学习输入输出规则。虽然它们能够捕捉训练数据集中的趋势，但在预测测试数据集中的局部峰值时存在困难。相比之下，动态深度学习模型（BO-TCN、BO-CNN、BO-LSTM和BO-GRU）保持过去信息在其隐藏状态中，从而传递上下文信息，动态地探索监测点的时间特性。它们能够有效地捕捉序列中的峰值变化，特别是在位移率发生急剧变化时。因此，它们在准确性和稳定性方面明显优于静态模型。与BO-LSTM和BO-GRU模型相比，提出的BO-TCN模型通过堆叠卷积层并增加卷积核的感受野，展现了稳定的梯度。该设计缓解了梯度爆炸/消失的问题，具有更强的泛化能力。此外，它的预测结果表现出最小的滞后，这对于滑坡预警系统（EWS）至关重要。BO-TCN实现了最小的预测误差（MAE=0.3114，MSE=0.1841，MSE=0.4291，R²=0.9615），这与图10中的视觉/定性分析一致，验证了BO-TCN在实际应用中的有效性和优越性。
在这里插入图片描述

3.4.3 预测误差分析

在本小节中，我们进一步分析了预测误差。图12展示了BO-TCN模型和其他基准模型在不同时间点的堆叠预测误差，可以观察到每个模型的偏差。基于BO-TCN的混合模型产生的误差较小，因为在滑坡位移剧烈变化时，预测误差显著较低。各种模型的误差分布如图13所示，结果表明BO-TCN的误差更集中在零附近，且变化不大。此外，误差的概率密度函数（PDF）符合正态分布（见图14）。BO-TCN的高准确性和鲁棒性得到了证实，混合模型的峰度高于其他三种基准模型。

在这里插入图片描述

4 讨论

4.1 BO-TCN滑坡位移预测模型对预警系统（EWS）的贡献

滑坡预测是早期预警系统（EWS）的关键组成部分，对于滑坡的预防和减灾具有至关重要的意义 [13, 23]。然而，一些现有的滑坡EWS依赖于特定滑坡及其影响因素之间的历史交互关系。预测慢速滑坡最常用的方法是基于临界降雨阈值 [6, 40]。这种方法因其应用简便和易于解释而广泛使用，成为发布紧急预警的常见手段。然而，尽管这一方法可以提供可靠的预警，它常常忽视或不准确地估算预期滑坡位移的大小以及最大位移的时间。相比之下，BO-TCN模型能够提前准确地预测滑坡变形速率的峰值时刻和加速度。这些预测结果可以作为发布预警的阈值值 [50]。

然而，降雨阈值方法仅将预期降雨作为唯一的触发变量，而BO-TCN模型则不考虑未来的协变量，其工作原理假设当前和过去的触发因素会影响未来滑坡的行为。因此，为了充分发挥这两种方法的潜力，建议将两者结合起来。在这一集成框架中，降雨阈值方法根据未来的降雨预报数据发布预警，而BO-TCN模型则基于当前和过去的数据预测加速度的大小。此外，深度学习（DL）和其他基于数据驱动的预测模型依赖于历史监测数据作为模型训练的基础。长时间序列的监测数据可以更有效地捕捉其总体变异性和综合行为范围。DL具有保留关键信息的能力，随着监测数据量的增加，性能得到了增强。然而，本研究由于监测数据的稀缺遇到了限制。现场条件导致部分滑坡传感器的数据缺失或噪声，导致用于训练和测试的连续数据有限。因此，长期高质量监测数据的可用性对于有效的预警应用具有重要意义。

4.2 基于分解的混合模型的挑战

尽管大多数滑坡位移预测模型是基于位移分解的混合预测模型 [36, 41, 44, 47, 48]，但它们在位移分解过程中涉及了未来的“未知”数据 [28]。在滑坡位移时间序列数据的情况下，基于位移分解的模型首先将整个数据集分解为趋势项和周期项的位移子序列。每个子序列进一步划分为训练和测试数据集，用于分别构建和评估预测模型。通过这种方式，未来的“未知”数据（本应被预测的部分）被引入到训练阶段 [35]。实际上，如果时间t是当前时间点，那么要分解的时间序列只能包括到t为止的数据，因为之后的数据是未知的。因此，在开发基于位移分解的滑坡位移预测模型时，模型的训练阶段不涉及“未来”数据。这样，在开发基于位移分解的滑坡预测模型时，未来数据不会被用于训练阶段。

假设用于训练和测试滑坡位移预测模型的时间序列数据记为 D，总长度为 T + k 数据点。前T个数据点用于模型训练，接下来的k个数据点用于模型测试。目标是利用前L个数据点预测接下来的M个数据点。为了避免涉及“未来”数据，可以采用以下两种解决方案：

多次训练与多次预测

1. 将时间序列D1:T分解，获得表示趋势和周期分量的位移子序列。为每个子序列构建并训练预测模型。
1. 模型训练完成后，使用数据 DT(L-1):T 获取每个子序列模型的M个预测输出。将这些输出合并，以获得DT+1:T+M的预测。
1. 将时间序列D1+M:L+M分解，并重复步骤（1）和（2）。继续此过程直到获得DT+1:T+k的预测。
1. 使用DT+k的预测值与对应的真实值计算评估指标。

通过滑动分解过程构建样本

(1) 分解时间序列
将时间序列 ( D_{1:L} ) 分解成子序列集，记为 ( X_{i1} ) (长度为 ( L ))，然后进一步将 ( D_{M+1:L+M} ) 分解成子序列集，记为 ( Y_{i2} ) (长度为 ( L ))。接着，对于每个子序列，构建样本对 ( (x_{i1}, y_{i2}) )，如图 15 所示。

(2) 滑动窗口生成样本
通过上述方法，每次滑动窗口 ( M ) 个数据点，直到训练集完全消耗为止，生成所有的训练样本。

(3) 训练预测模型
利用前两步得到的数据，训练用于预测这两个位移子序列的模型。

(4) 正式预测
在正式预测时，每次迭代选择最近的 ( L ) 个数据点进行分解，并进行重叠预测。

上述方法要求对时间序列数据进行逐步分解，这需要大量的计算资源。此外，在方法1中，每个预测模型需要反复构建和训练，这进一步增加了计算资源的需求。尤其是在需要高分辨率的滑坡预测时，这可能会成为一个挑战。因此，优化计算资源的使用，可能是提升此方法在实际应用中可行性的关键。

5. 结论

滑坡预测在灾害减缓中发挥着至关重要的作用，是一种成本效益高的减灾策略。然而，由于滑坡的间歇性和复杂性，准确预测滑坡位移序列仍然是一个挑战，对于可靠的预警系统至关重要。本研究提出了一种新型的位移预测模型BO-TCN，基于2020年1月至6月期间从安溪县姚山滑坡灾害中获得的监测数据，旨在提供更加准确和稳健的滑坡位移预测。与其他基准模型的对比分析得出以下结论：

姚山滑坡的运动行为
姚山滑坡表现为间歇性运动，主要受降水事件的影响，并表现出典型的阶梯形变行为。由于坡面上冲积土层中已发育完善的管道网络渗透系统，滑坡位移不仅仅依赖于孔隙水压力的绝对值。滑坡的变形是由优先流、潜没和拖力等耦合机制共同作用的结果。
BO-TCN模型的有效性
BO-TCN模型有效避免了在训练阶段使用未来数据的泄漏问题，这是当前基于位移的滑坡预测模型的常见问题。预测结果表明，BO-TCN模型达到了最低的预测误差（MAE、MSE、RMSE和R2），证明了该模型在滑坡位移预测研究中的高实用性和广泛适用性。
BO-TCN模型优于其他模型
比较结果确认，动态深度学习模型（如BO-TCN）在滑坡演变的动态预测中明显优于静态模型（如BO-SVM和BO-RF）。此外，BO-TCN模型在滑坡预测任务中也优于传统的深度学习模型（如1D-CNN和RNN（LSTM和GRU））。BO-TCN模型展现出更强的泛化能力，能够准确预测姚山滑坡的阶梯形变，且预测结果稳定、精准。
计算效率
提出的BO-TCN模型具有较高的计算效率和可接受的计算复杂度，特别是在并行和分布式计算环境下应用时，具有明显优势。这对于大数据时代尤为重要，能够高效处理大规模数据集。此外，BO-TCN模型适用于其他具有非平稳性和非线性特征的时间序列预测任务。

综上所述，BO-TCN模型在滑坡预测方面取得了显著进展，能够提供精准及时的预测，有助于滑坡灾害的预防和预警。该模型的有效性和计算效率确保了其在滑坡研究以及其他时间序列预测应用中的广泛适用性。

参考文献
[1] Yang J, Huang Z, Jian W, et al. Landslide displacement prediction by using bayesian optimization–temporal convolutional networks[J]. Acta Geotechnica, 2024, 19(7): 4947-4965.