正则表达式-->NFA--->DFA--->最简DFA
DFA(有限自动机,每个状态的下一步都是确定的,没有空。只有一个开始状态,只有一个结束状态)
NFA(有可能转到多个状态,可能有空)
※由正则表达式转到NFA:
基本可以分成3种:
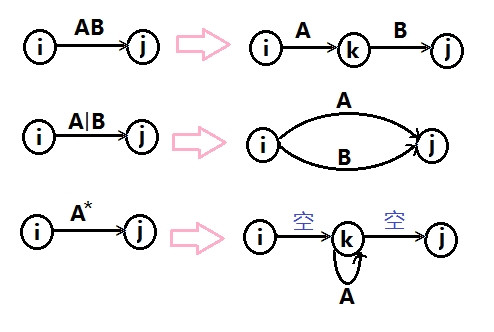
AB(连接)
A|B(或)
A*(0到多个A)
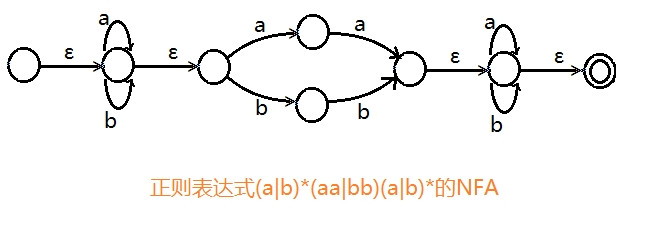
例:正则表达式(a|b)*(aa|bb)(a|b)*的NFA
NFA和DFA匹配串的时间空间复杂度

※NFA的确定化:NFA转DFA
空闭包,子集法
原理:有些状态是在做同样的工作,他们的工作完全可以用一个状态来做,把这些相同功能的状态组合成一个集合,并把它重新命名为一个状态。
例:
将以下NFA转换为DFA
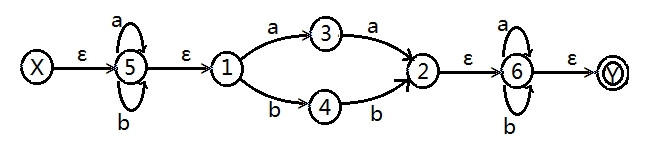
按下表不断构建,直到Ia,Ib中出现的集合,全部都出现在I中。并且将他们重新编号
(终态是那些有Y的集合,Y为原先NFA的终态)
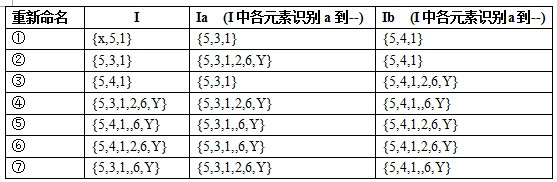
转成DFA的结果:
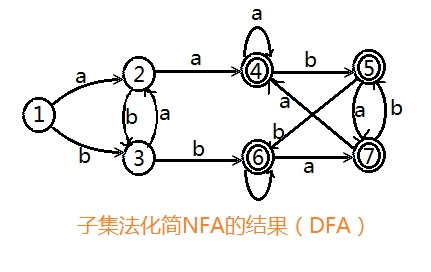
※DFA化简成最简DFA:
1.划分终态,非终态: P={{4,5,6,7},{1,2,3}}
2.{4,5,6,7}内部能识别a和b,不再划分,(成一个大的部门处理相同的事情)
3.{1,2,3} 根据识别a的能力,划分为{1,3}和{2}(1,3识别a都转到3)
根据识别b的能力,划分为{1} {3} {2}
4.(此例不用考虑这条)删除死循环(即一个对所有输入符号都有到自身转换的非终态)和不可达状态
结果P={{4,5,6,7},{1},{2},{3}}
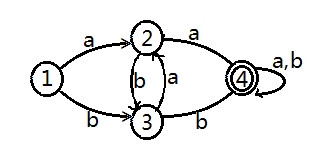
给四个划分再重新命名 变成1,2,3,4
结果是:






















 8715
8715

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








