C++ 两点之间的距离

C++ 两点之间的距离

现在我们已知点S₁和点S₂的位置 (这里x和y反过来写，方便数组储存) ，要求两点之间的距离。

勾股定理求解

使用勾股定理求解：
$$a^2+b^2=c^2$$
a和b表示三角形的两条直角边，c表示三角形的斜边，而这里的斜边就是我们要求的距离。

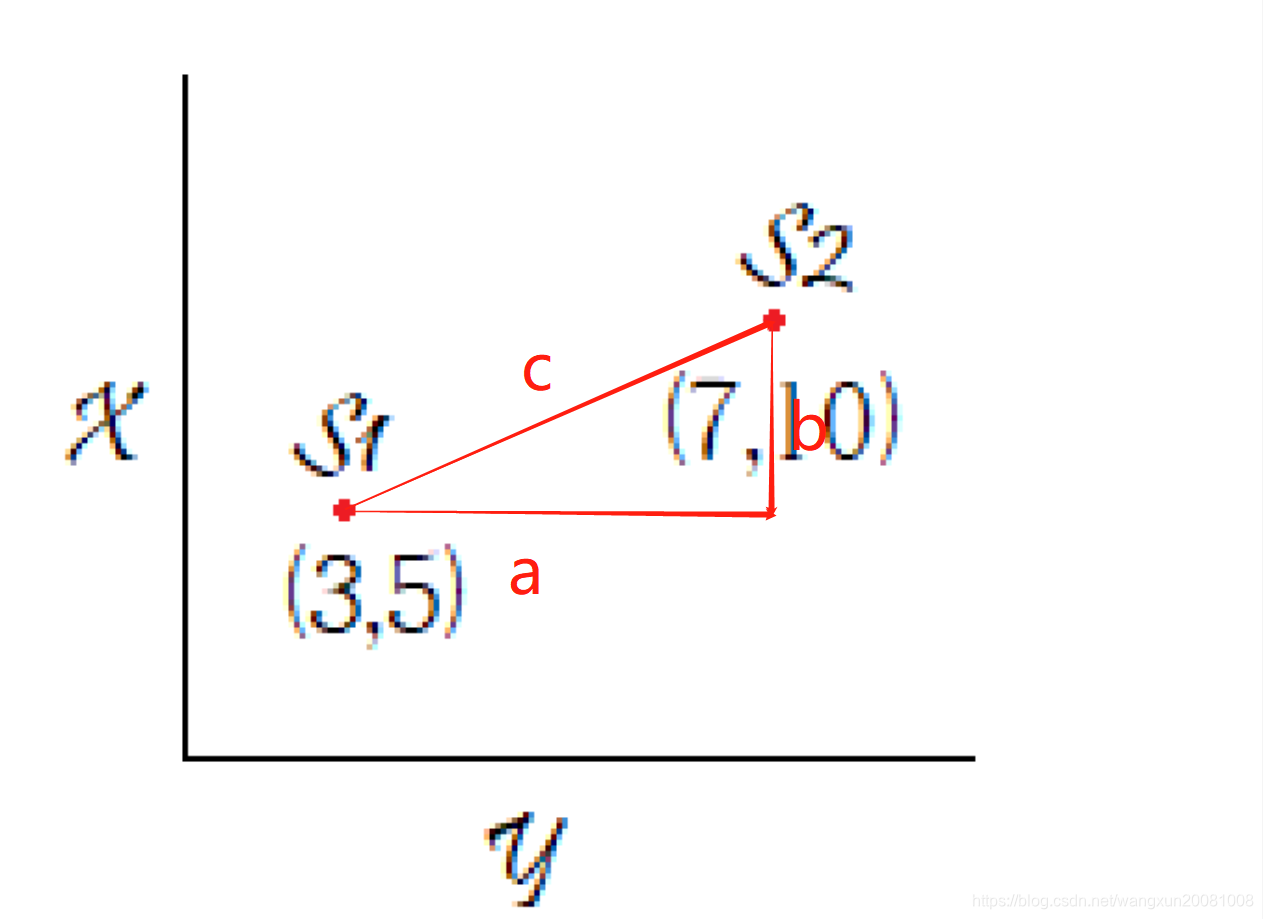
现在我们要求出a和b的长度:
$$a=|s1.x-s2.x|，b=|s1.y-s2.y|$$
$$a=4，b=5$$
这里我们用了绝对值，防止出现负数。接下来再求出c:
$$a^2+b^b=c^2，c=\sqrt{a+b}$$
$$c=\sqrt{4^2+5^2}$$
$$c=\sqrt{41}$$
大功告成，接下来就贴上代码：

#include <bits/stdc++.h>
using namespace std;

int s1x,s1y,s2x,s2y;
double a,b,c;

int main() {
	cin>>s1x>>s1y>>s2x>>s2y;
	a=abs(s1x-s2x);
	b=abs(s1y-s2y);
	c=sqrt(a*a+b*b);
	cout<<"dis = "<<c<<endl;
	return 0;
}