FFT:
这里使用基二FFT算法,非基二FFT难度有点大,等以后补充。
对于非2的幂次方长度的序列,我们采用的是补零法:即:我们的FFT只能用于分析或者产生频谱,而不能求得某一特定点的DFT。
首先定义复数操作,实际上,复数操作的定义非常繁琐,这里我只定义了在本次应用中能用到的操作:
const double PI=3.1415926;
const double prec=0.00001;//控制精度
const char MARK='j';//复数的标志符,工程上喜欢使用j,数学上喜欢使用i
//下面是复数结构,主要定义了加减乘除操作符
template<typename T>
class complex
{
public:
T real;
T imag;
public:
complex(T a=T(),T b=T()):real(a),imag(b){ }
//copy和copy assigment,析构函数可以使用编译器合成的
public:
inline complex conjugate()const;
inline T module() const;
public:
inline complex& operator/=(int rhs);
};
template<typename T>
complex<T> operator+(const complex<T>& lhs,const complex<T>& rhs)
{
return complex<T>(lhs.real+rhs.real,lhs.imag+rhs.imag);
}
template<typename T>
complex<T> operator+(const int& lhs,const complex<T>& rhs)
{
return complex<T>(lhs+rhs.real,rhs.imag);
}
template<typename T>
complex<T> operator+(const complex<T>& lhs,const int& rhs)
{
return complex<T>(lhs.real+rhs,lhs.imag);
}
template<typename T>
complex<T> operator+(const double& lhs,const complex<T>& rhs)
{
return complex<T>(lhs+rhs.real,rhs.imag);
}
template<typename T>
complex<T> operator+(const complex<T>& lhs,const double& rhs)
{
return complex<T>(lhs.real+rhs,lhs.imag);
}
template<typename T>
complex<T> operator+(const T& lhs,const complex<T>& rhs)
{
return complex<T>(lhs+rhs.real,rhs.imag);
}
template<typename T>
complex<T> operator+(const complex<T>& lhs,const T& rhs)
{
return complex<T>(lhs.real+rhs,lhs.imag);
}
//---------------------------------------------------------------------------
template<typename T>
complex<T> operator-(const complex<T>& lhs,const complex<T>& rhs)
{
return complex<T>(lhs.real-rhs.real,lhs.imag-rhs.imag);
}
template<typename T>
complex<T> operator-(const int& lhs,const complex<T>& rhs)
{
return complex<T>(lhs-rhs.real,-rhs.imag);
}
template<typename T>
complex<T> operator-(const complex<T>& lhs,const int& rhs)
{
return complex<T>(lhs.real-rhs,lhs.imag);
}
template<typename T>
complex<T> operator-(const double& lhs,const complex<T>& rhs)
{
return complex<T>(lhs-rhs.real,-rhs.imag);
}
template<typename T>
complex<T> operator-(const complex<T>& lhs,const double& rhs)
{
return complex<T>(lhs.real-rhs,lhs.imag);
}
templat







 本文介绍基二快速傅里叶变换(FFT)算法,适用于2的幂次方长度的序列。通过补零法处理非2的幂次方长度序列,主要关注FFT在频谱分析中的应用。文中定义了复数操作,并给出了迭代器版的FFT实现。
本文介绍基二快速傅里叶变换(FFT)算法,适用于2的幂次方长度的序列。通过补零法处理非2的幂次方长度序列,主要关注FFT在频谱分析中的应用。文中定义了复数操作,并给出了迭代器版的FFT实现。
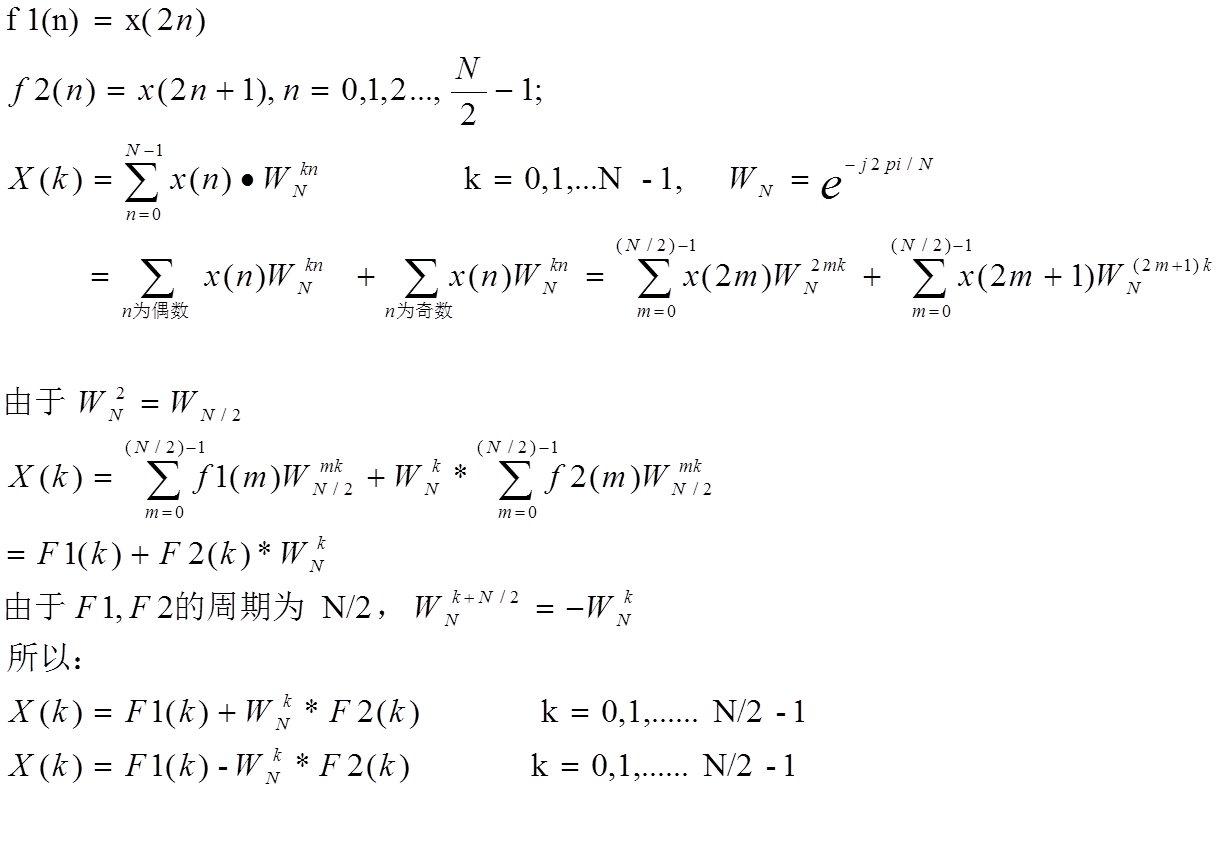
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5103
5103

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








