目录
4.1基本概念
4.1.1复数
复数C的定义如下:
C=R+jl
共轭复数C*定义如下:
C*=R-jI
有时,在极坐标下表示复数很有用:
C=|C|(cosθ+jsinθ)
其中,是复平面的原点到点(R,I)的向量的长度,θ是该向量与实轴的夹角。
4.1.2傅里叶计数
具有周期T的连续变量t的周期函数ft)可以被描述为乘以适当系数的正弦和余弦和。我们知道,这个和就是傅里叶级数,它具有如下形式:
;
其中,,n=0,-+1,-+2.......
4.1.3冲激及其取样特征
线性系统和傅里叶变换研究的核心是冲激及其取样特性。连续变量t在t=0处的单位冲激表示为δ(t),其定义是:
假设f(t)在t=0处是连续的,取样特性的一种更为一般的说明涉及位于任意点t。的冲激,表示为δ(t-to)。在这种情况下,取样特性变为:
图4.3显示了一个冲激串。冲激可以是连续的或离散的。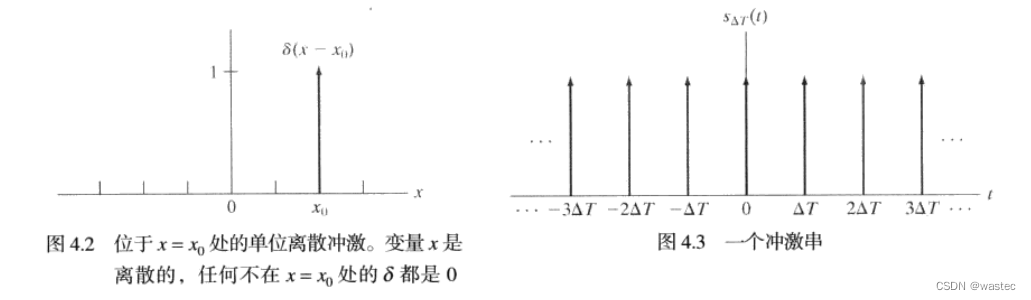
4.1.4连续变量函数的傅里叶变换
由{f(t)}表示的连续变量t的连续函数f(t)的傅里叶变换由下式定义:
t可以表示任何连续变量,频率变量μ的单位取决于t的单位。例如,如果t表示单位为秒的时间,则μ的单位为周/秒,或者赫兹(Hz)。如果t表示的是以米为单位的距离,则μ的单位是周/米,等等。换句话说,频率域的单位是独立于输入变量的每单位周期的。
4.2.5卷积
卷积定义如下:
其中,负号表示刚刚提及的翻转,t是一个函数滑过另一个函数的位移,而是积分假变量。现在我们假定函数从-无穷扩展到+无穷。
4.2取样和取样函数的傅里叶变换
4.2.1取样
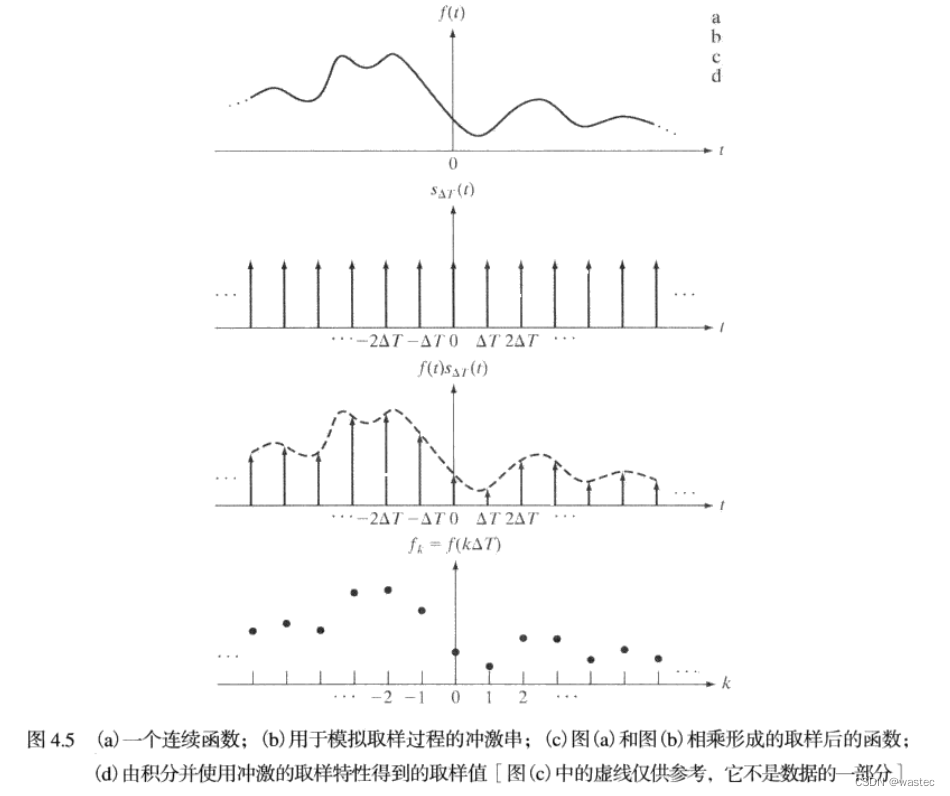
参考图4.5,考虑一个连续函数f(t),我们希望以独立变量t的均匀间隔(△T)取样。我们假定函数对于t从-无穷到+无穷扩展。模拟取样的一种方法是用一个△T单位间隔的冲激串作为取样函数去乘以f(t),即:
如图4.5(c)所示。每个取样值由加权后的冲激“强度”给出,我们可通过积分得到它。也就是,序列中的任意样式值由下式给出:
其中,我们利用了式(4.2-10)中δ的取样特性。式(4.3-2)对任何整数k=…,-2,-1,0,1,2,…都成立。图4.5(d)显示了结果,它由原始函数的等间隔取样组成。
4.2.2取样函数的傅里叶变换
取样函数的傅里叶变换
是
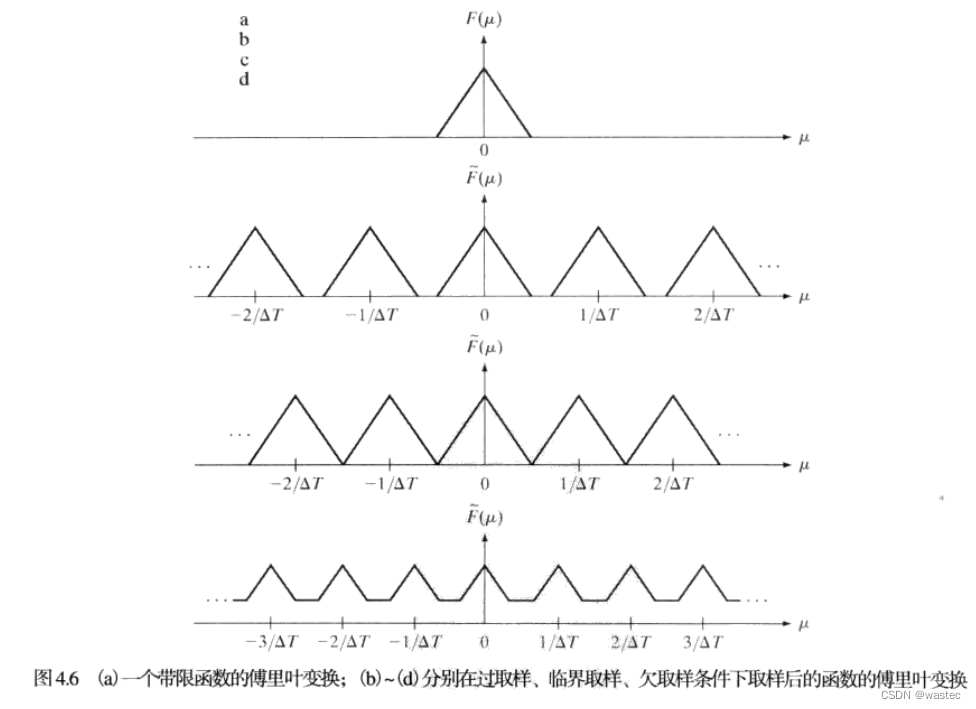
图4.6是前面结果的一个图示总结。图4.6(a)是函数f(t)的傅里叶变换F(μ)的简图,图4.6(b)显示了取样后的函数的变换F(μ)。在图4.6(c)中,取样率刚好足以保持F(μ),但在图4.6(d)中,取样率低于保持不同F(μ)拷贝的最小取样率要求,这样,就不能保持原始变换。
4.2.3取样定理
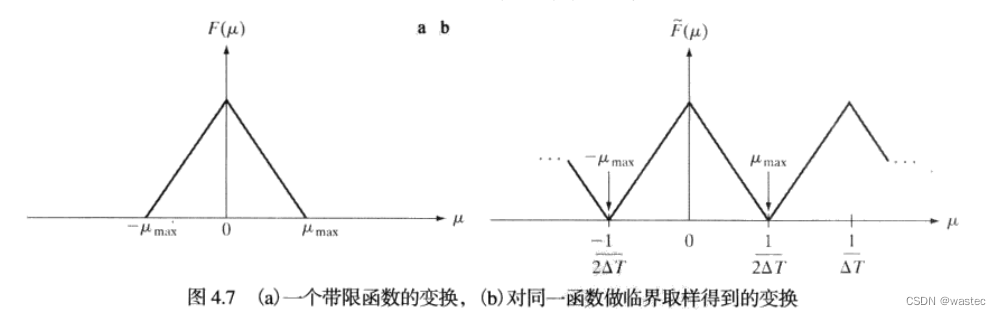
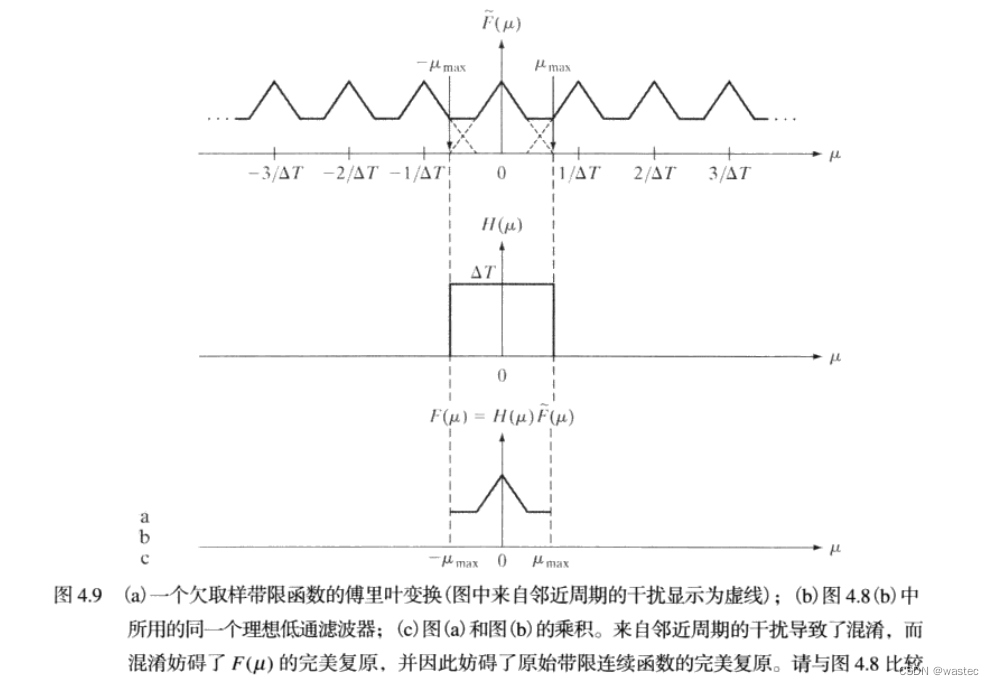
对于以原点为中心的有限区间(带宽)[-μmax,μmax]之外的频率值,其傅里叶变换为零的函数f(t)称为带限函数。图4.7(a)就是这样一个函数,它是图4.6(a)的一个放大部分。类似地,图4.7(b)是
图4.6(c)所示临界取样后的函数的傅里叶变换更详细的视图。较低的1/△T值将导致F(μ)中的周期融合,较高的1/△T值在周期之间会提供更为清晰的间隔。
4.2.4混淆
使用图4.9(b)中的理想低通滤波器,将会得到如图4.9(c)所示的一个变换,该变换已被来自邻近周期的频率破坏了。然后,反变换会产生t的一个破坏了的函数。由函数欠取样导致的这种效果就是周知的频率混淆,或简称为混淆。在字面上,混淆是一个过程,在这一过程中,一个连续函数的高频分量在取样后的函数中用低频“化妆”了。
4.2.5取样后的数据重建函数
我们将简单地用显示介质显示一幅图像的行为都要求来自其样本的图像重建。可导出f(t)的如下空间域表达式:
4.3单变量的离散傅里叶变换(DFT)
4.3.1由取样后的函数连续变换得到DFT
一个取样过的、带限的、扩展到-无穷到+无穷范围的函数的傅里叶变换,也是扩展到-无穷到+无穷。范围的连续的周期函数。实践中,我们处理有限数量的样本,因此本节的目的是推导对应于这种样本集合的DFT。总结前文可以得到:
,m=0,1,2,3....,M-1
4.3.2取样和频率间隔间的关系
如果f(x)由函数f(t)以△T为单位间隔取样后的M个样本组成,则包含集合{f(x)},x=0,1,2,…,M-1的记录的持续时间是
T=M△T
离散频率域中的相应间隔△u:
由DFT的M个分量跨越的整个频率范围是:
4.4两个变量的函数的扩展
4.4.1二维冲激及其取样特征
两个连续变量t和z的冲激δ(t,z)被定义为如式:
和
如在一维情况那样,二维冲激在积分下呈现了取样特性:
或者,更一般地,对位于坐标(t₀,zo)处的冲激,有:
4.4.2二维连续傅里叶变换对
令f(t,z)是两个连续变量t和z的连续函数。则其二维连续傅里叶变换对由以下两个表达式给出:
4.4.3二维取样和二维取样定理
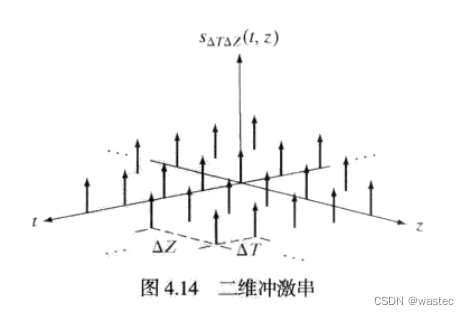
类似于一维情况中的方式,二维取样可用取样函数(二维冲激串)建模:
其中,△T和△Z是连续函数f(t,z)沿t轴和z轴的样本间的间隔。上式描述了沿着两个轴无限扩展的周期冲激的集合(见图4.14)。如图4.5中说明的一维情况那样,
4.4.4图像中的混淆
正如在一维情况下那样,如果只在两个坐标方向上无限扩展,二维连续变量t和z的连续函数通常可以被带限。因为我们不可能对一个函数无限地取样,所以,正像在取样后的一维函数中所存在的那样,在数字图像中混淆总是存在的。在图像中,存在两种主要的混淆现象:空间混淆和时间混淆。空间混淆是由欠取样造成的。时间混淆与图像序列中图像间的时间间隔有关。
4.4.5二维离散傅里叶变换及其反变换
给出变换F(u,v),我们可以使用傅里叶反变换(IDFT)得到f(x,y):
4.5二维离散傅里叶变换的一些性质
4.5.1空间和频率间隔的关系
相应离散频率域变量间的间隔分别由:
和
给出。
4.5.2平移和旋转
下式可以证明傅里叶变换对满足平移特性:
下式满足旋转变化:
4.5.3周期性
如在一维情况中那样,二维傅里叶变换及其反变换在u方向和v方向是无限周期的,即 F(u,v)=F(u+k₁M,v)=F(u,v+k₂N)=F(u+k₁M,v+k₂N)
和
f(x,y)=f(x+k₁M,y)=f(x,y+k₂N)=f(x+k₁M,y+k₂N)
其中,k₁和k,是整数。
4.5.4对称性
函数分析得到的一个重要结果是,任意实函数或虚函数w(x,y)可表示为一个奇数部分和一个偶数部分(其中每一个都可以是实部或虚部)的和:
w(x,y)=w.(x,y)+w₀(x,y)
偶数部分和奇数部分定义如下
和
也就是说,偶函数是对称的,奇函数是反对称的。
4.5.5傅里叶谱和相角
幅度
称为傅里叶谱(或频谱),而
称为相角。
4.5.6二维卷积定理
二维循环卷积的表达式:
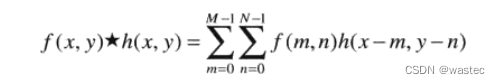
其中,x=0,1,2,…,M-1,y=0,1,2,…,N-1。
二维卷积定理由下面的表达式给出:
![]() 反之,
反之,![]()
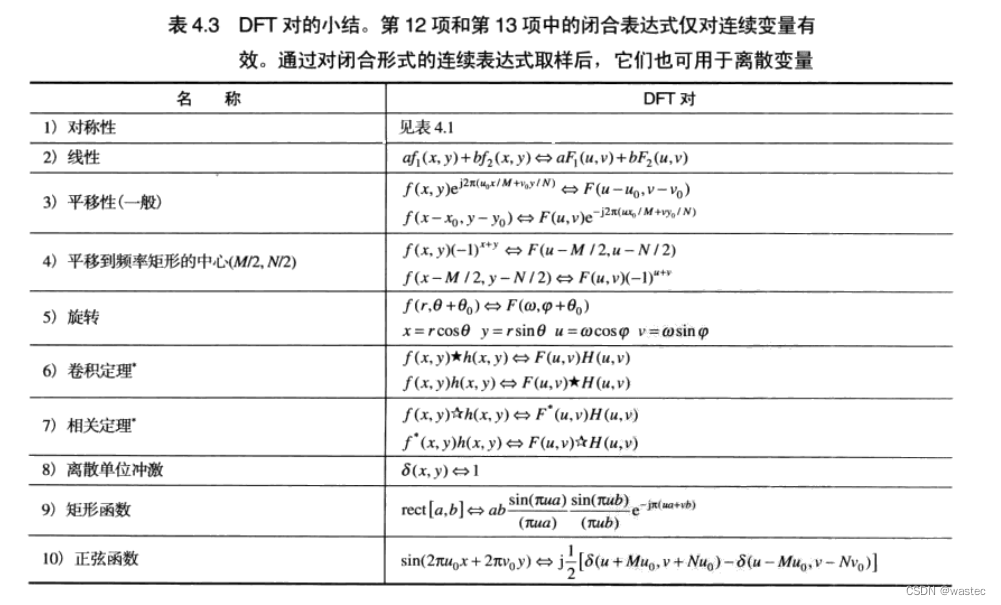
4.5.7二维离散傅里叶变换性质的小结

4.6频率域滤波基础
4.6.1频率域的其他特性
频率直接关系到空间变化率.因此直观地将傅里叶变换中的频率与图像中的亮度变化模式联系起来并不困难。当我们远离变换的原点时,低频对应于图像中变化缓慢的灰度分量。例如,在一幅房间图像中,这些可能对应于墙和地板的平滑灰度变化。当我们从原点移开更远一些时,较高的频率开始对应于图像中越来越快的灰度变化。这些是物体的边缘,或由灰度急剧变化来表征的其他图像分量。
4.6.2频率域滤波基础
频率域滤波由修改一幅图像的傅里叶变换然后计算其反变换得到处理后的结果组成。滤波公式如下:
![]()
其中,是IDFT,F(u,v)是输入图像f(x,y)的DFT,H(u,v)是滤波函数(也简称为滤波器,或者滤波传递函数),g(x,y)是滤波后的(输出)图像。函数F,H和g是大小与输入图像相同的M×N阵列。
4.6.3频率域滤波步骤小结
1.给定一幅大小为M×N的输入图像f(x,y),从式(4.6-31)和式(4.6-32)得到填充参数P和Q。典型地,我们选择P=2M和Q=2N。
2.对f(x,y)添加必要数量的0,形成大小为P×Q的填充后的图像(x,y)。
3.用(-1)*+y乘以f(x,y)移到其变换的中心。
4.计算来自步骤3的图像的DFT,得到F(u,v)。
5.生成一个实的、对称的滤波函数H(u,v),其大小为P×Q,中心在(PI2,Q/2)处①。用阵列相乘形成乘积G(u,v)=H(u,v)F(u,v);即G(i,k)=H(i,k)F(i,k)。
6.得到处理后的图像: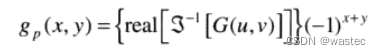 其中,为忽略由于计算不准确导致的寄生复分量,选择了实部,下标p指出我们处理的是填充后的阵列。
其中,为忽略由于计算不准确导致的寄生复分量,选择了实部,下标p指出我们处理的是填充后的阵列。
7.通过从(x,y)的左上象限提取M×N区域,得到最终处理结果
(x,y)。
4.6.4空间和频率域滤波间的对应
给定一个空间滤波器,我们可以用该空间滤波器的傅里叶正变换得到其频率域表示。因此,两个滤波器形成了傅里叶变换对:
其中,h(x,y)是一个空间滤波器。因为该滤波器可以由频率域滤波器对一个冲激的响应得到,所以h(x,y)有时称为H(u,v)的脉冲响应。
4.7使用频率域滤波器平滑图像
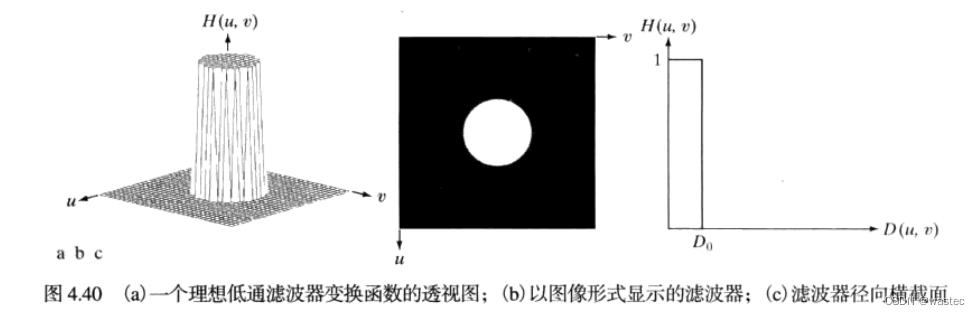
4.7.1理想低通滤波器
在以原点为圆心、以D₀为半径的圆内,无衰减地通过所有频率,而在该圆外“切断”所有频率的二维低通滤波器,称为理想低通滤波器(ILPF);它由下面的函数确定:
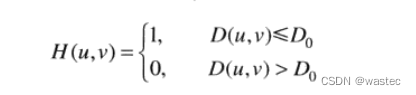
其中,D₀是一个正常数,D(u,v)是频率域中点(u,v)与频率矩形中心的距离,即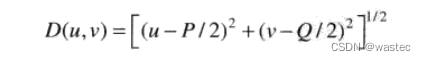
4.7.2布特沃斯低通滤波器
截止频率位于距原点D₀处的n阶布特沃斯低通滤波器(BLPF)的传递函数定义为
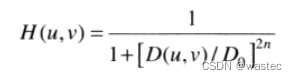
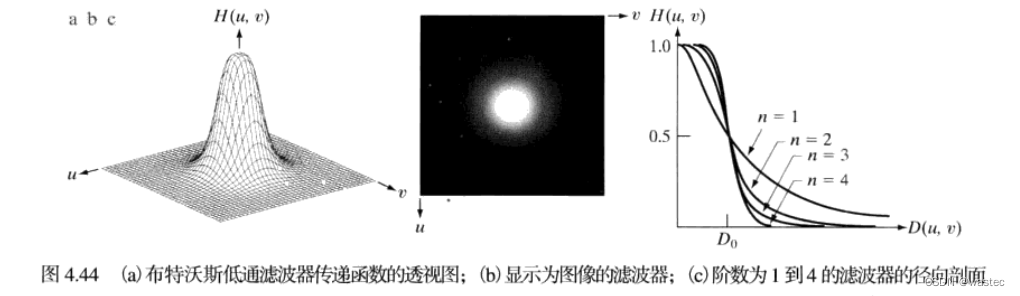
图4.44显示了该BLPF函数的透视图、图像显示和径向剖面图。
4.7.3高斯低通滤波器
一维高斯滤波器的二维形式由下式给出:
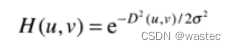
我们可以在本节中使用其他滤波器的表示法来表示该滤波器:
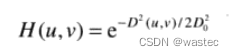

4.7.4低通滤波的其他例子
图4.49显示了一幅低分辨率文本的例子。例如,我们会在传真、复印材料和历史记录中遇到这样的文本。这个特殊的例子中并不存在其他像污点、折痕和破痕这样的困难。图4.49(a)中的放大部分表明该文件中的字符因分辨率不足产生了失真的形状,并且许多字符已断裂。尽管人为填充这些裂缝在视觉上并不困难,但机器识别系统在阅读这些断裂字符时却存在困难。处理这种问题的一种方法是,通过模糊输入图像来桥接输入图像中的这些小裂缝。图4.49(b)显示了如何使用D₀=80的高斯低通滤波器的简单处理图像很好地修复了字符。这些图像的大小为444×508像素。
4.8使用频率域滤波器锐化图像
4.8.1理想高通滤波器
一个二维理想高通滤波器(IHPF)定义为:
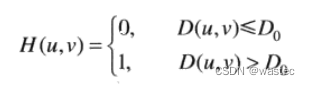
为截止频率
4.8.2布特沃斯高通滤波器
截止频率为D₀的n阶布特沃斯高通滤波器(BHPF)定义为:
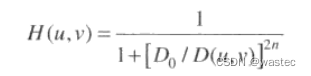
4.8.3高斯高通滤波器
截止频率处在距频率矩形中心距离为D₀的高斯高通滤波器(GHPF)的传递函数由下式给出:
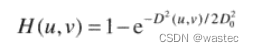

4.8.4频率域的拉普拉斯算子
关于频率矩形的中心,使用如下滤波器:
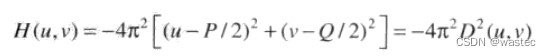
其中,D(u,v)是式(4.8-2)给出的距离函数。然后,拉普拉斯图像由下式得到:
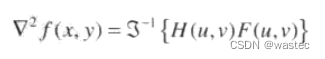
其中,F(u,v)是f(x,y)的傅里叶变换。增强可使用下式实现:
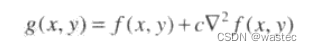
4.8.5钝化模版,高提升滤波和高频强调滤波
下式定义了k=1时的钝化模板和k>1时的高提升滤波器:
![]()
下式定义了高通滤波器:
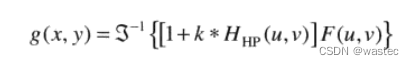
4.8.6同态滤波
在空间域中,滤波后的图像是:
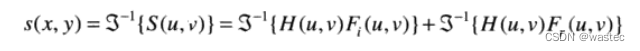
推导的滤波方法总结在图4.60中。该方法是以称之为同态系统的一类系统的特殊情况为基础的。

4.9选择性滤波
4.9.1带阻滤波器和带通滤波器
这种类型的滤波器很容易使用前两节的概念来构建。表4.6给出了理想、布特沃斯和高斯带阻滤波器的表达式,其中D(u,v)是距频率矩形中点的距离,,D₀是带宽的径向中心,W是带宽。图4.63(a)以图像形式显示了一个高斯带阻滤波器,其中黑色是0,白色是1。

一个带通滤波器可以用从低通滤波器得到高通滤波器的相同的方法从带阻滤波器得到:
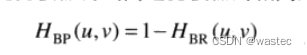
4.9.2陷波滤波器
陷波滤波器是更有用的选择性滤波器。陷波滤波器拒绝(或通过)事先定义的关于频率矩形中心的一个邻域的频率。一般形式为:
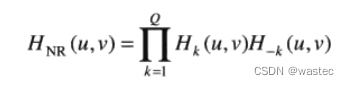
4.10实现
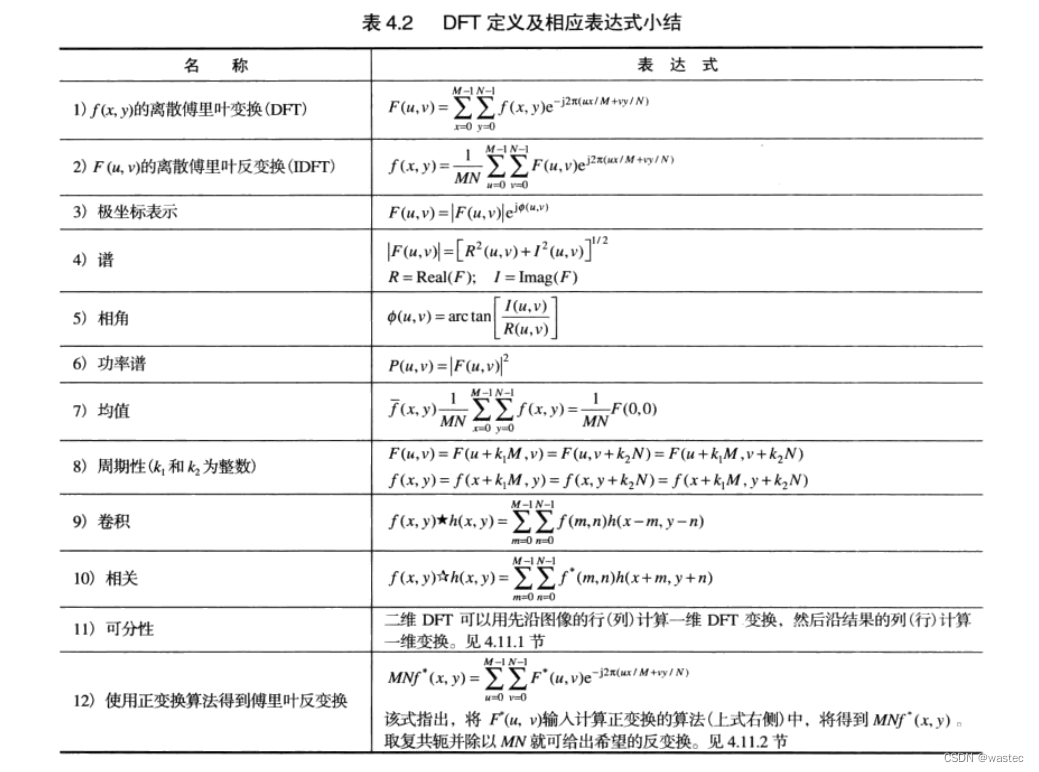
4.10.1二维DFT的可分性
二维DFT可分成一维变换:
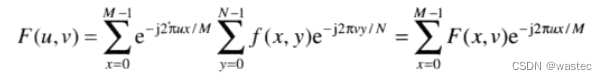
其中:
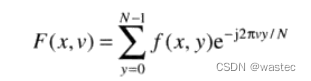
4.10.2用DFT算法计算IDFT
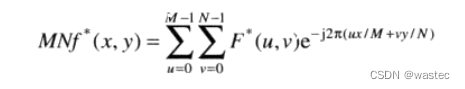
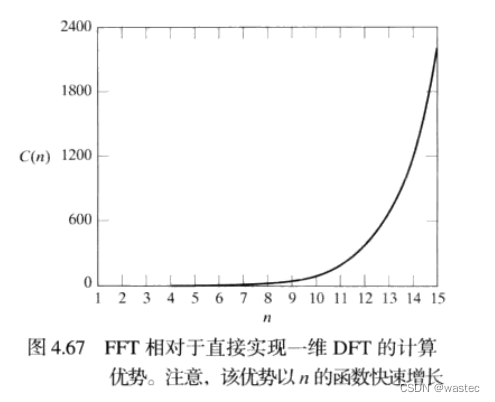
4.10.3快速傅里叶变换(FFT)
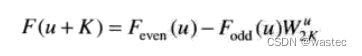





















 5706
5706

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








