点到线段的最短距离——矢量法

矢量算法过程清晰，如果具有一定的空间几何基础，则是解决此类问题时应优先考虑的方法。当需要计算的数据量很大时，这种方式优势明显。

由于矢量具有方向性，故一些方向的判断直接根据其正负号就可以得知，使得其中的一些问题得以很简单的解决。

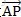
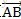
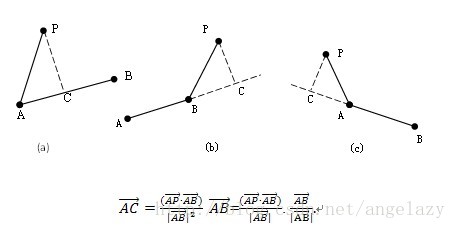
用此方法考虑，我们只需要找到向量 在方向上的投影，具体如下：

 

             

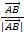
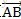
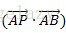
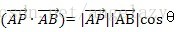
上面的 是方向上的单位向量，其意义是给所求向量确定方向。是的两个向量的内积，且   ，其中θ为向量AP与AB之间的夹角。是向量长度。 

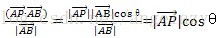
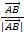
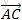
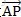
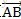
那么即为上图中线段AC的长度值，不带有方向性。此数值与上述表征方向的 整体构成有大小、有方向的新向量，即为 在方向上的投影向量，C为投影点。

根据得到的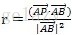，由向量的方向性可知：如果情况是上图（a）所示，那么0<r<1;如果是如图（b）所示的情况，那么r ≥1;如果是如图（c）所示的情况，那么得到r ≤0;

特殊情况如点在线段上、点在端点、点在线段延长线上等等的情况全部适用于此公式，只是作为特殊情况出现，无需另作讨论。这也是矢量算法思想的优势所在。

故根据r值的不同，最短距离

         (r 为 |AC|与|AB|的长度比)

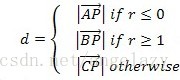
转自：https://www.cnblogs.com/lyggqm/p/4651979.html