循环冗余码CRC可不可以纠错

 循环冗余码CRC

原则:模2除

加密时:首先被模数后面先补最高次数(n-1)位0，模生成多项式n位，异或被模数，取最后余数n-1位，最后余数覆盖数据后面补的0。

检验时，对加密后的数据进行模2除，据余数情况决定对错，0无错。

其实我们一般就是讨论余数是否为0，决定数据是否有错，0无错；不为0有错，删除并要求重传。

 举例：

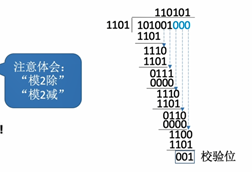
循环冗余码CRC有无纠错能力讨论

举例：

模生成多项式1101

 循环冗余就是会按接受数的的变化，余数随之变化，一般会重复有规律地循环出现，如上图。

满足什么情况才可以检错？

它又来了，2^r>=m+r+1，生成多项式满足r的条件即可。

这个限制可以让余数不会重复出现了，实现余数情况可与（>=）出错位置的一一对应即可检错，映射即可解决。

具体是什么样不纠结，我功力不够，我还没搞懂r与纠错理论中码距的关系。

思路有了，还要列表，麻烦，，但是不考细节，不纠结了。

参考这篇文章你会更加明晰：肝了这篇计组与计网大杂烩奇偶校验，汉明码(海明码)与循环冗余码CRC做题不迷茫---异或的魔力_weilaidedakejilu的博客-CSDN博客注：(通过后面了解，先猜想取等号时：r就是L海明距离，留个坑)n=m+r公式严格满足条件：2^r>=m+r+1(m为真值位数，r校验位数);Hn(1...n):加密后数据内容的带位序常量;(默认小端存储Hn(n...1)在机器中的排列)Dm(1...m):真值的带位序常量;P(2^(0...r)):校验值的带位序常量,作用：加密时，检验一组的1的个数是否符合要求(偶校验||奇校验).S(2^(0...r)):校验值的带位序常量,作用：解密时，检验一组的1的个数是否符合要求(偶校验|https://blog.csdn.net/weilaidedakejilu/article/details/120210241?spm=1001.2014.3001.5501