大学数学中的1和0、求根公式相关和待定系数法

1.反常积分收敛临界判断

2.微分等等

1.在x=0处可导，代表是x的高阶无穷小函数即可，即幂>=1。

2.对1积分，表示求积分区域的最高维度的几何意义（位移，面积，体积

；曲线有：曲线长，曲面面积，曲体体积）

3.任何等式都可以写成1*f(x)=f(x)

常用于公式泛化

4.(cosx)^2+(sinx)^2=1

5.等价无穷小，比值为1；

6.纯正项（负项）的数列比较大小，作除法

3.导数相关

反函数：f(x)’*f[x^(-1)]’=1

垂直：k1*k2=-1

另一种垂直：两个方向向量内积=0

4.概率论

分布律累加=1

概率分布函数(如标准正态分布)<=1

特别的：pi^0.5

相关公式：正相关时：ρ=1

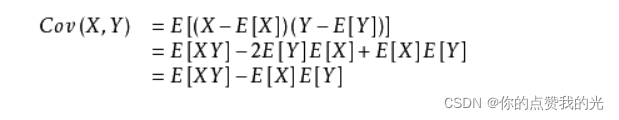
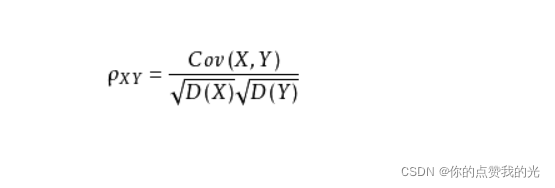
置信度1-α,F(?)表示标准正态分布的分布函数

F(?)+α/2=1

F(?)一般由题目给出

6.不相关---0

线性无关

变量相互独立或者说简单随机样本

5求根公式相关

验证公式：AC-B^2无条件极值：用求根公式的验证公式的负数形式表示，正有负不一定

求根公式：二阶线性微分方程的通解对应形式，有解无解都有对应公式

6.待定系数法

拆分原则中有待定系数法，待定每一项都符合阶数为-1阶

二阶线性微分方程中也有待定系数法，等式右边待定为特解形式，形式与特解情况相关。