同济高等数学：第一章第二节 数列的极限

本小节我们主要把目光聚焦在数列极限的定义上面，以及如何利用定义证明极限存在。最后简单介绍下收敛数列的性质。

一、数列极限的定义

这个定义是令很多学习者头大的事情。接下来我们主要对这个定义加以解释。

首先我们得知道，数列的极限解决的是什么问题？

注： 两个数之间的接近程度可以用两个数之间差的绝对值来表示。差的绝对值越小，这两个数就越接近。

那么对于

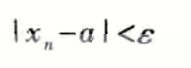
的解释就迎刃而解。

它表示就是数列的第n项与极限值之间的距离。这个距离小于任意给定一个正数具体来说呢，这个符号表示一个任意的，特别小的正数。

那么文字表述就是，数列第n项与极限值的距离小于一个任意给定的特别小的正数。这就表明数列已经很接近极限。