mandelbrot_Swift强大的运算功能，Mandelbrot的分形艺术-iOS

最新推荐文章于 2024-10-14 23:40:45 发布

weixin_26638123

最新推荐文章于 2024-10-14 23:40:45 发布

阅读量377

点赞数

文章标签： python

原文链接：https://medium.com/swlh/mandelbrots-fractal-art-with-swift-s-powerful-computation-ios-5d48f337b094

版权

本文介绍如何利用Swift的强大计算能力来创建Mandelbrot分形图像，展示了iOS平台上的分形艺术实现。

摘要由CSDN通过智能技术生成

mandelbrot

Fractal is a pattern, which is generated by kind of specific math iterations recursively. These are infinitely generated complex patterns that are self-similar across different scales. They are generated by repeating a process over and over in an ongoing feedback loop. So, because of this recursion process, there is something beautiful, chaotic patterns are generated.

分形是一种模式，它是由某种特定的数学迭代递归生成的。这些是无限生成的复杂模式，它们在不同尺度上是自相似的 。它们是通过在不断进行的反馈循环中反复重复一个过程而生成的。因此，由于此递归过程 ，会产生一些美丽的混乱模式。

Self-similar means when you zooming in the pattern with recursion of iteration, the same kind of base pattern is visualized at many intervals. And this process is infinite. There is no end. Just look at the below example.

自相似意味着通过迭代递归放大模式时，会以许多时间间隔显示相同类型的基本模式。这个过程是无限的。没有尽头。只要看下面的例子。

This animation is just an example of some kind of recursive math iterations, which tends to generate this, and this could be any type of pattern which depends upon the geometric plane, and math calculations.

此动画只是某种递归数学迭代的示例，往往会生成这种动画，并且这可以是取决于几何平面和数学计算的任何类型的模式。

Scientists and mathematicians like Benoit Mandelbrot say that these patterns geometrically exist between dimensions in which we are leaving. Fractals are existing everywhere like trees, rivers, coastlines, mountains, clouds, seashells, hurricanes, etc.

像Benoit Mandelbrot这样的科学家和数学家说，这些模式在几何形状上存在于我们要离开的维度之间。分形随处可见，例如树木，河流，海岸线，山脉，云层，贝壳，飓风等。

There is a movie on the great Indian mathematician Ramanujan, “The Man Who Knew Infinity”, in which he is saying that the patterns are everywhere.

印度伟大的数学家 拉马努让(Ramanujan)上有一部电影， “知道无限的人” ，他在电影中说到处都有图案。

There is little conversation between him and her wife in the movie.

电影中他和妻子之间几乎没有对话。

Srinivasa Ramanujan: What do you see?Janaki: Sand.[he picks up a handful of sand]Srinivasa Ramanujan: Imagine if we could look so closely we could see each grain, each particle. You see there are patterns in everything. The color in light, the reflection in the water. In maths that patterns reveals them selves in incredible form.

Srinivasa Ramanujan：您看到什么？ Janaki：沙子。[他捡了几块沙子] Srinivasa Ramanujan：想象一下，如果我们看得这么近，我们可以看到每个颗粒，每个颗粒。您会看到一切都有模式。颜色在光线中，在水中反射。在数学中，模式以难以置信的形式揭示了自我。

L

大号

递归函数 (Recursive function)

A recursive function is familiar terms for developers. Below is an example.

递归函数是为开发人员熟悉的术语。下面是一个例子。

The below example is a quadratic polynomial function in maths.

下面的示例是数学中的二次多项式函数。

f(x) = x² + 1

f(x)=x²+ 1

Iterate the above function 3 times from 1 to 3. As an input value x provides the last iteration result.

从1到3迭代上述函数3次。输入值x提供最后的迭代结果。

f(1) = 1 + 1 = 2

f(1)= 1 +1 = 2

f(2) = 4 + 1 = 5

f(2)= 4 +1 = 5

f(3) = 25 + 1 = 26

f(3)= 25 +1 = 26

Imagine if we will do the above process 100, 1000, or more times, what will be the result. We will get a large number.

想象一下，如果将上述过程进行100、1000或更多次，结果将是什么。我们将得到大量。

It’s obvious that we can not calculate that iteration on paper, and we required a computer for this. And computation time for this or any kind of math calculation depends upon the processor, efficiency of the language, and proper algorithm.

我 T的明显，我们不能指望着纸张迭代，我们需要一台计算机此。而这种或任何种类的数学计算的计算时间取决于处理器，语言的效率和适当的算法 。

With iterating this kind of simple function so many times we can generate the fractals on a complex plane. And we can zoom in to infinite level, the pattern never ends.

通过多次迭代这种简单函数，我们可以在复杂平面上生成分形。而且我们可以放大到无限的水平，图案永无止境。

We will generate this below amazing pattern in the iOS by using swift code. This pattern also follows the rule of self-similarity as discussed above.

我们将使用Swift代码在iOS中生成以下惊人的模式。该模式还遵循如上所述的自相似性规则。

So, before start understanding just refer to this below link where you can zoom in and out the pattern at any point by just clicking the right and left button. It will make you amaze. Try it.

因此，在开始理解之前，请参考下面的链接，您可以在其中通过单击左右按钮随时放大和缩小图案。这会让你惊讶。试试吧。

http://xaos-project.github.io/XaoSjs/

http://xaos-project.github.io/XaoSjs/

That same thing we will do in the swift with the fraction of code. The same pattern and same zoom level with a variety of different colors in the pattern. We can zoom in but we are not able to animate it, as our code takes a few seconds for iterating the function, filling color as per device’s display size. Get the full project here. https://github.com/Dhaval1094/DUMendelbrot-Swift

我们将与代码的分数Swift做T的帽子同样的事情。相同的图案和相同的缩放级别 ，其中图案具有多种不同的颜色 。我们可以放大，但无法对其进行动画处理，因为我们的代码需要花费几秒钟来迭代该功能，并根据设备的显示尺寸填充颜色。在此处获取完整的项目。 https://github.com/Dhaval1094/DUMendelbrot-Swift

But what is that Mandelbrot set???

但是曼德尔布洛特是做什么的呢？？？

The Mandelbrot set is the set of all complex numbers that will not explode to infinity when the equation below is iteratively applied to them so many times.

Mandelbrot集是所有复数的集合，当以下方程式对其多次迭代应用时，它们不会爆炸到无穷大。

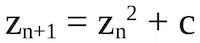
We are placing a complex number denoted as C in the equation. Then after applying the iteration recursively.

我们在方程式中放置一个表示为C的复数。然后递归应用迭代后。

We can imagine that the resulted value will be bigger and bigger, but for a few complex numbers, this is not true. Means for a few complex numbers the iteration result will be remain between -2 and 1. So, we got two conditions here.

我们可以想象得到的值会越来越大，但是对于一些复杂的数字，事实并非如此。对于一些复数的均值，迭代结果将保持在-2和1之间。因此，我们在这里有两个条件 。

第一个条件 (First condition)

After a few iterations, the value is escaping from -2 and 1. And if we iterate more and more this iterations result will tend to infinity.

经过几次迭代后，该值将从-2和1转义。如果我们进行越来越多的迭代，则迭代结果将趋于无穷大。

Conclusion: This kind of complex number is not considered as a part of the Mandelbrot set, and it’s outside the set.

结论：这种复数不被视为Mandelbrot集的一部分，而是在集之外。

第二条件 (Second condition)

After so many iterations, the value is not escaping from -2 to 1, the result of all iterations will remain between these two values. No matters how many times we are iterating this equation recursively.

经过如此多次的迭代后，该值并未从-2到1转义，所有迭代的结果将保留在这两个值之间。不管有多少次我们递归地迭代这个方程。

Conclusion: This kind of complex number is a part of the Mandelbrot set and it’s inside the set.

结论：这种复数是Mandelbrot集的一部分，位于集内。

That’s the logic behind the Mandelbrot set.

这就是Mandelbrot集背后的逻辑。

For understanding how to generate this Mandelbrot Set with programming, knowledge of a few math terms are a prerequisite.

要了解如何通过编程生成此Mandelbrot集，必须具备一些数学术语的知识。

Real Numbers
实数
Imaginary Numbers
虚数
Complex Numbers
复数
Complex Plane
复杂平面
The calculation for adding and multiplying two complex numbers
两个复数相加和相乘的计算

实数 (Real Numbers)

Simply, these below are the real numbers.

简而言之，以下是真实数字。

0,1,2,3,4,5………n

0,1,2,3,4,5………n

-1,-2,-3,-4,-5……..-n

-1，-2，-3，-4，-5……..- n

虚数 (Imaginary Numbers)

Let’s take an equation x² +1 = 0. The answer will become x² = -1. So, we can write x = √-1. But in maths, there is no possible root of any negative number. Few scientific calculators give an error if we enter √-1 and click on the equal button. Even google calculator gives an error.

让我们考虑一个方程x²+1 =0 。答案将变为x²= -1 。因此，我们可以写成x =√-1 。但是在数学中，不可能有任何负数的根。如果输入√-1并单击相等按钮，几乎没有科学计算器会给出错误。甚至Google计算器也给出了错误。

But according to Euler's imaginary number theory, that does not mean the number does not exist. He gives the symbol i for the value √-1 an imaginary number like 1i, 2i, 3i, and so on. As an example take √-9. Then it’s called 3i.

但是根据欧拉的虚数理论，这并不意味着该数不存在。他给值√-1的符号i一个虚数，例如1i，2i，3i等。以√-9为例。然后称为3i。

√-9 = √9*√-1 = 3√-1 = 3i

√-9=√9*√-1=3√-1= 3i

Where 3 is a real number and i mean √-1 is an imaginary number. So, it’s a combination of real and imaginary numbers.

其中3是实数，我的意思是√-1是虚数。因此，它是实数和虚数的组合。

复数 (Complex Numbers)

Complex numbers are the addition of a real number and imaginary number. It will look like this.

复数是实数和虚数的加法。它看起来像这样。

4 + 3i , 5 + 2i , 1 + 6i

4 + 3i，5 + 2i，1 + 6i

复杂平面 (Complex Plane)

Simply in the normal graph, there are real numbers on both x and y-axis. But in the complex plane, there are real numbers on the x-axis and imaginary numbers on the y-axis. So if we take any point on the graph with x and y, (x+y) it will become a complex number. That means at each point on the complex plane we will get it’s complex number accordingly.

仅在法线图中，x和y轴上都有实数。但是在复平面中， x轴上有实数，y轴上有 虚数。因此，如果我们用x和y(x + y)取图上的任何点，它将变成复数。这意味着在复平面上的每个点上，我们都会相应地得到它的复数。

There is a Mendalbrot’s iterative function which we will use in code for generating mandelbrot pattern.

有一个Mendalbrot的迭代函数，我们将在代码中使用该函数来生成mandelbrot模式。

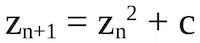
Here Zn starts from 0 and c is complex number. It could be any complex number i.e. a+bi.

此处 Zn 从 0 开始， c 为 复数。 它可以是任何复数，即 a + bi 。

如何生成Mandelbrot集？ (How to generate Mandelbrot set?)

Zn = Zn² + c

锌=锌2 + c

Z1 = (0)² + c

Z1 =(0)²+ c

Z2 = (c)² + c

Z2 =(c)² + c

Now as we know that c = a + bi => c² = (a+bi)².

现在我们知道c = a + bi =>c²=(a + bi)²。

If we factories (a + bi)² then the result will be as below.

如果我们工厂( a + bi)²，则结果将如下所示。

(a²-b²) + 2abi, where (a²-b²) is real number and 2abi becomes our complex number.

(a²-b²)+ 2abi， 其中 (a²-b²) 是实 数，而 2abi 是我们的 复数。

So, the main steps we have to do in the programming are —

因此，我们在编程中要做的主要步骤是-

第1步 (Step — 1)

Take a UIView subclass for drawing the pattern and name the class, MendalbrotView.

以UIView子类来绘制模式，并将其命名为MendalbrotView 。

第2步 (Step — 2)

Make a model for store real and imaginary numbers.

为存储实数和虚数建立模型。

步骤— 3 (Step — 3)

We have to convert the normal view rect into a Complex rect. Create a model class for the complex plane. In short, we have to make a graph that contains complex coordinates.

我们必须将法线视图rect转换为Complex rect。为复杂平面创建模型类。简而言之，我们必须制作一个包含复杂坐标的图。

Because the mandelbrot view remains between these two points (x: -2.1, y: 1.5) and (x: 1, y: 1.5), we have to make rect between these values.

因为mandelbrot视图保持在这两个点(x：-2.1，y：1.5)和(x：1，y：1.5)之间 ，所以我们必须在这两个值之间进行校正。

第4步 (Step — 4)

Calculate the view size and, convert the view in the complex plane. Now that’s the tricky one. We know that on the x-axis there are real numbers and on the y-axis, there are imaginary numbers.

计算视图大小，然后在复杂平面中转换视图。现在那是棘手的。我们知道在x轴上有实数，在y轴上有虚数。

Assume that we have a UIView with this below rect.

假设我们有一个UIView与这个下面的矩形。

CGRect(x: 0, y: 0, width: 375, height:375)

CGRect(x：0，y：0，宽度：375，高度：375)

So, in this case, if we count pixel size 1, then there are 375*375 = 1,40,625 CGPoints on this view.

因此，在这种情况下，如果我们计算像素大小1，则此视图上有375 * 375 = 1,40,625 CGPoints 。

Now we want four complex numbers to make a complex rect. And the thing is we have also a zoom scale. According to which we have to change the real rect into complex rect. This means that when we do zoom in the CGRect(x: 0, y: 0, width: 375, height:375) the origins of this CGRect will remain the same but the origin of the converted complex plane will be lesser and lesser.

现在我们想要四个复数组成一个复数矩形。而且，我们还有一个缩放比例。据此，我们必须将实际rect更改为复数rect。这意味着当我们放大CGRect(x：0，y：0，宽度：375，高度：375)时 ，此CGRect的原点将保持不变，但转换后的复杂平面的原点将越来越少。

步骤— 5 (Step — 5)

Create a loop for all complex coordinates in the view.

为视图中的所有复杂坐标创建一个循环。

步骤— 6 (Step — 6)

Convert each x and y value to a complex coordinate.

将每个x和y值转换为复数坐标。

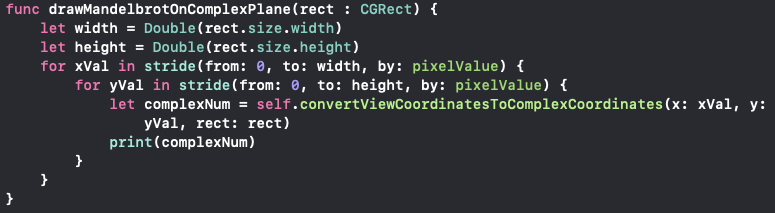
步骤— 7 (Step — 7)

Implement the mandelbrot equation on the converted complex number for particular x and y value inside the for-loop.

在for循环内，对转换后的复数实现特定x和y值的mandelbrot方程。

According to mendlabrot’s law if the iteration result is more than 2 for the current complex number the result of next iterations are reach towards infinity, means this complex number is not part of the Mandelbrot set and returns white color for that particular coordinate, and if the value is less than 2 after 100 iterations means that the value of next iterations results will remain between 0 and 2. No matters how many times we iterate this equation, but the result of all iterations will remain between 0 and 2. That means this complex number is part of the Mandelbrot set. So, it will return the black color for this particular complex number.

根据Mendlabrot定律，如果当前复数的迭代结果大于2 下一次迭代的结果接近无穷大 ，这意味着该复数 不是Mandelbrot集的一部分，并且会为该特定坐标返回白色，并且如果在100次迭代后该值小于2，则意味着下一次迭代的 结果将为保持在0到2之间 。不管迭代这个方程多少次，但是所有迭代的结果都将保持在0到2之间 。这意味着该复数是Mandelbrot集的一部分。 因此，它将为此特定复数返回黑色。

步骤— 8 (Step — 8)

We got these below 2 required things in the for loop with which we can fill UIBezierPath with black or white color.

我们在for循环中获得了以下2项必需的东西，用它们可以用黑色或白色填充UIBezierPath 。

The fill color of the coordinate
坐标的填充颜色
The x and y value we have already for that particular complex coordinate
对于特定的复数坐标，我们已经有了x和y值

That’s it.

而已。

After implementing this code and run the application we will get the below black and white-colored mandelbrot view on the display.

在执行此代码并运行应用程序之后，我们将在显示屏上看到下面的黑白mandelbrot视图。

Now the final step — fill colors for making the pattern attractive like in the above video. So, we have to make an array of different colors, and we will use this array for set fill color for a particular coordinate.

现在， 最后一步 -像上面的视频中那样填充颜色以使图案更具吸引力。因此，我们必须制作一个不同颜色的数组，并将此数组用于设置特定坐标的填充颜色。

步骤— 9 (Step — 9)

We keep iteration count 100, which means we will iterate te mandelbrot equation 100 times, and if it’s outside the Mandelbrot set we will select a particular color for that particular coordinate.

我们将迭代计数保持为100，这意味着我们将对mandelbrot方程进行100次迭代，如果它不在Mandelbrot集中，我们将为该特定坐标选择特定颜色。

So we have 100 possible colors to fill in the outside coordinates.

因此，我们有100种可能的颜色来填充外部坐标。

After initializing colors we can perform the iteration and return particular color for the iteration result.

初始化颜色后，我们可以执行迭代，并为迭代结果返回特定的颜色。

After implement of the colors, the final colored mandelbrot view is prepared. It will look like below.

实施颜色后，将准备最终的有色曼德布罗特视图。如下所示。

The three sets are with different colors because we initialize random colors every time when we initialize the Mandelbrot view.

这三组具有不同的颜色，因为每次初始化Mandelbrot视图时都会初始化随机颜色。

We can do some modification and implement functionalities for this view i.e. zoom in the view at particular coordinates, change colors, enlist the values of complex numbers inside the set, and outside the set, get total iteration counts and time for the screen size, the clarity with a pixel value.

我们可以对此视图进行一些修改和实现功能，即在特定坐标处放大视图，更改颜色，在集合内和集合外获取复数的值，以获得总的迭代次数和屏幕尺寸的时间，像素值的清晰度。

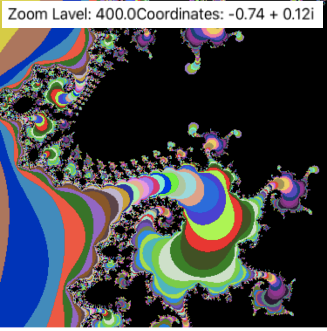
The below image shows these all things which we can do with the Mandelbrot set.

下图显示了我们可以使用Mandelbrot集进行的所有操作。

With zooming at the particular coordinate, new patterns are created. No matter how much we are zooming. With 1.4 zoom level, you get the full image of Mandelbrot set, and with the zoom level 1000000000, you will get the part of particular coordinate and beautiful patterns around it. You can zoom 10^n times. There is no end as in the video 😁. Coordinate is a particular complex number, which we are using to apply in the equation. So, that coordinates in the below images are the C value in the equation.

通过缩放特定的坐标，可以创建新的图案。无论我们缩放多少。使用1.4缩放级别，您将获得Mandelbrot集的完整图像，使用1000000000缩放级别，您将获得其周围特定坐标和精美图案的部分。您可以放大10 ^ n倍。没有视频😁中的结尾。坐标是一个特定的复数，我们将其应用到方程中。因此，以下图像中的坐标为方程式中的C值。

That’s the full story about creating fractals with Mandelbrot set. But the other main thing is that the power of swift computation makes it possible to generate this kind of fractal on iPhone or iPad. As we mention in the title Swift’s powerful computation.

牛逼的帽子是关于与Mandelbrot集分形创建完整的故事。但另一个主要问题是，快速计算的功能使在iPhone或iPad上生成这种分形成为可能。正如我们在标题中提到的， Swift的强大计算能力 。