数据结构二叉排序树建立
In everyday life, we need to find things or make decisions, and one way to make that process easier is to cut those choices in half.
在日常生活中,我们需要找到事情或做出决定,而简化这一过程的一种方法就是将这些选择减少一半。
Let’s say you’re playing a round of the board game Guess Who? where the object of the game is to guess the character your opponent has selected. You might ask them questions like:
假设您正在玩一局棋盘游戏, 猜猜谁? 游戏的目标是猜测对手选择的角色。 您可能会问他们一些问题,例如:
Is your person a male or a female?
您的人是男性还是女性?
Male. Ok, does he have facial hair?
男。 好吧,他有胡子吗?
No. Ok, is he wearing a hat?
好的,他戴着帽子吗?
We continue to deduce our choices with every step. After all, there’s no need to consider all those women or mustachioed men if you know you’re looking for a clean-shaven man! In a similar way, binary search trees allow us to find what we’re looking for by reducing our options at every step.
我们会一步一步地推断出我们的选择。 毕竟,如果您知道正在寻找一个剃光洁面的男人,则无需考虑所有那些女性或大胡子男人! 以类似的方式,二叉搜索树使我们可以通过减少每一步的选择来找到所需的内容。
首先,二叉搜索树到底是什么? (First of all, what the heck is a binary search tree?)
A binary search tree (BST) is a special type of tree data structure made up of nodes and their descendants, which are also known as ‘children’. You can imagine this either like an upside down tree or the roots of a tree.
二叉搜索树(BST)是一种特殊类型的树数据结构,它由节点及其后代(也称为“子代”)组成。 您可以想象这就像倒立的树还是树的根。
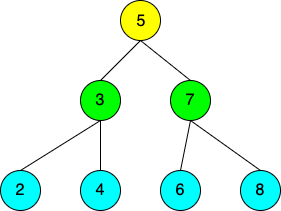
Each node can only have a maximum of 2 children: a left node and a right node. The left node value must always be less than the parent node, and the right node value must always be greater, in order for it to be a valid binary search tree. A BST without any gaps, where each node has both a left and right descendent, is known as a “perfect” tree.
每个节点最多只能有2个子节点:左节点和右节点。 左节点的值必须始终小于父节点的值,而右节点的值必须始终大于父节点的值,以使其成为有效的二进制搜索树。 一个没有间隙的BST,每个节点都有左右后代,被称为“完美”树。
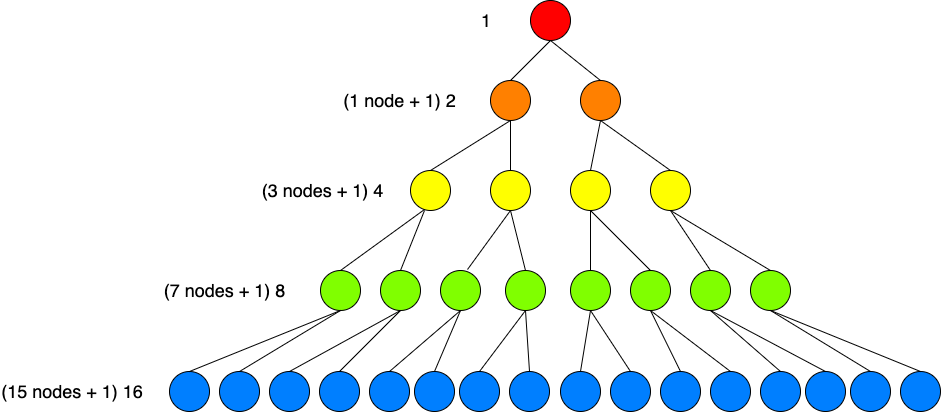
In a perfect tree, the number of nodes in each level doubles as you traverse down the tree. Additionally, you can find the total number of nodes on the bottom level by adding up all of the previous nodes and adding an additional “1” to that number.
在一棵完美的树中,当您遍历树时,每个级别中的节点数都会加倍。 此外,您可以通过将所有先前的节点相加并在该数目上添加一个额外的“ 1”来找到底层节点的总数。
When we search for an element in a balanced binary search tree, it takes O(log n) time on average, and in the worst case scenario, O(n). You can think of searching through a BST as a “Choose your own adventure” model starting at the top node and continuing down the tree, asking the same 2 questions at each node you arrive on.
当我们在平衡二叉搜索树中搜索元素时,平均花费O(log n)时间,在最坏的情况下,则花费O(n) 。 您可以考虑将BST搜索作为“选择自己的冒险”模型,该模型从顶部节点开始,一直到树下,在到达的每个节点上都问同样的2个问题。
Is the value that I’m looking for less than the current node? If so, go left.
我要查找的值是否小于当前节点? 如果是这样,请向左走。
Is the value that I’m looking for greater than the current node? If so, go right.
我要查找的值是否大于当前节点? 如果是这样,请继续。
They’re also pretty fast for insertions or deletions, taking O(log n) time on average. One downside is that you can’t get random element access like you can with an array.
它们对于插入或删除也非常快,平均花费O(log n)时间。 缺点是您无法像使用数组那样获得随机元素访问。
什么时候使用二叉搜索树? (When would you use a binary search tree?)
Let’s say you were asked to design a database for a social media app like Facebook. You know that your database will need to handle millions of usernames, and it will need to quickly retrieve one during login. Since people sign up or delete their accounts every day, you will also need easy access to make those insertions and deletions.
假设您被要求为社交媒体应用(如Facebook)设计数据库。 您知道您的数据库将需要处理数百万个用户名,并且需要在登录期间快速检索一个用户名。 由于人们每天都在注册或删除他们的帐户,因此您还需要易于访问才能进行这些插入和删除操作。
We know that binary search through a sorted array would be pretty fast (O(log n)), but in order to insert or delete a username, the entire array would need to be re-sorted taking O(n) time which, depending on the size of your array, could be a bit slow. If we were to use a BST instead, this insertion/deletion time becomes much faster (O(log n)).
我们知道通过排序数组进行二进制搜索会非常快(O(log n)),但是为了插入或删除用户名,整个数组将需要花费O(n)时间重新排序,具体取决于在您的阵列大小上,可能会有点慢。 如果我们改为使用BST,则此插入/删除时间会变得更快(O(log n))。

If we were to have a binary search tree with names (such as in this skillfully-crafted Finding Nemo tree I’ve made 😊), the tree could be organized alphabetically.
如果我们要有一个带有名称的二叉搜索树( 例如,在 我 精心制作的 这个 精心制作的“ 海底总动员”树中, 😊),则该树可以按字母顺序组织。
“Dory” comes before “Marlin” in the alphabet so she’s the left node, and “Nigel” comes after Marlin so he goes to the right. The same process is repeated as we venture down each level. “Bruce” comes before “Crush”, and before Dory and Marlin. “Darla” comes after Crush, but still before Dory and Marlin.
“ Dory”在字母表中的“ Marlin”之前,因此她是左侧节点,“ Nigel”在Marlin之后,因此他位于右侧。 当我们冒险降低每个级别时,将重复相同的过程。 “布鲁斯”出现在“暗恋”之前,多莉和马林之前。 “ Darla”出现在Crush之后,但仍然出现在Dory和Marlin之前。
Now get ready, because it’s time to find Nemo! 🕵️♀️
现在准备好,因为是时候找到Nemo了! 🕵️♀️
找到尼莫! (Find Nemo!)
Let’s say that we already know we have a valid binary search tree and we need to find Nemo. Since we know that the nodes in our tree are sorted alphabetically, this should be fairly simple.
假设我们已经知道我们有一个有效的二进制搜索树,并且需要找到Nemo。 由于我们知道树中的节点是按字母顺序排序的,因此这应该非常简单。
Starting from Marlin, we have Dory to the left and Nigel to the right. We know that Nemo comes after Marlin in the alphabet, so we would traverse to the right node (Nigel). We know that Nemo comes after Nigel alphabetically, so we continue down to Nigel’s right descendent. Lucky for us, that happens to be…NEMO! You found Nemo! 🥳
从马林出发,左边是Dory,右边是Nigel。 我们知道Nemo在字母中紧随马林之后,因此我们将遍历到正确的节点(Nigel)。 我们知道Nemo按字母顺序排在Nigel的后面,因此我们继续讲到Nigel的右后裔。 对我们来说幸运的是,那是……NEMO! 您找到了尼莫! 🥳

Well that was efficient. Thanks binary search tree, you cut our entire search down with O(log n) time complexity! 👍
好吧,那很有效。 感谢二叉搜索树,您以O(log n)的时间复杂度削减了我们的整个搜索! 👍
Now what if our tree wasn’t sorted at all, and was just a regular tree structure? OR what if we’re asked to validate that we have a binary search tree? There are 2 different search techniques that can help with that.
现在,如果我们的树根本没有排序,而只是常规的树结构怎么办? 或者,如果要求我们验证是否拥有二叉搜索树,该怎么办? 有2种不同的搜索技术可以帮助您解决问题。
什么是广度优先搜索? (What is breadth-first search?)
Breadth-first search is a way of traversing through a tree (or graph) one level at a time, moving across the nodes from left to right.
广度优先搜索是一次遍历一棵树(或图),从左到右跨节点移动的一种方式。
In our Finding Nemo example, Marlin would first check with Dory, asking “Do you know where my son, Nemo, is?” If she says no, he would then ask Nigel the same question. If Nigel also says no, Marlin would move down one level and ask Crush, Gill, Mr. Ray, and then… Nemo! He found Nemo! 🎉
在我们的Finding Nemo示例中,Marlin首先向Dory询问,“您知道我的儿子Nemo在哪里吗?” 如果她拒绝,他会问奈杰尔同样的问题。 如果奈杰尔(Nigel)也拒绝,那么马林(Marlin)会下移一个层次,问卡什(Crush),吉尔(Gill),雷先生(Ray),然后……尼莫! 他找到了尼莫! 🎉
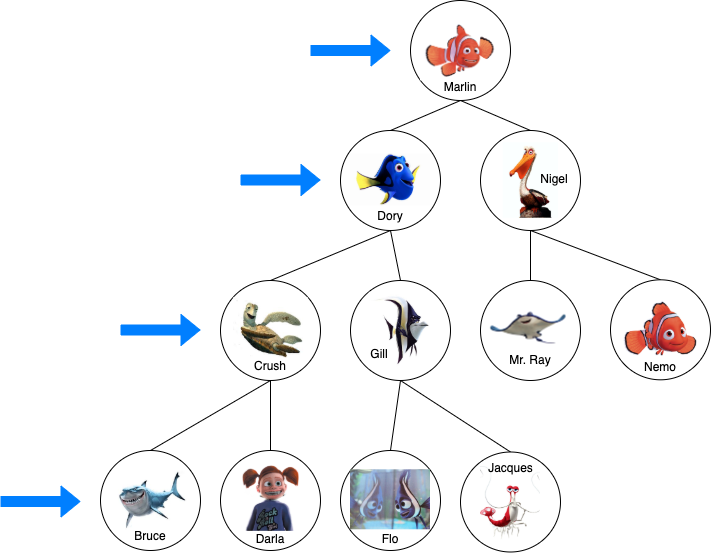
If Nemo wasn’t located after Mr. Ray, Marlin would have continued down to the next level, asking Bruce, Darla and so on.
如果Nemo不在Ray先生之后,那么Marlin会继续走下一个台阶,问Bruce,Darla等。
Using breadth-first search will allow you to find the shortest possible distance between the starting node (Marlin) and the one you’re looking for (Nemo!). The time complexity is O(n) because at worst, you would need to check every single node to find Nemo.
使用广度优先搜索将使您能够找到起始节点(Marlin)与所需节点(Nemo!)之间的最短距离。 时间复杂度为O(n),因为在最坏的情况下,您需要检查每个节点才能找到Nemo。
什么是深度优先搜索? (What is depth-first search?)
Depth-first search is a way of traversing through a tree (or graph) from the top node all the way down to its furthest descendant, and then backing up and trying another path if the node you’re searching for isn’t found.
深度优先搜索是一种从顶部节点一直到最远的后代遍历一棵树(或图形)的方法,如果找不到要搜索的节点,则进行备份并尝试另一条路径。
In our Finding Nemo example, Marlin would first check with Dory, asking “Do you know where Nemo is?” If she says no, he would then ask Crush the same question since Crush descends from Dory on the left-most path. If Crush also says no, Marlin would move down one level to Bruce and, although terrified of becoming a shark snack 😰, would ask him if he’s seen his son.
在我们的《海底总动员》示例中,马林首先向多莉询问,问“您知道尼莫在哪里吗?” 如果她拒绝,他会问Crush相同的问题,因为Crush在最左边的路径上从Dory降下。 如果卡什(Crush)也拒绝,马林(Marlin)会下到布鲁斯(Bruce),尽管害怕成为鲨鱼小食😰,但他会问他是否见过儿子。

Since Bruce says no, assuring Marlin “fish are friends, not food”, Marlin would need to retrace his steps back up the tree to find the next node he hasn’t asked yet. Moving back up to Crush, he would see that he should ask Darla next. Since all of Crush’s descendants have now been questioned, Marlin would move up to Dory, checking her remaining descendants, and so on. In our example, Marlin would need to check with every single character before finally finding Nemo at the end.
由于Bruce拒绝,请确保Marlin“鱼是朋友,而不是食物”,因此Marlin需要回溯到树上,重新寻找自己尚未询问的下一个节点。 回到Crush,他会看到他接下来应该问Darla。 由于现在已经对Crush的所有后代进行了讯问,因此Marlin会上升到Dory,检查她剩余的后代,依此类推。 在我们的示例中,Marlin需要先检查每个角色,然后才能最终找到Nemo。

Just like breadth-first search, depth-first search also has a time complexity of O(n), but the space complexity can differ. Depth-first search generally takes less memory or space, assuming that you can find the node in question before going through the entire tree. Since every level in a binary search tree tends to double (for a balanced tree at least), if your missing node (Nemo) was located lower in the tree, you could save memory using depth-first search. At worst, the space complexity for both methods will be O(n).
就像广度优先搜索一样,深度优先搜索也具有O(n)的时间复杂度,但是空间复杂度可以不同。 深度优先搜索通常占用较少的内存或空间 ,前提是您可以在遍历整个树之前找到有问题的节点。 由于二叉搜索树中的每个级别都趋于翻倍(至少对于平衡树而言),因此,如果丢失的节点(Nemo)位于树的较低位置,则可以使用深度优先搜索来节省内存。 最糟糕的是,两种方法的空间复杂度均为O(n)。
There is plenty more to learn about binary search trees and how to implement them through code, but hopefully this was a helpful jumping off point. If you have any requests for the next data structure to review, let me know in the comments below!
关于二进制搜索树以及如何通过代码实现它们,还有很多要学习的东西,但是希望这是一个有用的起点。 如果您有任何要求查看下一个数据结构的要求,请在下面的评论中告诉我!
翻译自: https://medium.com/swlh/data-structures-101-what-is-a-binary-search-tree-5514e08cc8f
数据结构二叉排序树建立























 1593
1593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








