初学者开发vs
Difficulty: Beginner* | Easy | Normal | Challenging
难度: 初学者* | 简单 | 普通| 具有挑战性的
This article covers Big O notation from the theory to practical examples in the Swift language including constant, linear and polymorphic time examples (but don’t worry, the code is here too!)
本文介绍了从Big O表示法到Swift语言中的理论到实际示例,包括常量,线性和多态时间示例(但请放心,代码也在这里!)
*This is seen as a beginner topic (first year Computer Science degree fare) but is certainly not easy.
*这被视为一个初学者主题(第一年的计算机科学学位课程),但当然并不容易。
先决条件: (Prerequisites:)
Coding in Swift Playgrounds (guide HERE)
Swift操场上的编码(指南HERE )
You’ll need to know something about Arrays in Swift, Loops and if statements
术语 (Terminology)
Algorithm: A process or set of rules to be followed
算法:要遵循的一个过程或一组规则
Big O Notation: A mathematical notation to describe the limiting behaviour of a function when an argument tends towards infinity
大O表示法:一种数学表示法,用于描述自变量趋于无穷大时函数的极限行为
Space complexity: The quantification of the amount of memory taken by an algorithm to run, as a function of it’s input
空间复杂度:算法运行所需的内存量的量化,取决于其输入
Time complexity: The quantification of the amount of time taken by an algorithm to run, as a function of its input
时间复杂度:算法运行所需时间量的量化,取决于其输入
多种方式做同一件事 (Multiple ways to do the same thing)
We can take a simple example.
我们可以举一个简单的例子。
Adding two numbers (yes, a simple example).
将两个数字相加(是,这是一个简单的示例)。
If we were to add two number there are two approaches to take. In this example we want to add 2 and 1
如果我们将两个数相加,则有两种方法。 在此示例中,我们要添加2和1
In this case it doesn’t matter which order we add the two numbers. That is fine, we can have two algorithms that have identical outputs and are as efficient as each other.
在这种情况下,我们将两个数字相加并不重要。 很好,我们可以有两种算法,它们的输出相同,并且效率相同。
However this is not always true.
但是,并非总是如此。
比较算法 (Comparing algorithms)
We are going to compare time efficiency of algorithms, and therefore we need some consistent way to compare two ways of completing a task.
我们将比较算法的时间效率,因此我们需要一些一致的方法来比较两种完成任务的方法。
Students will often think that they can just measure the execution time of two algorithms and see which completes faster. However, there is a problem with this: Your machine performs many calculations and tasks in the background, which your OS obstruficates. How can you know that you are getting a fair test?
学生通常会认为他们只可以衡量两种算法的执行时间,然后看看哪种算法可以更快地完成。 但是,这有一个问题:您的计算机在后台执行了许多计算和任务,而这却使OS难以处理。 您怎么知道自己正在接受公正的考试?
To put it another way, to get a world record the maximum wind assistance is 2.0 meters per second. It wouldn’t be fair to measure runners under entirely different running conditions — and the same is true for your algorithms.
换句话说,要获得世界纪录,最大的助风能力是每秒2.0米。 在完全不同的运行条件下测量跑步者是不公平的,对您的算法也是如此。
One answer would be, just make the conditions the same for each algorithm and run them then. Yes, this seems like a sensible approach. However setting up this competition would be complex. Even running the competition on different machines would be likely to reveal different results.
一个答案是,仅使每种算法的条件相同,然后运行它们。 是的,这似乎是明智的做法。 但是,设置此竞赛将很复杂。 即使在不同的机器上进行比赛也可能会显示不同的结果。
An alternative comparison can be performed on algorithms, one that classifies algorithms into different performance groups. For algorithms these groups are defined by Big O notation.
可以对算法执行另一种比较,将算法分为不同的性能组。 对于算法,这些组由Big O表示法定义。
Big O looks at the number of comparisons and compares them in orders of magnitude. So (generally speaking) any particular algorithm slots into one of the lines shown in the following graph:
大O会查看比较次数,并按数量级进行比较。 因此,(通常来说)任何特定算法都插入下图所示的行之一:

Big O notation says nothing about the speed of execution, but it does say something about the relative time of execution of different algorithms, basing these calculations on the (computationally expensive) comparisons that are made in the execution of the algorithm.
大O表示法并没有说明执行速度,但确实表示了不同算法的相对执行时间,这些计算都基于算法执行时(比较昂贵)的计算。
This helps us ask questions like, when we double the number of inputs, do we need to double the amount of work that needs to be performed?
这可以帮助我们提出这样的问题,例如,当我们将输入数量加倍时,是否需要将需要执行的工作量加倍?
That seems rather abstract so we need to make some concrete examples of how Big O notation can work in real life, for Swift examples.
这似乎很抽象,所以我们需要举一些具体的例子来说明Swift中的Big O符号在现实生活中如何工作。
But before we go there, let us see the basic hierarchy of Big O notation (if it isn’t clear from the graph):
但是在我们去那里之前,让我们看一下大O表示法的基本层次结构(如果在图中不清楚):
- Constant time O(1): operations only take one unit of time 恒定时间O(1):操作仅占用一个时间单位
- Logarithmic time O(log n): The time the algorithm takes grows less fast than the size of input 对数时间O(log n):算法花费的时间增长得比输入大小快
- Linear time O(n): The time the algorithm takes grows linearly with the size of input 线性时间O(n):算法花费的时间随着输入的大小线性增长
Quadratic time O(n²): The time the algorithm grows proportionally to the size of the input, that is exponentially
二次时间O( n²):算法的时间与输入大小成比例增长,即呈指数增长
Since Big O notation classifies algorithms in terms of running time grows when the input size n grows.
由于大O表示法会根据输入大小n增长时运行时间增长来对算法进行分类。
Where we use Big O notation, we are only interested in which order of magnitude our algorithms fall into; that is we consider O(n + 1) to be of the order O(n), remembering that n is the input size.
在使用Big O表示法的地方,我们只对算法属于哪个数量级感兴趣。 也就是说,考虑到n是输入大小,我们认为O(n + 1)的阶数为O(n)。
We should also be aware that Big O notation usually refers to the worst case complexity. That is, the concrete implementation of the algorithm falls underneath the graph shown above.
我们还应该知道, Big O符号通常是指最坏情况下的复杂性 。 也就是说,该算法的具体实现落在上面显示的图表之下。
大O符号Swift范例 (Big O notation Swift examples)
恒定时间O(1) (Constant time O(1))
Constant time algorithms always run the same — that is constant time — no matter the size of the input.
无论输入大小如何,恒定时间算法始终运行相同的时间(即恒定时间)。
Imagine an array, and we take the first element of that array. No matter how big the array is, it always takes the same amount of time.
想象一个数组,我们采用该array的第一个元素。 不管数组有多大,它总是花费相同的时间。
So here we represent 2 arrays, one with a length of 4 and one with a length of 8. But since we are looking at the first element it doesn’t make any difference — it could be 100000 elements long, but we just look at the first element.
因此,在这里我们表示2个arrays ,一个arrays的长度为4,一个arrays的长度为8。但是,由于我们在看第一个元素,因此没有什么区别-它可能长100000个元素,但我们只看一下第一个元素。
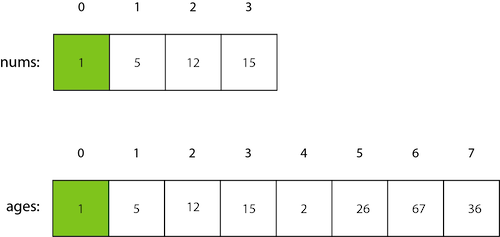
In code?
在代码中?
var nums = [1,2,12,15]
print (nums[0])var ages = [1,2,12,15,2,26,67,36]
print (ages[0])Now as long as the time is constant (for all inputs) we would consider it to be an O(1) algorithm. Different implementations of an algorithm can be faster or slower than one another yet still be O(1) — the reason for this is that the worst case is that the algorithm is O(1) but gives us no more detail than that.
现在,只要时间是恒定的(对于所有输入),我们将其视为O(1)算法。 一种算法的不同实现可能比另一种更快或更慢,但仍然是O(1) ,原因是最坏的情况是该算法是O(1),但没有提供更多细节。
It is worth noting that the execution time of O(1) algorithms does NOT change according to the input size n.
值得注意的是, O(1)算法的执行时间不会根据输入大小n改变 。
对数时间O(log n) (Logarithmic time O(log n))
Binary Search in Swift (the link contains how to test it!) is a divide and conquer algorithm. So the algorithm is O(log n) because while the size of the input is increased, the number of comparisons to find the solution is also increased — but not in a linear fashion.
Swift中的Binary Search (链接包含如何测试!)是一种分而治之的算法。 因此该算法为O(log n),因为当输入的大小增加时,用于查找解决方案的比较次数也会增加—但不是线性的 。
The algorithm takes the middle value of a sorted list, and checks for the target number
该算法采用已排序列表的中间值,并检查目标数字
The following example shows 5 elements, and finds the number 2 in 3 steps.
以下示例显示5个元素,并分3步找到数字2。

The following Swift code is not fast (as it is using ArraySlices), but it is O(log n)
以下Swift代码并不快(因为它使用ArraySlices ),但是它是O(log n)
let target = 2
let sortedArr = [2, 3, 15, 104, 112]
func binarySearch (_ arr: [Int], _ target: Int) -> Bool {
guard arr.count > 0 else {
return false
}
let midPoint = arr.count / 2
if arr[midPoint] == target {
return true
}
if arr[midPoint] > target {
// check lhs
let lhs = arr[0..<midPoint]
return binarySearch(Array(lhs), target)
} else {
// check rhs
let rhs = arr[midPoint + 1..<arr.count]
return binarySearch(Array(rhs), target)
}
}
binarySearch(sortedArr, target)The code above is presented in a gist which should make it reasonably easy to read. See what you think!
上面的代码以要点显示,应该很容易阅读。 看看你的想法!
In any case, Logarithmic time O(log n) does increase the number of comparisons required as the input size increases but the increase is not as fast as the increase in input.
在任何情况下,对数时间为O(log n)的确实增加需要作为输入尺寸的增加比较的次数,但所述增加是不一样快于输入的增加。
That is, it follows a logarithmic increase according to the input size n.
也就是说,它根据输入大小n进行对数增加。
线性时间O(n) (Linear time O(n))
Constant time might be searching through an Array to find an element.
恒定时间可能是在Array搜索以找到元素。
The worst case example of this is rather clear — you might need to search through every element in the array until you find the one you are looking for.
最坏的例子很明显-您可能需要搜索array每个元素,直到找到所需的元素。
var distances = [15,2,104,112,3]
var target = 104
for i in 0..<distances.count {
if distances[i] == target {
print ("found")
}
}In the example above, we needed to search through every element even once we had found our target! This is due to unoptimised code. Let us see the diagram below:
在上面的示例中,即使找到目标,我们也需要搜索每个元素! 这是由于未优化的代码。 让我们看下图:

We can do better! Why not just stop when we’ve found the target?
我们可以做得更好! 找到目标之后,为什么不停下来呢?
It turns out that we can do just that.
事实证明,我们可以做到这一点 。
var distances = [15,2,104,112,3]
var target = 104
for i in 0..<distances.count {
if distances[i] == target {
print ("found")
break
}
}After we have found the element, the break breaks out of the for in loop. That means that we only need to complete three iterations of the loop which makes this algorithm rather more efficient.
找到元素后,中断从for in中断 循环。 这意味着我们只需要完成循环的三个迭代,这会使该算法更加有效。
However, both variations of the algorithm are O(n). This might seem surprising, but this is just the order of magnitude of the algorithm (worst case).
但是,算法的两个变体都是O(n) 。 这似乎令人惊讶,但这只是算法的数量级(最坏的情况)。
That is the worst case of both variations of the algorithms are O(n), so the execution time increases in-step with the input size n.
这是两种算法都为O(n)的最坏情况,因此执行时间随着输入大小n的增加而逐步增加。
二次时间O( n² ) (Quadratic time O(n²))
The worst-case runtime of bubble sort is O(n²) because it has a nested loop. This should be obvious when the you see the code in Swift (if you are unsure how Bubble Sort works check this link!)
冒泡排序的最坏情况运行时间是O(n²),因为它具有嵌套循环。 当您在Swift中看到代码时,这应该很明显( 如果您不确定Bubble Sort的工作方式,请检查此链接 !)
func bubbleSort(_ arr: [Int]) -> [Int] {
guard arr.count > 1 else {return arr}
var sortedArray = arr
for i in 0..<sortedArray.count {
for j in 0..<sortedArray.count-i-1 {
if sortedArray[j]>sortedArray[j + 1] {
sortedArray.swapAt(j + 1, j)
}
}
}
return sortedArray
}Although this particular implementation isn’t the most inefficient (it does cut down a few comparisons during the algorithm) it is still has a worst case time complexity of O(n²) because it is this order or magnitude — that is the nested loop makes the worst case time complexity O(n²).
尽管此特定实现并不是效率最高的(它确实减少了算法中的一些比较),但它仍然具有最差的时间复杂度O(n²),因为它是这个数量级或大小-嵌套循环使得最坏情况下的时间复杂度O(n²)。
指数时间O(2 ^ n) (Exponential time O(2^n))
The first thing to say is exponential algorithms can actually be Ok — if (say) the input is small there may be no particular problem. There may also be no better algorithm that has ever been found for a particular problem, which means that we are stuck with an exponential algorithm that can become unusable for larger n.
首先要说的是指数算法实际上可以-如果输入很小,则可能没有特别的问题。 可能还没有针对特定问题找到更好的算法,这意味着我们陷入了指数算法的困境,对于较大的n而言,它可能变得无法使用。
func fib (_ number: Int) -> Int {
if number <= 1 {return number}
return fib(number - 2) + fib(number - 1)
}This can be called with something like fib(3) . The issue is that to calculate fib(3), we much calculate both fib(2) and fib(1). This doesn’t seem like a large lookup when n in small (in this case 3), but when n increases to say 11 the number of lookups increases…exponentially!
可以使用诸如fib(3)类的东西来调用它。 问题是要计算fib(3),我们需要同时计算fib(2)和fib(1)。 当n较小时(在本例中为3),这看起来好像不是较大的查找,但是当n增加到11时,查找的数量呈指数增长!
It is this exponential growth for time complexity that means that it is increasingly difficult to calculate the result of such an algorithm when n gets larger.
时间复杂度的这种指数增长意味着,当n变大时,越来越难以计算这种算法的结果。
大O记法排序备忘单 (Big O notation sorting cheatsheet)

结论 (Conclusion)
Stop and think about what you’re doing. If you want to make a function, you can use Big O notation to define how fast that particular algorithm that will run in a theoretical sense. After some time O(1), O(n), O(log n), O(n log n) and O(n²) will eventually become second-nature and actually help you think through your algorithm design and how you might make your Apps run better!
停下来想一想你在做什么。 如果要创建函数,可以使用Big O表示法定义该特定算法在理论上可以运行的速度。 一段时间后, O(1) , O(n) , O(log n),O(n log n)和O(n²)最终将变成第二自然,并实际上帮助您思考算法设计以及如何做您的应用程序运行得更好!
翻译自: https://medium.com/swlh/beginners-big-o-for-swift-developers-c1ca94f2520
初学者开发vs





















 407
407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








