quantum_用ai或Quantum解决数独

quantum

人工智能 ， 计算机科学 (Artificial Intelligence, Computer Science)

深入了解之前的一些历史记录： (A little bit of history before diving deeper:)

Photo by John Morgan on Unsplash

John Morgan在 Unsplash上的 照片

“History is called the mother of all subjects”, said Marc Bloch. So, let’s talk about how the famous Sudoku even came into existence. The story dates back to the late 19th Century and it originated from France. Le Siecle, a French daily published a 9x9 puzzle that required arithmetic calculations to solve rather than logic and had double-digit numbers instead of 1-to-9 with similar game properties like Sudoku where the digits across rows, columns, and diagonals if added, will result in the same number. In 1979 a retired architect and puzzler named Howard Garns is believed to be the creator behind the modern Sudoku which was first published by Dell Magazines in the name of Number Place. The puzzle was first published in the name Sudoku in 1986 by a Japanese puzzle company named Nikoli.

“历史被称为所有学科的母亲”，马克·布洛赫(Marc Bloch)说。 因此，让我们谈谈著名的数独是如何诞生的。 这个故事可以追溯到19世纪末，起源于法国。 法国日报Le Siecle发布了一个9x9拼图，该拼图需要算术运算来求解而不是逻辑，并且具有类似两位数的游戏属性(如数独)，其中两位数而不是从1到9 ，将得出相同的数字。 1979年，一位名叫霍华德·加恩斯 ( Howard Garns )的退休建筑师和困惑者被认为是现代数独游戏的创造者，该游戏最初由《 戴尔杂志》以Number Place的名义出版。 1986年，日本一家名为Nikoli的拼图公司以数独的名字首次发布了该拼图。

解决数独问题： (Framing the Problems in solving a Sudoku:)

Sudoku is a real-world example of a Constraint Satisfaction Problem (CSP) as the variable set, domain set and the set of constraints are all finite. We must enter numbers ranging from 1–9 in a 9x9 table in such a manner that the numbers in every row, column, and in every 3x3 sub-table contains each number exactly once. There exists another variation of Sudoku too, which is Diagonal Sudoku with an extra set of constraints stating in each of the table diagonals each number must exactly be featured once. As we know about the constraint satisfaction domain the optimal solution must satisfy all the constraints or more specifically it should abide by the rules of the game. The optimal solution will satisfy all the constraints in the set thus will solve the puzzle.

数独是约束满足问题(CSP)的真实示例，因为变量集，域集和约束集都是有限的。 我们必须在9x9表中输入1–9范围内的数字，以使每一行，每一列和每个3x3子表中的数字恰好包含每个数字一次。 Sudoku也存在另一种变化，即Diagonal Sudoku，它在表对角线的每个对角线中都规定了一组额外的约束，每个数字必须准确地具有一次特征。 我们知道约束满足域，最优解必须满足所有约束，或更具体地说，它应该遵守游戏规则。 最优解将满足集合中的所有约束，从而解决难题。

Computationally the constraints of solving a n x n sudoku can be solved in nondeterministic polynomial time (NP) as the constraints can be solved with some very specific brute-force algorithms and the validity of the set of solutions can be tested in polynomial time too where the inputs to the problem are associated with a set of solutions of polynomial length. A completely solved Sudoku is an example of a Latin Square (n x n array filled with n different symbols, as described by Euler). The Sudoku problem can be thought of as a graph coloring problem where we need to color the graph using only 9 colors and the exposed letters can be thought of as a partial color.

计算上，解决nxn数独的约束可以在不确定的多项式时间(NP)中解决，因为可以使用一些非常特殊的蛮力算法来解决约束，并且解决方案集的有效性也可以在多项式时间内进行检验，其中输入问题的答案与多项式长度的一组解相关。 完全解决的数独就是拉丁方格的示例(如Euler所述，nxn数组填充有n个不同的符号)。 数独问题可以认为是图形着色问题，其中我们仅需要使用9种颜色对图形进行着色，而裸露的字母可以认为是部分颜色。

使用人工智能算法集满足约束： (Satisfying Constraints with Artificially Intelligent set of Algorithms:)

The founding principles of Computational Sciences stand on the ability to satisfy certain constraints with the help of logic. In the scenario of solving sudoku, we must train the solver to look for some specific match-winning patterns besides the basic rules. So, the thing is the system is not just following the rules blindly it is also taking some decisions keeping in mind its near and long-term effects. These patterns are called Heuristics. Similar to expert players who happen to know about some tips and tricks of the game, knowing only the basic rules doesn’t make them an expert in the game. So, while we develop the algorithms and solve our problems we must keep in mind the useful heuristics which we should also include in our program to make it smarter and more useful when it comes to winning.

计算科学的基本原理是依靠逻辑来满足某些约束的能力。 在解决数独问题时，我们必须训练求解器以寻找除基本规则外的一些特定的获胜模式。 因此，问题在于系统不仅在盲目地遵循规则，而且在考虑其近期和长期影响的同时做出一些决策。 这些模式称为启发式 。 与碰巧知道游戏一些技巧的专家玩家类似，仅了解基本规则并不能使他们成为游戏专家。 因此，当我们开发算法并解决问题时，我们必须牢记有用的启发式方法，我们还应将其包含在程序中，以使其在获胜时变得更聪明，更有用。

For our Sudoku Solver, we will take input the sequence of 81 numbers as a string and will represent unsolved numbers with ‘.’(period). To solve the problem we are going to do is replace the ‘.’ with all the probable numbers which can be placed into that cell.

对于Sudoku Solver，我们将输入81个数字的序列作为字符串，并使用'。'(句点)表示未解决的数字。 要解决该问题，我们将替换为“。”。 以及可以放入该单元格的所有可能数字。

According to the constraints of the Sudoku, we cannot use a single digit more than once in a row, column, or in a 3x3 sub-square in the vicinity of any cell. In the case of Diagonal Sudoku, we must also take into consideration the same constraint. We start by replacing the period with all possible numbers from 1 to 9. We do this programmatically by using the following grid_values function.

根据数独的限制，我们不能在任何单元格附近的行，列或3x3子正方形中多次使用一个数字。 在对角数独的情况下，我们还必须考虑相同的约束。 我们首先用所有可能的数字1到9替换句点。我们使用以下grid_values函数以编程方式进行此操作 。

# For the sake of caluclation we take rows as alphaneumeric and columns as numeric. 
rows = 'ABCDEFGHI' 
columns = '123456789'
boxes = [r + c for r in rows for c in columns]  #every possible cell combination in the grid.


def grid_values(grid):
  """
  Take in the Unsolved Sudoku Sequence and replaces the unsolved boxes initially with all
  possible values which can get into that cell. Lastly returns a dictionary containing the 
  values at all cell positions along with cells. 
  """
  values = []
  every_digits = '123456789'
  for n in grid:
    if c == '.':   # replacing every unsolved value with every possible value initially.
      values.append(every_digits)
    else:          # if already solved, causing it no change. 
      values.append(c)
   assert len(values) == 81
   return dict(zip(boxes, values)) #returning the sudoku grid with all possible cell values.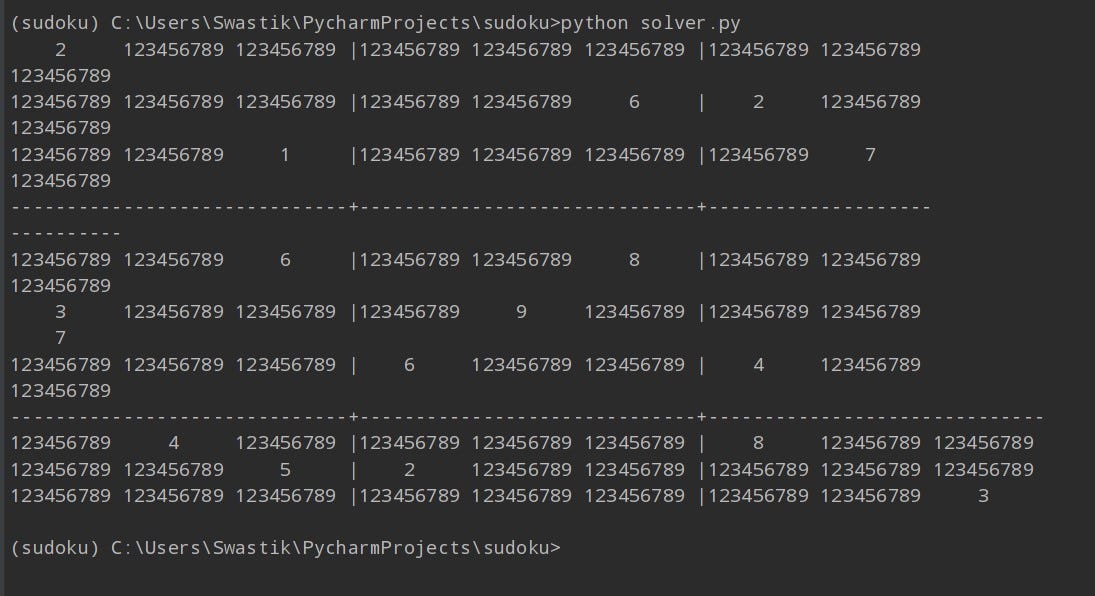

Assigning all possible values initially at all the unsolved cells.

首先在所有未解决的单元格中分配所有可能的值。

As we have now replaced the unsolved cells with all possible numbers from 1 to 9, we know from the basic rules of the Sudoku that we cannot use a number twice if it has already been used across that row, column and within the 3x3 sub-square of that cell. So, let us eliminate them if we encounter them at the unsolved grids which we have filled with all possible numbers initially. So let us take a look at how we can eliminate those irrelevant numbers from the unsolved cells using the eliminate python method.

现在，我们用1到9之间的所有可能数字替换了未解决的单元格，从数独的基本规则中我们知道，如果数字已经在该行，列和3x3子字段中使用过，我们就不能使用它两次。该单元格的平方。 因此，让我们消除它们，如果我们在未解决的网格中遇到它们时，我们最初已经用所有可能的数字填充了它们。 因此，让我们看一下如何使用消除 python方法从未解决的单元中消除那些不相关的数字。

columns_reversed = columns[::-1] #reversing the columns for calculating the Diagonal Units.


def make_combinations(m, n):
  """
  Takes in input of generally iterables and creates all possible combintation out of them.
  args:
   a: string iterable
   b: string iterable
   return : list of all possible combination. 
  """
  return [x + y for x in m for y in n]


row_units = [make_combinations(r, columns) for r in rows]
column_units = [make_combinations(rows, c) for c in columns]
sub_square_units = [make_combinations(m, n) for m in ('ABC', 'DEF', 'GHI') 
                    for n in ('123','456','789')]
diagonal_1_units = [[rows[i]+columns[i] for i in range(len(rows))]]
diagonal_2_units = [[rows[i]+columns_reversed[i] for i in range(len(rows))]]
diagonal_units = diagonal_1_units + diagonal_2_units
all_units = row_units + column_units + square_units + diagonal_units
units = dict((b, [u for u in all_units if b in u]) for b in boxes)
peers = dict((b, set(sum(units[b], [])) - {b}) for b in boxes)


def eliminate(values):
  """
  Eliminate the redundant numbers from the unsolved cells if the number already appeared once 
  in the peer of the current cell. 
  What we do here is we erase that redundant number from the unsolved value cells if appeared once. 
  """
  solved_cells = [box for box in values.keys() if len(values[box]) == 1] # cell is solved if there's only one digit
  for box in solved_cells:
    value_at_cell = values[box]   # retrieve the current value at that cell.
    for peer in peers[box]:       # check for the cell's peers if the value appears again.
      values[peer] = values[peer].replace(value_at_cell, '')
   return values   # return the modified values dictionary.

So, while satisfying these constraints we sometimes come across some cells where only a single digit can be placed, no other digit becomes viable for that specific cell except that digit. We fill in these at the very first of all. With their proper solution. We call this Only Choice, the easiest heuristic to solve a cell of a sudoku grid.

因此，在满足这些约束的同时，有时我们会遇到一些只能放置一个数字的单元格，但除该数字外，其他数字对于该特定单元格都不再可行。 我们首先要填写这些内容。 有了适当的解决方案。 我们称此为Only Choice ，这是解决数独网格单元的最简单的启发式方法。

def only_choice(values):
  """
  If in order to satisfy the constraints of the Sudoku Puzzle there is only a single viable option
  we fill in the Cell with that option only and thereby obtain a solve for the cell. 
  
  """
  for unit in all_units:     #searching across all the vicinity of the cell.
    for digit in '123456789':  
      to_be_filled = [cell for cell in unit if unit in values[unit]]
      if len(to_be_filled) == 1:  # if there exists only a single cell in the unit which is not solved
        values[to_be_filled[0]] = digit  # We fill in the cell with its proper answer.    
  return values

In our journey so far around Constraint Satisfaction, there might come a situation where there will be two unsolved cells in a unit (considering row, column, and 3x3 sub-square) where only two specific remaining numbers can be assigned. So, these two numbers can be effectively removed from the possible numbers on other cells in the same unit. This heuristic is called the Naked Twins. The algorithm implementation specifically makes a deep copy of the grid values and checks for the naked twins' feasibility that is whether there are exactly two unsolved cells which can accept only two specific values and if it does it goes ahead and removes those two values from other cells in the same unit. We implement it programmatically by using the naked_twins function as written below:

在迄今为止围绕约束满足的过程中，可能会出现以下情况：一个单元中将有两个未解决的像元(考虑行，列和3x3子正方形)，其中只能分配两个特定的剩余数。 因此，这两个数字可以有效地从同一单元中其他单元格上的可能数字中删除。 这种启发式方法称为“ 裸双胞胎” 。 该算法的实现专门制作了网格值的深层副本，并检查了裸双胞胎的可行性，即是否存在两个仅能接受两个特定值的未解决单元格，如果可以，它将继续进行并从其他两个网格中删除这两个值同一单元中的单元格。 我们使用如下所示的nude_twins函数以编程方式实现它：

def naked_twins(values):
	"""
	If there are two unsolved cells in a same unit exist such that it can only be filled by only 
	two specific digits, then those two digits can be safely removed from all other cells in the same unit.
	"""
	twins_possible = [unit for unit in values.keys() if len(values[unit]) == 2]  
	twins = [[unit1, unit2] for unit1 in twins_possible for unit2 in peers[unit1] 
					 if set(values[unit1]) == (set(values[unit2]))]    #confimed Naked Twins
	for twin in twins:
		unit1 = twin[0] 
		unit2 = twin[2]
		peers1 = set(peers[unit1])  
		peers2 = set(peers[unit2])
		common_peers = peers1 & peers2  #finding the intersection between the peers of the two naked twin element
		for peer in common_peers:
			if len(values[peer]) >  1:
				for value in values[unit1]:
					values[peer] = values[peer].replace(val, ''))  # Erasing the values. 
	return values

We now try to reduce the puzzle as much as possible by repeatedly applying these three constraint satisfaction algorithms and checking if it is stuck and cannot reduce any further. We do this programmatically by using the reduce_puzzle function. What we do is we call the previous three function inside a for loop and terminate it when the number of solved cells in both the input and the output sequence of the grid values are the same, which means that it cannot be reduced any further by only the constraint satisfaction algorithms alone.

现在，我们尝试通过重复应用这三个约束满足算法并检查它是否卡住并且无法进一步减少，来尽可能地减少难题。 我们通过使用reduce_puzzle函数以编程方式执行此操作。 我们要做的是在for循环中调用前三个函数，并在网格值的输入和输出序列中的已解决单元数相同时终止该函数，这意味着不能再进一步减小它仅约束满足算法。

def reduce_puzzle(values):
	"""
	Applying the 4 Constraint Satisfaction Algorithms until it is not further reducible. 
	Checking if the Number of Solved Cells between the iteration.
	"""
	solved_values = [unit for unit in values.keys() if len(values[unit]) == 1] # considering solved cells
	stuck = False #boolean flag to determine the end of loop
	while not stuck:
		prev_solved_values = len([unit for unit in values.keys() if len(values[unit]) == 1]) #checkpoint 1
		values = eliminate(values) # applying Elimination CSP
		values = only_choice(values) # applying Only Choice CSP
		values = naked_twins(values)  # applying Naked Twins CSP
		after_solved_values = len([unit for unit in values.keys() if len(values[unit]) == 1])
		stuck = after_solved_values == prev_solved_values  # Getting out of loop is the number of solved cell is still the same as the previous iteration.
		
		if len([unit for unit in values.keys() if len(values[unit]) == 0]):
			return False   # if there's problems in the internal representation of the sudoku grid return False. 
	return values			# return the reduced grid values.

If the sudoku grid is still not solved with the constraint satisfaction problem, a partial solution will get to the output where a few of the cells will still be assigned to certain possible values. In these circumstances what we do is we use a search tree to search for the optimal set of digits in those places. We use Depth First Search (DFS) algorithm to traverse through the search tree. So basically with DFS we create up a few instances with the same grid and try out different possible assignments for each of the yet-unsolved cells. We recursively call for the CSP algorithms to reduce the grid based on the search results. We implement it programmatically as below:

如果数独网格仍未通过约束满足问题解决，则部分解决方案将到达输出，其中一些单元格仍将分配给某些可能的值。 在这种情况下，我们要做的是使用搜索树搜索那些位置中的最佳数字集。 我们使用深度优先搜索(DFS)算法遍历搜索树。 因此，基本上，使用DFS，我们用相同的网格创建了几个实例，并为每个尚未解决的单元尝试了不同的可能分配。 我们递归地要求CSP算法根据搜索结果减少网格。 我们以编程方式实现它，如下所示：

def search(values):
	"""
	Recursive Depth-First Search: If the sudoku grid is not further reducible by constraint satisfaction
	a few of the cells will be left with different options and with DFS with search for the optimal 
	values for those yet-unsolved cells.  
	"""
	values = reduce_puzzle(values) # We call the Reduction Function to reduce the puzzle further based on the search results across iterations. 
	if values is False:
		return False
	if all(len(values[b]) == 1 for b in boxes):
		print("Sudoku Problem Solved!")
		return values
	m, n = min((len(values[b]), b) for b in boxes if len(values[b]) > 1)
	for value in values[n]:
		new_sudoku = values.copy()
		new_sudoku[n] = value
		attempted = search(new_sudoku)
		if attempted:
			return attempted

We use the display sudoku function to display the input string sequence as a two-dimensional 9x9 Sudoku grid:

我们使用display sudoku函数将输入的字符串序列显示为二维9x9 Sudoku网格：

def display(values):
    """
    Display the values as a 2-D grid.
    Input: The sudoku in dictionary form
    """
    width = 1 + max(len(values[b]) for b in boxes)
    line = '+'.join(['-' * (width * 3)] * 3)
    for r in rows:
        print(''.join(values[r + c].center(width) + ('|' if c in '36' else '')
                      for c in cols))
        if r in 'CF':
            print(line)
    return

To solve a Sudoku Sequence we call the above functions like the following:

为了解决数独序列，我们将上述函数调用如下：

if __name__ == "__main__":
    diag_sudoku_grid = '2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3'
    values = grid_values(diag_sudoku_grid)
    values = reduce_puzzle(values)
    values = search(values)
    display(values)

The output looks like the following, where the set of algorithms have been successful in calculating the answer.

输出如下所示，其中一组算法已成功计算出答案。

Completely Solved Diagonal Sudoku.

完全解决了对角数独问题。

解决数独作为约束满足问题的量子方法： (The Quantum Approach to Solving Sudoku as a Constraint Satisfaction Problem:)

We will now try to solve a simple Sudoku Grid with Quantum Simulated Annealing. First things first, what is the simulated annealing? The idea is for optimization problems like this we use some sub-optimal heuristics and obtain the optimal set of heuristics to obtain the optimal solution. We have used here the DWave AQC Model (Adiabetic Quantum Computing) to sample out the optimal solution which satisfies the constraints discussed earlier.

现在，我们将尝试使用“量子模拟退火”解决简单的Sudoku网格。 首先，什么是模拟退火？ 对于这样的优化问题，我们的想法是使用一些次优启发式算法，并获得最优的启发式算法集以获得最优解。 我们在这里使用DWave AQC模型(糖尿病量子计算)来采样满足前面讨论的约束的最佳解决方案。

使用DWave Kerberos混合采样器： (Using the DWave Kerberos Hybrid Sampler:)

We are in this example working with the hybrid solver provided with DWave. It finds out the optimal set of heuristics by running a parallel tabu search. It’s a hybrid solver as it uses both quantum and the classical properties of computation underneath. It is also a decomposition sampler that uses an asynchronous workflow while processing. It’s included in the Ocean SDK package of the DWave Systems. To get started with the development locally make sure you have Python 3.5+ installed on your system and issue the following command.

在本示例中，我们正在使用DWave随附的混合求解器。 它通过运行并行禁忌搜索来找出最佳的启发式方法。 它是一种混合求解器，因为它同时使用了量子计算和经典的计算特性。 它也是一个分解采样器，在处理时使用异步工作流。 它包含在DWave Systems的Ocean SDK软件包中。 要开始本地开发，请确保您的系统上安装了Python 3.5+，然后发出以下命令。

python -m pip install --upgrade pippip install dwave-ocean-sdk

使用二进制二次模型(BQM)进行计算： (Using Binary Quadratic Models (BQM) for the calculations:)

We cannot frame the constraints directly ready to be fed to the Quantum Computers, we need an intermediate representation for it to be getting fed. That’s why we will use BQM, fortunately, DWave Ocean SDK already provides a tool called combinations which can be used to frame Constraint Satisfaction Problems into BQMs. Firstly Binary Quadratic Models as the name itself suggests is a system of the equation which is quadratic and is expressed in Binary. Due to higher complexities in calculations, Quantum computers use these to significantly speed up the development process. So, back in the game we were we have decided to use the combinations tool from dimod which is going to return a Binary Quadratic Model which is minimized for each of the k-combinations of its input and internal variables.

我们无法构造直接准备将其馈送到Quantum Computers的约束，我们需要一个中间表示来将其馈入。 这就是为什么我们将使用BQM的原因，幸运的是，DWave Ocean SDK已经提供了一个称为“ 组合”的工具，该工具可用于将约束满足问题归结为BQM。 首先，顾名思义，二进制二次模型本身就是一个方程系统，它是二次的，用二进制表示。 由于计算的复杂性更高，Quantum计算机使用这些计算可以大大加快开发过程。 因此，在游戏中，我们决定使用dimod的组合工具，该工具将返回一个二进制二次模型，该模型对于其输入变量和内部变量的k个组合中的每一个均最小。

We start by importing necessary packages from the dwave-ocean-sdk and do some sanity check before actually reading into the Sudoku Grid.

我们首先从dwave-ocean-sdk导入必要的软件包，并在实际读入Sudoku Grid之前进行一些完整性检查。

import dimod  
import math 
import sys
import dimod.generators.constraints import combinations
from hybrid.reference import KerberosSampler


def prettify(row, col, digit):
    return "{row}, {col}_{digit}".format(row, col, digit)


def read_matrix(filename):
    with open(filename, 'r') as f:
        all_lines = f.read()
    lines = []
    for line in all_lines:
        new_line = line.rstrip()
        if new_line:
            new_line = list(map(int, new_line.split(' ')))
            lines.append(new_line)
    return lines 




def sanity_check(matrix):
    n = len(matrix)
    m = int(math.sqrt(n))
    unique_digits = set(range(1, 1+n))


    for row in matrix:
        if set(row) != unique_digits:
            print("Error in row", row)
            return false
    for j in range(n):
        col = [matrix[i][j] for i in range(n)]
        if set(col) != unique_digits:
            print("Error in column", col)


    subsquare_idx = [(i, j) for i in range(m) for j in range(m)]
    for r_scalar in range(m):
        for c_scalar in range(m):
            subsquare = [matrix[i + r_scalar * m ][j + c_scalar * m] for i, j in subsquare_idx]
            if set(subsquare) != unique_digits:
                print('Error in sub-square', subsquare)
                return True


    return True

We now go ahead and create up the Binary Quadratic Models using combinations tools from all the available variable combinations of the Sudoku Grid’s rows, columns, and sub-square indices.

现在，我们使用Sudoku Grid的行，列和子平方索引的所有可用变量组合，使用组合工具来创建二进制二次模型。

def main():


    if len(sys.argv) > 1:
        filename = sys.argv[1]
        
    matrix = read_matrix(filename)
    n = len(matrix)
    m = int(math.sqrt(n))
    digits = range(1, n+1)


    bqm = dimod.BinaryQuadraticModel({}, {}, 0.0, dimod.SPIN)


    for row in range(n):
        for col in range(n):
            node_digits = [prettify(row, col, digit) for digit in digits]
            one_digit_bqm = combinations(node_digits, 1)
            bqm.update(one_digit_bqm)


    for row in range(n):
        for digit in digits:
            row_nodes = [prettify(row, col, digit) for col in range(n)]
            row_bqm = combinations(row_nodes, 1)
            bqm.update(row_bqm)
    for col in range(n):
        for digit in digits:
            col_nodes = [prettify(row, col, digit) for row in range(n)]
            col_bqm = combinations(col_nodes, 1)
            bqm.update(col_bqm)




if __name__ == "__main__":
    main()

So, that is it. We have successfully implemented two intelligent solutions one of which uses classical Computation and uses Artificially Intelligent Heuristic, really powerful, and can solve even diagonal sudoku grids. The second one uses an Asynchronous hybrid heuristic sampler which also happens to use state of the art Simulated Annealing of the Adiabatic Quantum Computing model to perform a conversion of the Constraint satisfaction problem to a Binary Quadratic Model to perform sampling over it and thereby obtaining the optimal solution.

就是这样。 我们已经成功实现了两种智能解决方案，其中一种使用经典计算，并且使用了功能非常强大的人工智能启发式算法，甚至可以解决对角数独网格。 第二种使用异步混合启发式采样器，该采样器也恰好使用绝热量子计算模型的模拟退火来将约束满足问题转换为二进制二次模型以对其进行采样，从而获得最佳采样解。

I am earnestly grateful to you for your time.

我衷心感谢您的光临。

“Even the greatest fool can accomplish a task if it were after his or her heart. But the intelligent ones are those who can convert every work into one that suits their taste.” — Swami Vivekananda.

“即使是最大的傻瓜，只要在他或她的心底下，都能完成任务。 但是聪明的人是那些可以将每件作品转换成适合自己口味的作品的人。” — Swami Vivekananda。

翻译自: https://medium.com/towards-artificial-intelligence/solving-sudoku-with-ai-or-quantum-3421f5af7b54

quantum