python svm 决策方程_从零开始SVM算法(2)-SVM方程推导

上一章我们介绍了SVM算法的意义，SVM是large-margin算法，旨在找到一条能够完全区分训练集而且拥有最大margin值的直线。在这一章节里，我们将推导margin的计算方式和SVM最终要解决的问题的方程表达式。
任意点到决策边界距离（1） － 初步表达式
上章节我们提到，margin值就是所有数据点到决策边界的距离里面的最小值，所以首先我们要计算平面内任意一点到决策边界的距离。为了使得表述和理解更简单，在下面的所有推导中，我们都采用二维平面内的数据作为例子去做解释。二维平面得到的结论可以推广到任意维度的空间当中。

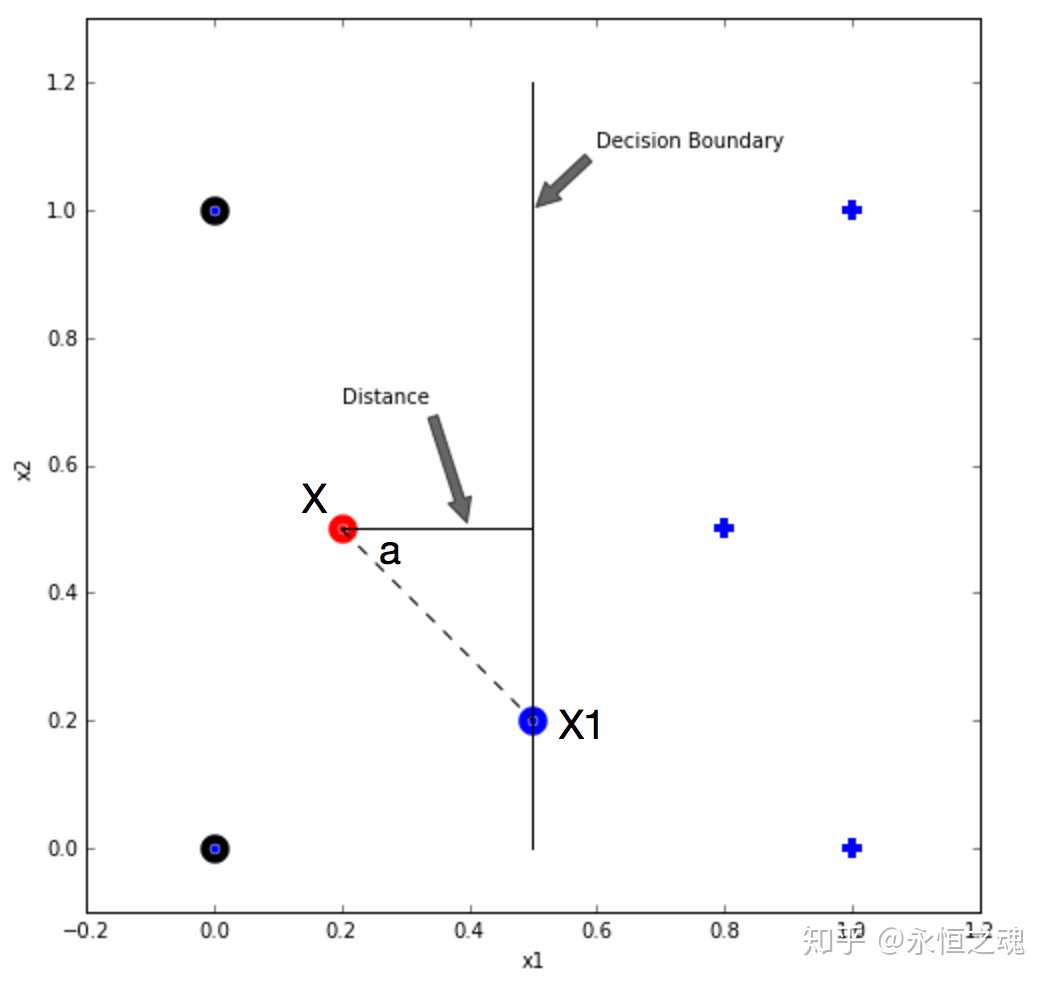
上图是一个在上一章节用过的二维数据集例子。在图中，红色的数据点是需要计算到决策边界距离的点，我们标注其为X。X1为决策边界上的点。注意，这里的X1跟坐标轴上的x1不一样，这里的X1是一个点，也是一个拥有两个维度的向量。坐标轴上的x1是两个维度对应的值的大小，是标量。图中的distance是我们需要计算的距离，该线段与决策边界垂直且与点X相交。
现在，假定图中的决策边界是由特征权重向量W和偏差值b决定的，既对于任意数据点，h(X) = sign(WTX + b)，该分类器是一个线性分类器(linear classifier)。对于任意数据X，当WTX + b > 0的时候预测该点为正类，当WTX + b < 0的时候预测该点为负类。当WTX + b = 0的时候，该点正好落在决策边缘上，此时分类器将其预测为正类来打破平衡(tie-break)。因此，我们很容易得到决策边界的方程为WTX + b = 0。
为了计算点X到决策边界的距离，我们做了一条辅助线，这条辅助线穿过点X和决策边界上的一点X1。根据高中几何知识我们知道X到决策边缘的距离D，是向量X X1长度在垂直于决策边界方向上的投影，既Distance = ||X - X1||cos(a)，a为向量XX1与垂直于决策边界方向的夹角。
此时，要计算Distance大小我们有两个方法，第一个方法是计算角度a以及||X - X1||的大小，第二个方法是找到一个垂直于决策边界的向量，假设是P。则距离

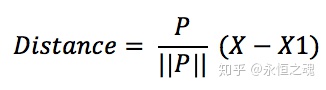
对于以上的公式推导，我们将会在下面演示。
根据经验而言，求法向量P往往比求角度a要简单一些，所以我们在这里采用第二种方法。由于我们最终需要用权重向量W和偏差b来表示距离大小，所以上面公式的是距离的初步表达式，我们还需要进行进一步推算。
任意点到决策边界距离（2） － 初步表达式的证明
刚刚我们提到了第二种计算距离的方法，并给出了计算公式，现在我们要证明计算公式的正确性。
首先根据向量相乘公式我们知道，两个向量相乘等于向量长度的乘积再与向量夹角余弦值的乘积。既