瑞利分布概率密度函数推导_常用概率分布总结(1)

老是记不住各种分布及其意义，每次用时，回查各个课本资料也很麻烦，一些分布的重要性质也是各处散布，经常找不到，故这里做个总结，当作个资料卡用。

内容有各种常见概率分布，一般会写含义、密度函数形式、期望、方差、特征函数，其它性质感觉重要就添加（有趣但感觉没什么用的不会添加）。

先介绍下在R中的使用随机数，密度函数，分布函数，分位函数的命令，使用正态分布为示例。以下不做说明均是使用 R 语言。

• 随机数

从服从某种分布的总体中抽出样本

> rnorm(5)
[1]  0.2858567 -0.7578348  0.6322224  0.6289619 -0.6743083

• 概率密度函数(probability density function pdf)

分布的概率密度函数值

。有时直接称密度函数。

> dnorm(0)
[1] 0.3989423
> dnorm(3.2)
[1] 0.002384088

使用这个函数就可以画出概率密度函数图，

x = seq(-5,5,by=0.01)
y = dnorm(x)
plot(x,y)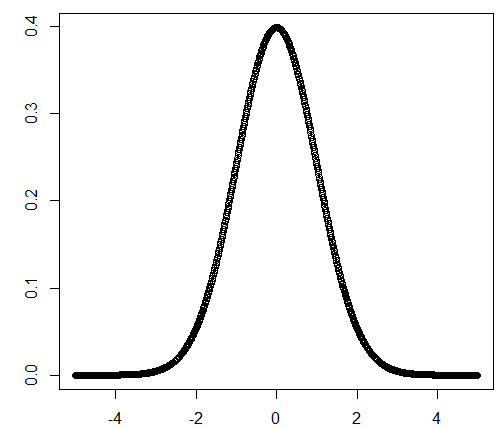

• 累积分布函数(cumulative distribution function cdf)

含义为对pdf的积分函数

。有时直接称分布函数。

> pnorm(0)
[1] 0.5
> pnorm(1.3)
[1] 0.9031995
> pnorm(3.6)
[1] 0.9998409

• 分位函数

cdf的反函数，从pdf理解更简单，pdf下方总的面积为1，q(0.9)表示从

到值q(0.9)处，累积概率为0.9。显然这个函数一个用处是计算否定域

> qnorm(0.5)
[1] 0
> qnorm(0.9031)
[1] 1.29942

> qnorm(0.025)    #显著性水平为0.05，拒绝域(-1.95,1.95)
[1] -1.959964

用随机数理解，如果随机抽取，90%的数在

到值q(0.9)之间，

> qnorm(0.9)
[1] 1.281552

> sum(rnorm(1e5)<1.281552)/1e5
[1] 0.90048

1.退化分布；2.伯努利分布；3.Categorical 分布；4.二项分布；5.多项分布；6.中餐馆分布

7.泊松分布；8.几何分布；9.超几何分布；10.负二项分布（又称巴斯卡分布)；11.正态分布；

12.均匀分布；13.指数分布；14.卡方分布；15.t分布；16.F分布；17.柯西分布；

18.Gamma分布；19.beta分布；20.对数正态分布；21.Weibull分布；22.逻辑分布；23.狄利克雷分布；

1.退化分布(degenerate distribution)

[1]基本

• 密度函数

随机变量值只取常数

。事实上它并不随机，但把它看作随机变量的退化情况，因此称为退化分布。

• 期望

• 方差

• 特征函数

[2]重要性质

2.伯努利分布

[1]基本

随机变量只取0或1，表示事件不发生或发生，也可以说是事件发生0次或发生1次

• 密度函数

为随机变量，

为该分布的参数。

• 期望

• 方差

• 特征函数

[2]重要性质

3.Categorical分布

[1]基本

伯努利分布为一次只有两种可能结果{0,1}的试验，Categorical 分布可以有多种可能{1,2,...,K}。

• 密度函数

• 期望

• 方差

• 特征函数

[2]重要性质

4.二项分布

[1]基本

也称为

重伯努利分布，某伯努利事件成功的概率为

，重复进行

次伯努利事件，成功的次数为

的概率。随机变量为

，可取

• 密度函数

画个密度图看看，

k = 0:15      #随机变量
p = dbinom(k,15,0.7)   #15重伯努利，成功概率取0.7
plot(k,p)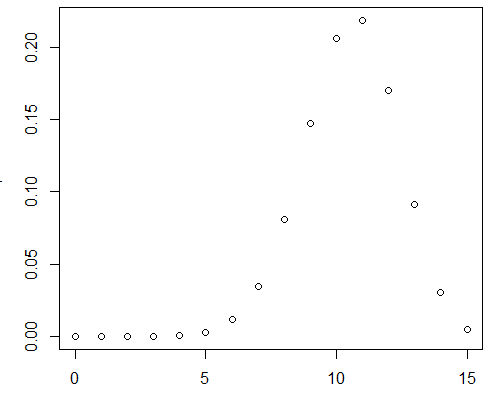

• 期望

• 方差

• 特征函数

[2]重要性质

1.几个二项式系数的关系式

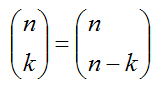
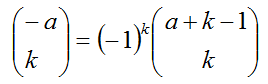
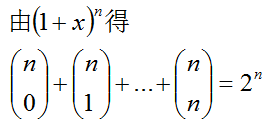
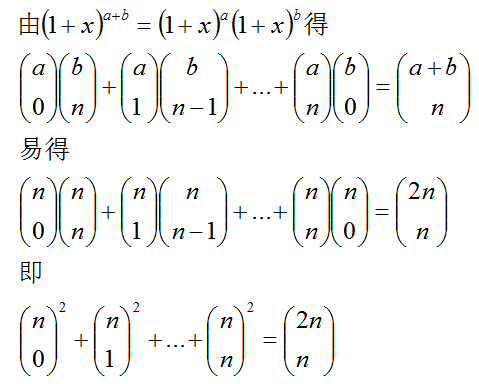
2.二项分在

时近似为正态分布

k = 0:100     
p = dbinom(k,100,0.4)   
plot(k,p)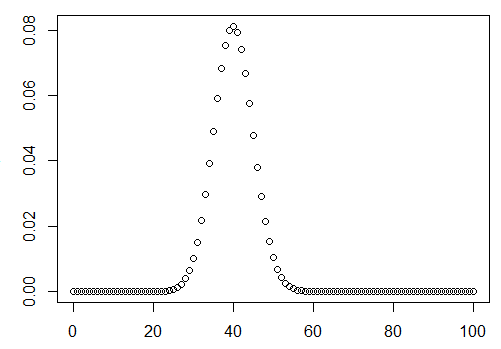

5.多项分布(Multinomial Distribution)

[1]基本

也可以进行多次Categorical 分布试验，Categorical 分布的事件用

表示，对应的概率为

，进行

次试验（每次都会发生

中的一个）各个事件发生的次数为

，注意有

，概率为，

• 密度函数

• 期望

• 方差

• 特征函数

[2]重要性质

1.从离散分布抽iid的样本，样本发生的概率都可以看作是多项分布。多项分布在推导皮尔逊卡方定理、列联表的卡方检验都有用到。是一个重要且很有用的分布。

6.中餐馆分布（Chinese restaurant process CRP ）

这是本专栏中“狄利克雷过程和中餐馆过程”的部分内容，里面同时也说明了该分布的用处。

多次伯努利分布（每次试验只有两种结果）得到二项分布，多次Categorical 分布（每次试验有K种结果）得到多项分布。进一步考虑。如果每次试验有无穷种可能结果，进行多次试验又会如何。

[1]基本

把过程想象成客人进入餐馆就坐的过程，餐馆中有无穷个桌子。每一次试验相当于一个客人选择一个桌子坐下。

圆圈表示餐桌，数字表示客人，1号客人选择了第一个餐桌，4号客人选择了第3个餐桌。

看看上图发生的概率，

首先所有桌都没人，1号进入直接坐在1桌；

2号进入，分别以概率

坐在1桌和一个新的空桌，结果是坐在了1桌；

3号进入，分别以概率

坐在1桌和一个新空桌，结果坐在了一个新空桌2桌；

...

8号进入，分别以概率

分别为进入第1,2,3,4个桌和一个新空桌的概率，结果坐在了3桌；

故上图发生的概率为，

• 概率密度函数

关于这个概率的计算前人早就算好了，

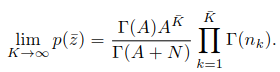
A是

，

为第

类的数量，即坐在第k个桌的人数，

当前非空的桌数量。

library(nimble)

> rCRP(n=1, conc = 2, size=15)     #alpha也称concentration，即这里的conc参数。15个客人
 [1] 1 2 3 1 1 4 5 1 5 1 3 4 1 1 1
> rCRP(n=1, conc = 2, size=15)    #该函数目前只能一次产生一个随机样本，即 n 只能为1
 [1] 1 2 2 2 3 4 3 2 2 3 2 5 5 3 6
> rCRP(n=1, conc = 2, size=15) 
 [1] 1 2 1 3 1 4 4 2 4 4 2 4 1 4 4
> rCRP(n=1, conc = 2, size=15)
 [1] 1 2 1 2 2 1 1 1 1 1 1 1 1 2 1
#可以看到有时分为5类，有时分为6类，有时分为4类，...

z = c(1,1,2,3,1,3,4,3)
dCRP(z, conc = 1, size=8)  #这里看看上面例子发生的概率。注意size要和z的长度值相等
[1] 9.920635e-05

从上面的分析可知

越大，客人坐到空桌的概率越大

，也就

参数越大，上面产生随机样本时类越多。

如果已知c(1,1,2,3,1,3,4)，看上面可以算出

条件概率分布，懒得自己编程，也可以利用dCRP()函数和关系

计算，

a = c()

for(i in 1:5){
  
  z7 = c(1,1,2,3,1,3,4)
  z8 = c(1,1,2,3,1,3,4,i)
  a = c(a,dCRP(z8, conc = 1, size=8)/dCRP(z7, conc = 1, size=7))
}

> a    #即已知前7个情况，第8个客人选择各个餐桌的概率
[1] 0.375 0.125 0.250 0.125 0.125

这里有一个问题是dCRP()可能会很小，看上面size=8时会计算出9.920635e-05，如果size更大概率会更小使得R语言认为该值为0，导致除法没法算，方法自然是计算时使用概率的对数值，dCRP()设置参数log即可，

> dCRP(z1, conc = 1, size=400)   #z1的size=400，即试验了400次
[1] 0

> dCRP(z1, conc = 1, size=i,log=1)  #实际计算时，应该注意这个值为概率对数值
[1] -922.6469

其实可以看到R语言里面很多计算概率的函数都会设置log这个参数，也是预防这个问题。

• 期望

• 方差

• 特征函数

[2]重要性质

7.泊松分布(

)

[1]基本

泊松分布起初是作为二项分布的近似引出的。当二项分布中

很大（计算

困难），而

很小时，取

，有

，其中

。

• 密度函数

为随机变量，可取0, 1, 2, ...

密度图，

k = 0:20    #随机变量取值，可取到无穷大，这里只取到20
p = dpois(k,0.8)
plot(k,p)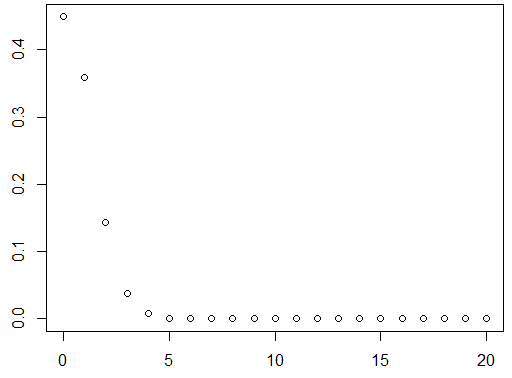

• 期望

• 方差

• 特征函数

[2]重要性质

1.这个分布的期望方差相等

2.极限分布(

)为正态分布

画个 图看看，

k = 0:50
p = dpois(k,20)  #lambda = 20
plot(k,p)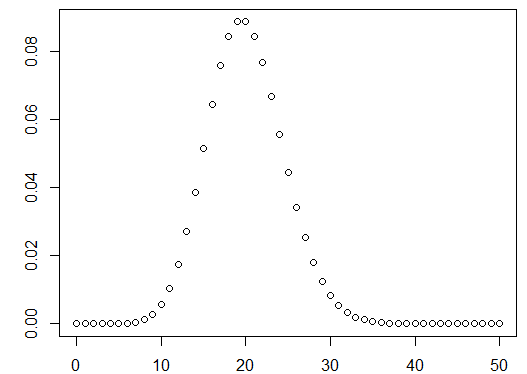

[3]为何要引入泊松分布来近似二项分布

[4]泊松分布也可以不由二项分布推出来，而由一些条件独立于二项分布推出来

[5]广义泊松分布

泊松分布的期望和方差值相等是一个特点，也是一个很强的限制，然而现实生活中大多数据是不符合期望方差相等的，于是创建一个不限制期望方差相等的离散分布。

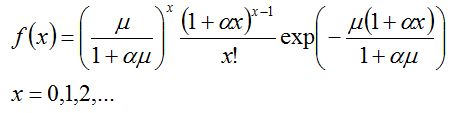
对应期望方差，

时就回到了一般的泊松分布。

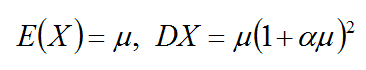
8.几何分布

[1]基本

进行多次伯努利试验，直到第

​次才首次成功的概率，​

为随机变量可取1，2，...

• 密度函数

概率密度图，

k = 0:50      #注意，随机变量确实应该从1开始，但R语言中k=0，实际是+1后再代入计算
p = dgeom(k,0.3)  #在使用rgeom()产生的随机数也是从0开始，应+1
plot(k,p)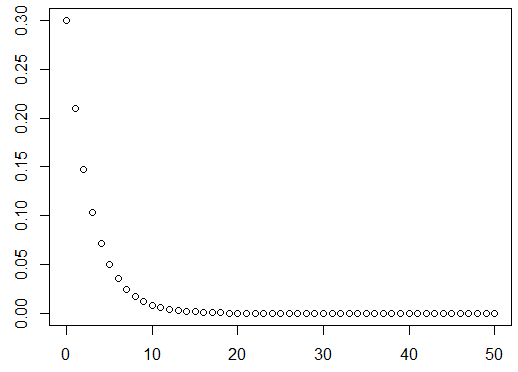

• 期望

• 方差

• 特征函数

[2]重要性质

1.无记忆性

​表示首次成功时的已经试验的次数。一种情况是第​

次首次成功，概率为

；另一种情况，前​次

没有成功，那么再试验​

次首次成功的概率为

。再试验​

次和直接试验​

次概率相同，好像前​

次没有发生，称为无记忆性。只有几何分布有这种无记忆性。

9.超几何分布

[1]基本

一批产品共有

个，次品共有

个，从中抽取

个，则次品

为个的概率。然而，一般是无法提前知道一批产品中共有多少次品。

• 密度函数

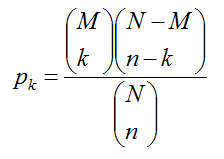
随机变量为

，可取0, 1, 2, ...,

密度图，

k1 = 0:8
p = dhyper(k1,m=10,n=30,k=8)  #产品中次品10个，好品30个，每次抽8个
plot(k1,p)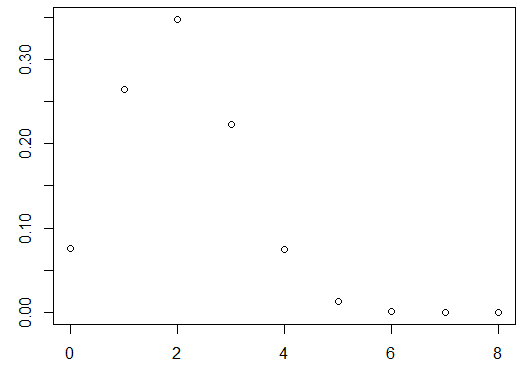

• 期望

• 方差

• 特征函数

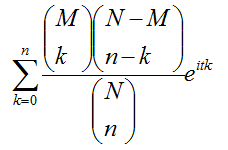
[2]重要性质

10.负二项分布（又称巴斯卡分布)

[1]基本

多重伯努利事件中，已知成功​

次，则达成成功​

次时的试验次数为

​的概率，第​

次试验刚好达到第​

次成功。随机变量为试验次数

​。如，要成功3次，进行5次试验就出现第3次成功的概率

• 密度函数

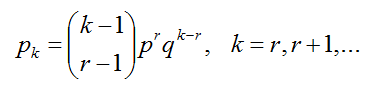
k1 = 0:10   #计算时，会自动 k1+4 ，于是随机变量取值为，4,5,...,14
p = dnbinom(k1,size=4,prob=0.3)  #伯努利试验成功的概率为0.3，需要成功4次
plot(k1,p)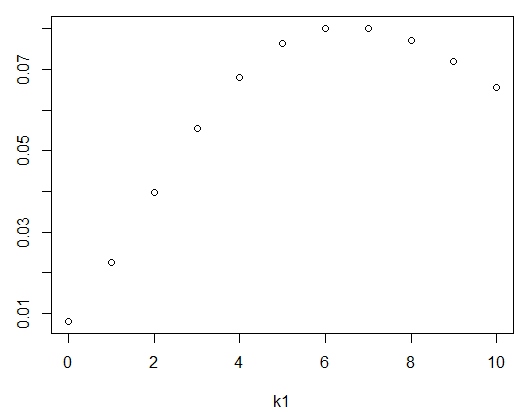

• 期望

• 方差

• 特征函数

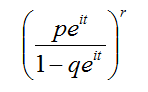
[2]重要性质

1.期望方差的计算：

巴斯卡分布

是重复独立试验（成功概率

）中成功

次所需要的试验次数 可以把它分解为

，其中

为在前一次成功后，再成功一次所需要的试验次数，

服从几何分布,期望为

，方差是

。得，

“ 常用概率分布总结(2)”接其它分布。