
1、真分数、假、带分数。

2、分数的基本性质:
分数的分子分母都乘以或都除以相同的数(零除外),分数的大小不变。
当我们熟练地掌握了这些基本概念后,就应利用它解决实际问题。
1可以化成任何分子分母相同的假分数。
例1、把下面的假分数化成带分数或整数。
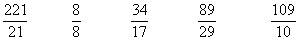
解:
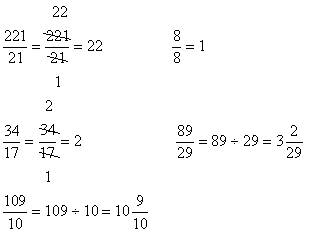
例2、填空:
(1)
(2)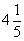 的分数单位是( ),
的分数单位是( ),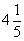 里面有( )个
里面有( )个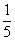 。
。
3里面有( )个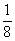 ,有( )个
,有( )个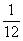 。
。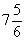 里面有( )个1( )个
里面有( )个1( )个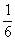 。
。
(3)写出一个比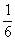 大而比
大而比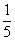 小的分数。
小的分数。
分析解答:
(1)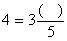 ,将4里拿出一个“1”,写成分母是5的假分数,为整数部分是3,分数部分是
,将4里拿出一个“1”,写成分母是5的假分数,为整数部分是3,分数部分是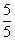 ,则
,则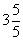 。
。
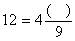 ,
,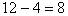 将8化成分母是9的假分数:
将8化成分母是9的假分数: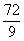 。
。
因为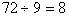 ,所以
,所以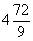 。
。
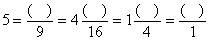
将5化成分母是9的假分数为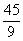 ,化成
,化成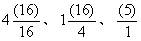 。
。
(2)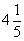 的分数单位是(
的分数单位是(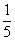 ),它有(21)个
),它有(21)个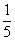 。
。
3里面有(24)个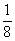 ,因为
,因为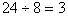 。
。
有(36)个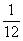 ,
,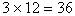 个,因为
个,因为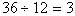 。
。
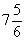 里面有(7)个1(5)个
里面有(7)个1(5)个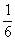 。
。
(3)找出一个比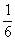 大比
大比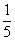 小的分数。
小的分数。
只要把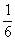 和
和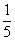 的分子、分母分别相加,就是所求
的分子、分母分别相加,就是所求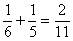 ,
,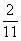 就比
就比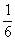 大,比
大,比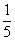 小。
小。
这是什么定理呢?
因为两个不等的分数,如果我们把它们的分子,分母分别相加得到的新分数叫做它们的加成分数,加成分数的值总是在它们的两个分母数之间,根据这个道理你可以写出几百个这样的分数,也不难,只要反复求加成分数就行了。如: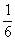 和
和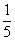 。
。

二法:用扩倍法也能找到比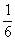 大比
大比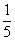 小的数若干个。
小的数若干个。
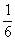 和
和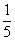
(1)找出它们的最小公倍数:30,则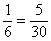 ,
,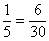 ,
, 和
和 中的比若再扩大2倍,则
中的比若再扩大2倍,则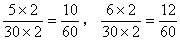 ,这样
,这样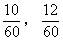 中间就出现了
中间就出现了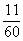 ,还可以扩倍:
,还可以扩倍: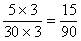 ,
,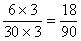 。这样中间,就出现了
。这样中间,就出现了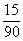 和
和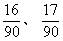 。
。
这些数排队的话为: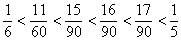 。
。
例3、某分数的分母加上2,分子减去2,所得新分数分母分子的差为123,约分后得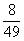 ,求原分数。
,求原分数。
分析:所得新分数分子、分母的差为123,这个新分数约分后是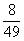 ,那么分子与分母的差应是
,那么分子与分母的差应是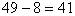 ,我们用数量差÷倍数差得到1倍的数为:
,我们用数量差÷倍数差得到1倍的数为: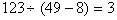 ,这个3就是原分数的分子。
,这个3就是原分数的分子。
那么新约分后的分数要还原回去应是: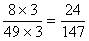
原题分母加上2,分子减去2,我们用逆推法求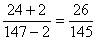 ,则这个原分数为
,则这个原分数为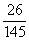 。
。
例4、一个分数分子、分母的和是92,如果分子、分母都减去16,得到的分数化简后是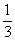 ,求原来的分数。
,求原来的分数。
分析:分子分母之和是92,它们都减去16,说明要减去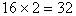 ,则还剩
,则还剩 ,这个60是新分数分子分母之和,这个新分数化简后是
,这个60是新分数分子分母之和,这个新分数化简后是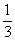 ,说明分子占1份,分母占3份,共有
,说明分子占1份,分母占3份,共有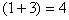 份。用数量和÷份数和,得到
份。用数量和÷份数和,得到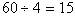 ,则分子为15,分母为45,这时再想还原回去,它们分别减去了16,还要还回来。
,则分子为15,分母为45,这时再想还原回去,它们分别减去了16,还要还回来。
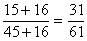
例5、一个最简分数,把它的分子扩大4倍,分母缩小3倍后,可化成10,这个最简分数是多少?
分析:一个分数分子扩大4倍,这个分数值就扩大了4倍。
分母缩小3倍,这个分数值反而扩大3倍。
例如, 分子扩大4倍,则
分子扩大4倍,则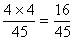 分数值扩大4倍。
分数值扩大4倍。
如分母缩小3倍,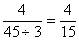 ,说明分数值反而扩大3倍。
,说明分数值反而扩大3倍。
这样这个分数就扩大了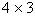 倍,结果是10,我们把10缩小12倍就得到了原来的分数值
倍,结果是10,我们把10缩小12倍就得到了原来的分数值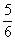 。
。





 公众号推送机制修改之后,很多粉丝留言收不到推送,在这里苗苗老师恳切地呼吁大家:
公众号推送机制修改之后,很多粉丝留言收不到推送,在这里苗苗老师恳切地呼吁大家:
 如果你希望继续可以正常地收到我们的新文章,可以在看完文章后,顺手点一下右下角的蓝色
【在看】, 这样我们又可以每天准时见面了哦。
如果你希望继续可以正常地收到我们的新文章,可以在看完文章后,顺手点一下右下角的蓝色
【在看】, 这样我们又可以每天准时见面了哦。
 另外,时间允许的话,还可以选择
留言,哪怕一个标点符号都可以,这样又可以让系统判断我们的关系更加亲密了。 感谢大家一直以来的关注和支持现在开始,点个“在看”只要你想看,我们都在
- End -
本文来源于
网络,版
权归原作者所有,我们尊重原创,若有侵权请联系删除。责编:苗苗老师。
另外,时间允许的话,还可以选择
留言,哪怕一个标点符号都可以,这样又可以让系统判断我们的关系更加亲密了。 感谢大家一直以来的关注和支持现在开始,点个“在看”只要你想看,我们都在
- End -
本文来源于
网络,版
权归原作者所有,我们尊重原创,若有侵权请联系删除。责编:苗苗老师。


























 917
917

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








