的garch预测_隐含波动率能够作为未来波动率预测吗？

最新推荐文章于 2023-10-16 16:05:54 发布

Huawei_Germany

最新推荐文章于 2023-10-16 16:05:54 发布

阅读量1.5k

点赞数

文章标签：的garch预测

本文链接：https://blog.csdn.net/weixin_29449593/article/details/112660699

版权

本文探讨了隐含波动率作为未来波动率预测的适用性。通过对比传统Black-Scholse公式与无模型隐含波动率方法，指出两者在计算和应用中的优缺点。研究发现，尽管隐含波动率在短期内呈现领先性，但从长期和预测角度来看，其并不能有效预测未来波动率，且与历史波动率相比，预测效果有限。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

隐含波动率能够作为未来波动率预测吗？关于这个问题，点掌小编整理一份资料给到大家。

一、两种隐含波动率

　　隐含波动率是利用期权反推出来的波动率。期权的价值分为内在价值和时间价值，而时间价值主要就是波动价值(其次是纯粹的时间价值，即资金利率价值)。

　　使用期权的价格计算隐含波动率的方法主要有两种，一种是使用传统的Black-Scholse公式将期权价格反推出其中的波动率。另一种是Britten-Jones和Neuberger(2000)首次提出的无模型方法，其理念是将期权的时间价值加权求和，其公式为(左侧即为波动率)：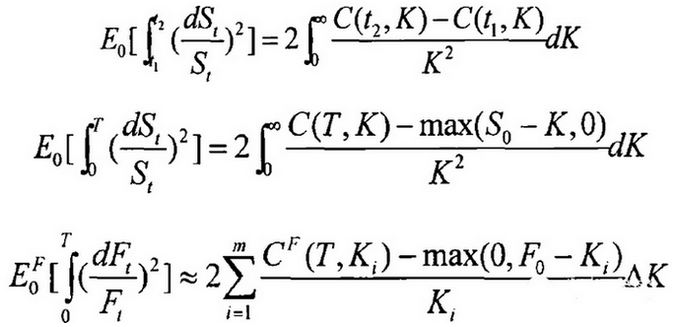

　　相对于传统的Black-Scholse隐含波动率(以下简称BSIV)，无模型隐含波动率(以下简称MFIV)的模型假设更为宽松，而且它用到了更多的期权合约，而BSIV一般是使用平价期权计算(其他期权涉及到波动率微笑的问题)。

　　虽然如此，但是MFIV也并不是完美的，它的主要技术问题是现实中的期权只有有限个，而且可能很少，而理论上的MFIV需要使用连续无穷的行权价的期权来计算。如此就产生了离散化的问题，一个是合约间距，一个是合约的多少。对于上述第3个式子，Jiang和Tian(2005)证明如下事实：(1)当Kmin和Kmax都在S±2σS时，截断误差可以忽略不计;(2)当ΔK<σS时，间距误差可以忽略不计。对沪深300，这相当于行权价在现价±800点，合约间距小于140点。后者可以满足，但是前者仍然差距很远，所以我们认为对国内的股指期权和个股期权而言，MFIV的使用可能仍有问题。

　　不仅如此，由于在MFIV中，各合约的权重是基本相当的，所以，平价合约占的权重相对较小，深度虚值的合约的波动率权重相对较大，而这些合约的价格受交易因素影响更大，价格变动非常剧烈，导致如此计算出来的波动率很可能波动较大。

　　现在CBOE的VIX指数使用的波动率算法就是MFIV的形势。

　　二、隐含波动率、历史波动率和未来波动率

　　大家计算波动率，一个主要的目标就是用来预测未来的波动率。　　从各种波动率的表现来看，有如下结论：

　　(1)隐含波动率较历史波动率高，美国2000年以来的VIX平均比GARCH波动率高，在波动率较低的时候差距更大，波动率大的时候反而差距较小;
(2)长期来看(3年以上)，隐含波动率和历史波动率的走势没有太大差别，其走势起伏同步;
(3)短期来看，隐含波动率和历史波动率差别较为明显，甚至某些时段走势相反;而且，隐含波动率显现出明显的领先性;
(4)不管隐含波动率还是历史波动率，都不能作为未来波动率的预测值，隐含波动率的走势明显滞后于未来波动率，甚至同步看来很多时候呈反向关系。所以，使用当前隐含波动率来作为未来波动率的预测表现极差;
(5)大部分的文献都表明，虽然隐含波动率不能作为未来波动率的预测，但是在对未来波动率的预测方面，隐含波动率仍然略好于历史波动率;
(6)我们认为预测未来的波动率和预测未来的股市是同等的难度。