t检验自由度的意义_t检验的效应量

大家在进行独立样本t检验分析时，往往只会报告t值、自由度、显著性水平。但现阶段，很多研究结果对t检验效应量的要求也很高。举个例子，检查两个班级的数学成绩，我们发现，二班的数学成绩显著高于一班，这个结果表述够清晰吗？

二班比一班高出多少分了呢？二班比一班高出10分，和二班比一班高出1分意义一样吗？如果每个班的数学成绩上下范围跨30分，而语文成绩上下范围仅跨5分，这两科成绩相差10分所代表的意义一样吗？这样看来，仅报告差异显著是不够的。

另外，t分数随着样本量的增加而增加，这样导致的显著性差异也需要不会受样本量影响的一个指标来反应处理效应的大小，这就是t检验的效应量。接下来咱们慢慢介绍。

独立效应t检验

t检验的效应量，我们用Cohen's d表示，简写为d，反映两个均数之间的标准差异：

其中分母是两个独立样本的联合标准差，计算方法为两个样本标准差的平方平均数，即

不过注意了，这是独立样本的计算方法，配对样本中共同标准差采用配对数据差值的标准差即可，不用这一公式。

得知怎么计算了，我们怎么在SPSS中操作呢？很可惜，目前SPSS并没有这一功能。那么平时我们怎么计算呢？

不用担心，在网上有个很便捷的效应量在线计算器，百度搜索“效应量计算器”，或直接登录网址http://www.99cankao.com/statistics/effect-of-size-calculator.php

其中既可以通过两组的描述统计结果得出效应量，也可以通过t值和自由度df得出。注意，d值和t值一样，有正负之分，一般我们取其绝对值进行报告。

【来颗栗子】

从一班和二班各抽10名同学，他们数学成绩如下，请报告其差异情况。

一班：85 80 80 85 90 88 90 88 80 75

二班：80 75 60 70 75 80 70 70 75 80

T检验如何操作考考大家，下面直接从t检验的输出结果讲。

描述统计的输出表中就有两组的均值和标准差。

双击表格，将对应数值复制到在线计算器中，点击计算，就会有相应的d值。

当然，用t值和df也可以得出相近结果。

由于小数的保留问题，两种计算方法无法保证得出完全相同的结果，但差别不会很大，两个结果均可以用于报告。结果上来看，t值差异显著，d =1.856，说明两个班的数学成绩差异显著，效应较高，差异很大。因此得出结论，一班的数学成绩显著高于二班。

（0.20以下：效应过小；0.20~0.50：效应偏小；0.50~0.80：效应较大；0.80以上：大效应）

配对样本t检验

在上文所提到的方法仅限于独立样本计算，因为相关样本中两两样本是配对的，其d分数的计算方法也相对简单些。

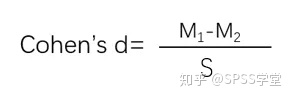
其中S是差值的平均数，这两个指标在SPSS配对样本t检验中表格可直接查阅。

通过公式直接进行计算即可，即

Cohen’s d =10.6/8.26=1.28

其实本质上理解，就是说一班的分数比二班大了一个多的标准差，这已经是很大的差距了。大家在学统计的过程中可以尝试用独特的方式进行理解，就会发现统计其实还有些许巧妙好玩呢~