构造一条二次bezier曲线_圆锥曲线第十八节：指标分裂与二次嵌入

目录：质点：圆锥曲线题目的三维矢量解法

写到这篇文章时，我发现我涉及到了一些我不会的知识。因此我以后把那些知识学完后可能会再修改这一节。

首先，我们对引入“指标分裂与二次嵌入”的动机作一个较长的铺垫。

我们在二次点列和二次对合一节已经初步认识了二次点列：二次点列是圆锥曲线上的点集。这类似于，一次点列是直线上的点集。在那一节我们看到，二次点列与一次点列间有许多相似性，这具体体现于：

1.二次点列与一次点列具有相同的拓扑 （由于加入了无穷远点，一次点列是紧致的）

2.二次点列中可以定义“交比”、“对合”、“调和点列”，与一次点列一样。

3.通过图中的方式，在圆锥曲线上任取一点

，则二次点列和某个一次线束可以一一对应。

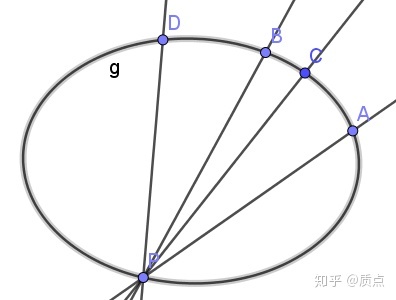
4.我们知道，线性子空间上的线性映射被称为射影变换。在经典的射影几何中，一个重要的内容就是讨论多个射影变换的复合——多个射影变换的复合仍然是射影变换。令人困惑的是下图的内容。设我们有两个一次线束

（中心点分别为

）。现在我们取出

中的一个元素，比如

。然后我们先作它与

的交点

（

到

的映射记为

），再作连线

（

到

的映射记为

），就得到了

中的一个元素。通过这样的构造，我们就得到了一个映射

，可以写作

。

这个映射是不是射影变换呢？看上去不应该是。

作为二次点列并不是线性子空间，因此

也不是线性映射。它们的复合映射自然也不必是线性映射，于是

不必是射影变换。然而这个结果是错的：由交比的不变性可以证明，

真的是射影变换！

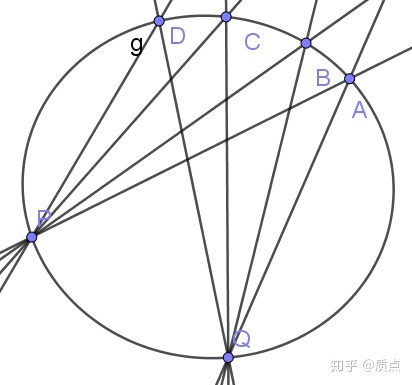
根据以上四条性质，我们发现，圆锥曲线上的二次点列在作图时可以无缝融入一次点列。事实上，经典射影几何的教材中有许多定理正是建立于此。但是，这是为什么？以上四条性质的核心在于这个结论：

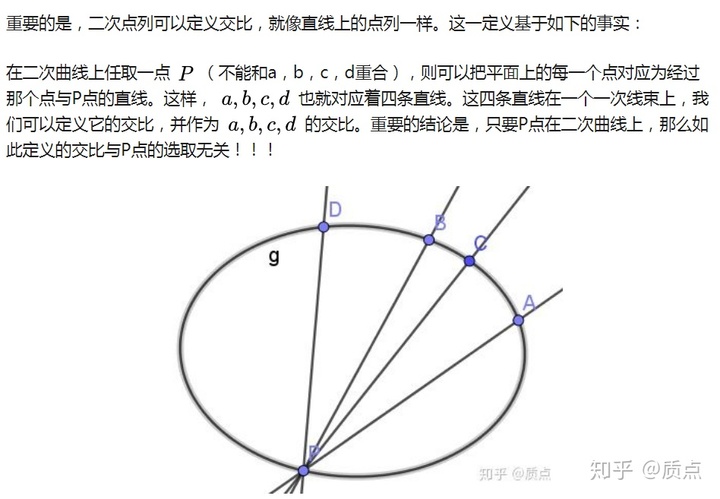
我们在二次点列和二次对合中给出了证明。这一证明虽然正确，但是并不自然，就像是某个巧合一样。况且从另一个角度，二次点列与一次点列仍有十分明显的不同之处：

1.一次点列是平面的线性子空间，而二次点列并不是平面的线性子空间。

2.之前第4条所说的

，虽然和射影变换有相似之处，但毕竟不是射影变换。其核心就是：

一次点列与二次点列间的一一映射是非线性的。

这种“非线性”带来的后果就是二次点列的代数意义不明确。它就像是一次点列间射影变换的某个中间产物。

一次点列的代数意义是很明确的，因为它就是三维线性空间中的二维子空间中的元素。而利用其“二维线性空间”的背景，可以构造出其中的交比、