容斥原理和抽屉原理

转自：http://www.exam8.com/zige/gongwuyuan/xingzheng/sl/201408/2984187.html

一、容斥原理

　　在计数时，要保证无一重复，无一遗漏。为了使重叠部分不被重复计算，在不考虑重叠的情况下，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

　　1.容斥原理1——两个集合的容斥原理

　　如果被计数的事物有A、B两类，那么，先把A、B两个集合的元素个数相加，发现既是A类又是B类的部分重复计算了一次，所以要减去。如图所示：

　　公式：A∪B=A+B-A∩B

　　

 

　　总数=两个圆内的-重合部分的

　　【例1】一次期末考试，某班有15人数学得满分，有12人语文得满分，并且有4人语、数都是满分，那么这个班至少有一门得满分的同学有多少人?

　　数学得满分人数→A，语文得满分人数→B，数学、语文都是满分人数→A∩B，至少有一门得满分人数→A∪B。A∪B=15+12-4=23，共有23人至少有一门得满分。

　　2.容斥原理2——三个集合的容斥原理

　　如果被计数的事物有A、B、C三类，那么，将A、B、C三个集合的元素个数相加后发现两两重叠的部分重复计算了1次，三个集合公共部分被重复计算了2次。

　　如图所示，灰色部分A∩B-A∩B∩C、B∩C-A∩B∩C、C∩A-A∩B∩C都被重复计算了1次，黑色部分A∩B∩C被重复计算了2次，因此总数A∪B∪C=A+B+C-(A∩B-A∩B∩C)-(B∩C-A∩B∩C)-(C∩A-A∩B∩C)-2A∩B∩C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C。即得到：

　　公式：A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C

　　

 

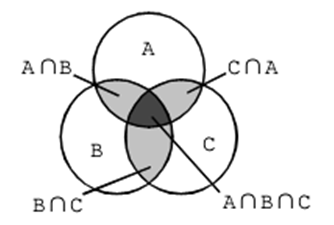
　　总数=三个圆内的-重合两次的+重合三次的

　　【例2】某班有学生45人，每人都参加体育训练队，其中参加足球队的有25人，参加排球队的有22人，参加游泳队的有24人，足球、排球都参加的有12人，足球、游泳都参加的有9人，排球、游泳都参加的有8人，问：三项都参加的有多少人?

　　参加足球队→A，参加排球队→B，参加游泳队→C，足球、排球都参加的→A∩B，足球、游泳都参加的→C∩A，排球、游泳都参加的→B∩C，三项都参加的→A∩B∩C。三项都参加的有A∩B∩C=A∪B∪C-A-B-C+A∩B+B∩C+C∩A=45-25-22-24+12+9+8=3人。

　　3.用文氏图解题

　　文氏图又称韦恩图，能够将逻辑关系可视化的示意图。从文氏图可清晰地看出集合间的逻辑关系、重复计算的次数，最适合描述3个集合的情况。

　　【例3】某班有50 位同学参加期末考试，结果英文不及格的有15 人，数学不及格的有19 人，英文和数学都及格的有21 人。那么英文和数学都不及格的有( )人。

　　A.4 B.5 C.13 D.17

　　解析：如图所示，按英文及格、数学及格画2个圆圈，根据题干条件确定它们重叠。

　　

 

　　二、抽屉原理

　　能利用抽屉原理来解决的问题称为抽屉问题。在行测考试数学运算中，考查抽屉原理问题时，题干通常有“至少……，才能保证……”字样。

　　抽屉原理1

　　将多于n件的物品任意放到n个抽屉中，那么至少有一个抽屉中的物品件数不少于2。(至少有2件物品在同一个抽屉)

　　抽屉原理2

　　将多于m×n件的物品任意放到n个抽屉中，那么至少有一个抽屉中的物品的件数不少于m+1。(至少有m+1件物品在同一个抽屉)

　　下面我们通过几个简单的例子来帮助理解这两个抽屉原理。

　　【例1】将5件物品放到3个抽屉里，要想保证任一个抽屉的物品最少，只能每个抽屉放一件，有5件物品，放了3件，还剩5-3×1=2件，这两件只能分别放入两个抽屉中，这样物品最多的抽屉中也只有2件物品中公.教育版权。

　　即当物品数比抽屉数多时，不管怎么放，总有一个抽屉至少有2件物品。

　　【例2】将10件物品放到3个抽屉里呢?将22件物品放到5个抽屉里呢?

　　同样，按照前面的思路，要想保证任一个抽屉的物品数都最少，那么只能先平均放。

　　10÷3=3……1，则先每个抽屉放3件，还剩余10-3×3=1件，随便放入一个抽屉中，则这个抽屉中的物品数为3+1=4件。

　　22÷5=4……2，则先每个抽屉放4件，还剩余22-4×5=2件，分别放入两个抽屉中，则这两个抽屉中的物品数为4+1=5件。

　　即如果物体数大于抽屉数的m倍，那么至少有一个抽屉中的物品数不少于m+1。

　　1.利用抽屉原理解题

　　一般来说，求抽屉数、抽屉中的最多有几件物品时采用抽屉原理，其解题流程如下：

　　(1)找出题干中物品对应的量;

　　(2)合理构造抽屉(简单问题中抽屉明显，找出即可);

　　(3)利用抽屉原理1、抽屉原理2解题。

　　【例题1】外国讲星座，中国传统讲属相。请问在任意的37个中国人中至少有几个人的属相相同?

　　A.3 B.4 C.5 D.6

　　解析： 属相有12种，看成12个抽屉，则至少有一个抽屉有不少于 =4个人，即至少有4个人属相相同，选B。

 

　　2.考虑最差(最不利)情况

　　抽屉问题所求多为极端情况，即从最差的情况考虑。对于“一共有n个抽屉，要有(取)多少件物品，才能保证至少有一个抽屉中有m个物体”，即求物品总数时，考虑最差情况这一方法的使用非常有效。具体思路如下：

　　最差情况是尽量不能满足至少有一个抽屉中有m个物品，因此只能将物品均匀放入n个抽屉中。当物品总数=n×(m-1)时，每个抽屉中均有m-1个物品，此时再多1个，即可保证有1个抽屉中有m个物品。因此物品总数为n×(m-1)+1。

　　【例题2】从一副完整的扑克牌中，至少抽出多少张牌，才能保证至少有6张牌的花色相同?

　　A.21 B.22 C.23 D.24

　　解析：此题答案为C。一副完整的扑克牌包括大王、小王;红桃、方块、黑桃、梅花各13张。

　　至少抽出多少张牌→求取物品的件数，考虑最差情况中公.教育版权。

　　要求6张牌的花色相同，最差情况即红桃、方块、黑桃、梅花各抽出5张，再加上大王、小王，此时共取出了4×5+2=22张，此时若再取一张，则一定有一种花色的牌有6张。即至少取出23张牌，才能保证至少6张牌的花色相同。

转载于:https://www.cnblogs.com/limingluzhu/p/5763054.html