[NOIP 2015] 斗地主 landlord

想起几个月之前的 noip2015…只会瞎搞…这道题骗了 30 分。T T

题目

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的 A 到 K 加上大小王的共 54 张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2< 小王 < 大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 n 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。
　　现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。
　　需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。
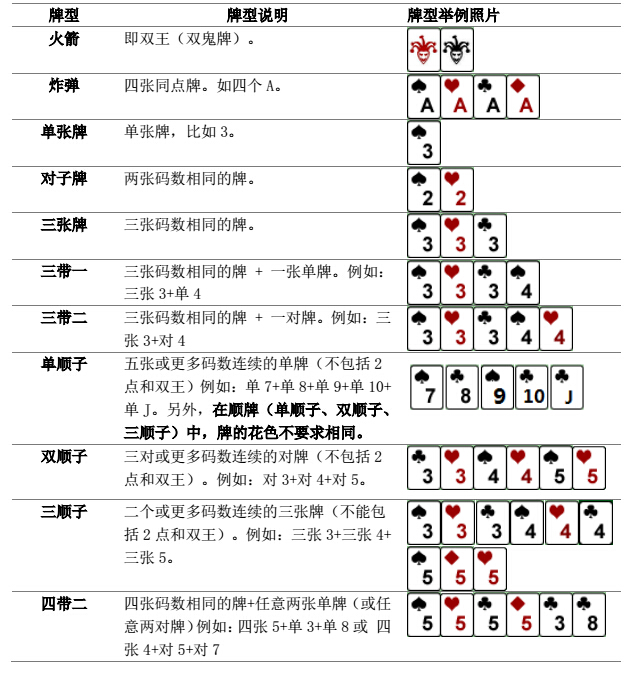
　　具体规则如下：

---

其实看起来不好做，一顿乱搞就行了…

好吧承认还是瞄了一眼题解。大概是：先枚举所有的顺子的情况，然后对剩下的单张、对子、三张、四张贪心一下…

放代码：

#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;

const int L[] = {0, 4, 2, 1}, INF = 0x3f3f3f3f;
int card[20];   //牌的张数，王 = 0，2 = 2, 3 = 3, ... K = 13, A = 14 
int cnt[5];     //统计单张、对子、三张、四张的个数。
int ans; 

//不考虑各种顺子的手数 
int calc(){
    memset(cnt, 0, sizeof(cnt));
    for(int i = 2; i <= 14; ++i){
        ++cnt[card[i]];
    }
    cnt[1] += card[0];
    int ret = cnt[3] + cnt[4], tmp;

    tmp = min(cnt[4], cnt[2] >> 1);
    cnt[4] -= tmp; cnt[2] -= tmp << 1;
    tmp = min(cnt[4], cnt[1] >> 1);
    cnt[4] -= tmp; cnt[1] -= tmp << 1;

    if(cnt[2] || cnt[1]){
        tmp = min(cnt[3], cnt[2]);
        cnt[3] -= tmp; cnt[2] -= tmp;
        tmp = min(cnt[3], cnt[1]);
        cnt[3] -= tmp; cnt[1] -= tmp;
    }

    ret += cnt[1] + cnt[2];
    if(cnt[1] >= 2 && card[0] == 2) --ret;
    return ret;
}

//hnd：已经使用的手数
//w：顺子的宽度（1 <= w <= 3） 
void dfs(int hnd, int w, int depth){
    if(w < 1) return;
/*  
    for(int i = 0; i < depth; ++i) printf("--");
    printf("hands = %d, w = %d\n", hnd, w);
    for(int i = 0; i <= 14; ++i) printf("%d ", card[i]);
    printf("\n");
*/
    ans = min(ans, calc() + hnd);
    dfs(hnd, w - 1, depth + 1);

    int head = -1;  //顺子头 
    for(int i = 3; i <= 14; ++i){
        if(card[i] >= w){
            if(head == -1) head = i;
            else if(i >= head + L[w]){
                for(int j = head; j <= i; card[j++] -= w);
                for(int j = head; j <= i; card[j++] += w){
                    if(i >= j + L[w]) dfs(hnd + 1, w, depth + 1);
                }
            }
        } else {
            head = -1;
        }
    }
}

int main(){
//  freopen("in.txt", "r", stdin);

    int T, N, a, b;
    scanf("%d%d", &T, &N);
    while(T--){
        memset(card, 0, sizeof(card));
        ans = INF;
        for(int i = 0; i < N; ++i){
            scanf("%d%d", &a, &b);
            if(a == 1) a = 14;
            ++card[a];
        }

        dfs(0, 3, 0);
        printf("%d\n", ans);
    }
    return 0;
}

转载于:https://www.cnblogs.com/will7101/p/6506691.html