算法精解：DAG有向无环图

最新推荐文章于 2024-05-19 18:51:10 发布

weixin_30733003

最新推荐文章于 2024-05-19 18:51:10 发布

阅读量221

点赞数

文章标签： java 数据结构与算法区块链

原文链接：http://www.cnblogs.com/jfdwd/p/11095188.html

版权

DAG是公认的下一代区块链的标志。本文从算法基础去研究分析DAG算法，以及它是如何运用到区块链中，解决了当前区块链的哪些问题。

关键字：DAG，有向无环图，算法，背包，深度优先搜索，栈，BlockChain，区块链

图

图是数据结构中最为复杂的一种，我在上大学的时候，图的这一章会被老师划到考试范围之外，作为我们的课后兴趣部分。但实际上，图在信息化社会中的应用非常广泛。图主要包括：

无向图，结点的简单连接
有向图，连接有方向性
加权图，连接带有权值
加权有向图，连接既有方向性，又带有权值

图是由一组顶点和一组能够将两个顶点相连的边组成。

常见的地图，电路，网络等都是图的结构。

术语

顶点：图中的一个点
边：连接两个顶点的线段叫做边，edge
相邻的：一个边的两头的顶点称为是相邻的顶点
度数：由一个顶点出发，有几条边就称该顶点有几度，或者该顶点的度数是几，degree
路径：通过边来连接，按顺序的从一个顶点到另一个顶点中间经过的顶点集合
简单路径：没有重复顶点的路径
环：至少含有一条边，并且起点和终点都是同一个顶点的路径
简单环：不含有重复顶点和边的环
连通的：当从一个顶点出发可以通过至少一条边到达另一个顶点，我们就说这两个顶点是连通的
连通图：如果一个图中，从任意顶点均存在一条边可以到达另一个任意顶点，我们就说这个图是个连通图
无环图：是一种不包含环的图
稀疏图：图中每个顶点的度数都不是很高，看起来很稀疏
稠密图：图中的每个顶点的度数都很高，看起来很稠密
二分图：可以将图中所有顶点分为两部分的图

所以树其实就是一种无环连通图。

有向图

有向图是一幅有方向性的图，由一组顶点和有向边组成。所以，大白话来讲，有向图是包括箭头来代表方向的。

常见的例如食物链，网络通信等都是有向图的结构。

术语

上面我们介绍了顶点的度数，在有向图中，顶点被细分为了：

出度：由一个顶点出发的边的总数
入度：指向一个顶点的边的总数

接着，由于有向图的方向性，一条边的出发点称为头，指向点称为尾。

有向路径：图中的一组顶点可以满足从其中任意一个顶点出发，都存在一条有向边指向这组顶点中的另一个。
有向环：至少含有一条边的起点和终点都是同一个顶点的一条有向路径。
简单有向环：一条不含有重复顶点和边的环。
路径或环的长度就是他们包含的边数。

图的连通性在有向图中表现为可达性，由于边的方向性，可达性必须是通过顶点出发的边的正确方向，与另一个顶点可连通。

邻接表数组

可表示图的数据类型，意思就是如何通过一个具体的文件内容，来表示出一幅图的所有顶点，以及顶点间的边。

邻接表数组，以顶点为索引（注意顶点没有权值，只有顺序，因此是从0开始的顺序值），其中每个元素都是和该顶点相邻的顶点列表。

5 vertices, 3 edges
0: 4 1 1: 0 2: 3: 4:

背包

做一个背包集合，用来存储与一个顶点连通的顶点集合，因为不在意存储顺序，并且只进不出，所以选择背包结构来存储。温习一下背包

package algorithms.bag;

import java.util.Iterator;

// 定义一个背包集合，支持泛型，支持迭代
public class Bag<Item> implements Iterable<Item> { private class BagNode<Item> { Item item; BagNode next; } BagNode head; int size; @Override public Iterator<Item> iterator() { return new Iterator<Item>() { BagNode node = head; @Override public boolean hasNext() { return node.next != null; } @Override public Item next() { Item item = (Item) node.item; node = node.next; return item; } }; } public Bag() { head = new BagNode(); size = 0; } // 往前插入 public void add(Item item) { BagNode temp = new BagNode(); // 以下两行代码一定要声明，不可直接使用temp = head，那样temp赋值的是head的引用，对head的所有修改会直接同步到temp，temp就不具备缓存的功能，引发bug。。 temp.next = head.next; temp.item = head.item; head.item = item; head.next = temp; size++; } public boolean isEmpty() { return size == 0; } public int size() { return this.size; } public static void main(String[] args) { Bag<String> bags = new Bag(); bags.add("hello"); bags.add("yeah"); bags.add("liu wen bin"); bags.add("seminar"); bags.add("1243"); System.out.println(bags.size); // for (Iterator i = bags.iterator(); i.hasNext(); ) { // System.out.println(i.next()); // } // 由于Bag实现了Iterable接口，所以支持以下方式遍历 for (String a : bags) { System.out.println(a); } } }

有向图结构

下面代码实现一个有向图数据结构，并添加常用有向图属性和功能。

package algorithms.graph;

import algorithms.bag.Bag;
import ioutil.In;
import ioutil.StdOut;

import java.io.FileReader; public class Digraph { private final int V;// 顶点总数，定义final，第一次初始化以后不可更改。 private int E;// 边总数 private Bag<Integer>[] adj;// {邻接表}顶点为数组下标，值为当前下标为顶点值所连通的顶点个数。 public Digraph(int v) { this.V = v; this.E = 0; adj = new Bag[V]; for (int i = 0; i < V; i++) { adj[i] = new Bag<Integer>(); } } public Digraph(In in) { this(in.readInt()); int E = in.readInt(); for (int i = 0; i < E; i++) { int v = in.readInt(); int w = in.readInt(); addEdge(v, w); } } public int V() { return this.V; } public int E() { return this.E; } /** * v和w是两个顶点，中间加一条边，增加稠密度。 * * @param v 大V是顶点总数，v是顶点值，所以并v不存在大小限制 * @param w 同上。 */ public void addEdge(int v, int w) { adj[v].add(w); E++; } /** * 返回一个顶点的连通顶点集合的迭代器 * * @param v * @return Bag本身就是迭代器，所以返回该顶点的连通顶点集合Bag即可。 */ public Iterable<Integer> adj(int v) { return adj[v]; } /** * 将图中所有方向反转 * * @return 返回一个图将所有方向反转后的副本 */ public Digraph reverse() { Digraph R = new Digraph(V); for (int v = 0; v < V; v++) { for (int w : adj[v]) {// 遍历原图中跟v顶点连通的顶点w。 R.addEdge(w, v); } } return R; } /** * 按照邻接表数组结构输出有向图内容 * * @return */ public String toString() { String s = V + " vertices, " + E + " edges\n"; for (int v = 0; v < V; v++) { s += v + ": "; for (int w : this.adj(v)) { s += w + " "; } s += "\n"; } return s; } public static void main(String[] args) { Digraph d = new Digraph(5); d.addEdge(0, 1); d.addEdge(1, 0); d.addEdge(2, 3); d.addEdge(0, 4); StdOut.println(d); /** 输出： 5 vertices, 3 edges 0: 4 1 1: 0 2: 3: 4: */ } }

以上背包和有向图代码相关解释请具体参照代码中注释。

可达性

上面提到了有向图中的可达性和图中的连通性的关系，可达性是连通性的特殊形式，对方向敏感，所以提到有向图，不可不研究可达性。

可达性解答了“从一个顶点v到达另一个顶点w，是否存在一条有向路径”等类似问题。

深度优先搜索

解答可达性问题，要借助深度优先搜索算法。为了更好的理解深度优先算法，先来搞清楚如何完全探索一个迷宫。

Tremaux搜索

完全探索一个迷宫的规则是：从起点出发，不走重复路线，走到终点走出迷宫。具体流程：

每当第一次到达一个新的顶点或边时，标记上。
在走的过程中，遇到一个已标记的顶点或边时，退回到上一个顶点。
当回退到的顶点已没有可走的边时继续回退。

我想Tremaux搜索会给我们带来一些启发，回到图的深度优先搜索算法。

package algorithms.graph;

import algorithms.bag.Bag;
import ioutil.StdOut;

/**
 * 基于深度优先搜索（Depth First Search）解答有向图顶点可达性问题。
 */
public class DigraphDFS { private boolean[] marked;// 是否标记过 /** * 算法：在图中找到从某个顶点出发的所有顶点 * * @param digraph * @param start */ public DigraphDFS(Digraph digraph, int start) { marked = new boolean[digraph.V()];// 初始化marked数组 dfs(digraph, start); } /** * 算法：在图中找到从某些顶点出发的所有顶点，这些顶点被作为一个集合传入。 * * @param digraph * @param startSet */ public DigraphDFS(Digraph digraph, Iterable<Integer> startSet) { marked = new boolean[digraph.V()]; for (int w : startSet) { dfs(digraph, w); } } /** * 查询某个顶点是否被标记（是否可达，因为标记过就是可达的） * * @param v * @return */ public boolean marked(int v) { return marked[v]; } /** * 深度优先搜索核心算法，通过标记，在图中从v顶点出发找到有效路径 * <p> * 返回的是通过标记形成的一条有效路径。 * * @param digraph * @param v */ private void dfs(Digraph digraph, int v) { marked[v] = true;// 标记起点可达。 for (int w : digraph.adj(v)) {// 遍历v顶点可达的一级顶点。 if (!marked[w]) dfs(digraph, w);// 如果发现w顶点未到达过，则继续从w开始dfs（即向前走了一步） } } public static void main(String[] args) { Digraph d = new Digraph(5);// 初始化五个顶点的图 d.addEdge(0, 1); d.addEdge(1, 0); d.addEdge(2, 3); d.addEdge(0, 4); Bag<Integer> startSet = new Bag<>(); startSet.add(2); DigraphDFS reachable = new DigraphDFS(d, startSet); for (int v = 0; v < d.V(); v++) { if (reachable.marked(v)) { StdOut.print(v + " "); } StdOut.println(); } /** * 输出： * 2 3 */ } }

startSet是入参条件，只有一个值为2，即在图中找寻2的有效路径，通过图中的边我们可以看出，2的有效路径只有3，所以输出是正确的。

可达性的一种应用：垃圾收集

我们都知道一般的对象垃圾收集都是计算它的引用数。在图结构中，把对象作为顶点，引用作为边，当一个对象在一段时间内未被他人引用的时候，这个顶点就是孤立的，对于其他有效路径上的顶点来说它就是不可达的，因此就不会被标记，这时候，例如JVM就会清除掉这些对象释放内存，所以JVM也是一直在跑类似以上这种DFS的程序，不断找到那些未被标记的顶点，按照一定时间规则进行清除。

有向无环图

不包含有向环的有向图就是有向无环图，DAG，Directed Acyclic Graph。

上面我们循序渐进的介绍了图，有向图，本节开始介绍有向无环图，概念也已经给出，可以看出有向无环图是有向图的一种特殊结构。那么第一个问题就是

如何监测有向图中没有有向环，也就是如何确定一个DAG。

寻找有向环

基于上面的问题，我们要做一个寻找有向环的程序，这个程序还是依赖DFS深度优先搜索算法，如果找不到，则说明这个有向图是DAG。

栈

先来补个坑，其实前面包括背包我在之前都写过，但因为前面那篇文章是我第一篇博文，我还太稚嫩，没有掌握好的编辑器，也没有粘贴代码，所以这里有必要重新填坑。

package algorithms.stack;

import ioutil.StdOut;

import java.util.Iterator;
import java.util.NoSuchElementException;

public class Stack<Item> implements Iterable<Item> { private int SIZE; private Node first;// 栈顶 public Stack() {// 初始化成员变量 SIZE = 0; first = null; } private class Node { private Item item; private Node next; } // 栈：往first位置插入新元素 public void push(Item item) { Node temp = first; first = new Node(); first.item = item; first.next = temp; SIZE++; } // 栈：从first位置取出新元素，满足LIFO，后进先出。 public Item pop() { if (isEmpty()) throw new RuntimeException("Stack underflow"); Item item = first.item; first = first.next; SIZE--; return item; } public boolean isEmpty() { return first == null; } public int size() { return this.SIZE; } @Override public Iterator<Item> iterator() { return new Iterator<Item>() { Node node = first; @Override public boolean hasNext() { return first != null; } @Override public Item next() { if (!hasNext()) throw new NoSuchElementException(); Item item = node.item; node = node.next; return item; } }; } public static void main(String[] args){ Stack<String> stack = new Stack<>(); stack.push("heyheyhey"); stack.push("howau"); stack.push("231"); StdOut.println(stack.SIZE); StdOut.println(stack.pop()); } }

我们要做寻找有向环的程序的话，要依赖栈的结构，所以上面把这个坑给填了，下面回归到寻找有向环的程序。（当然，你也可以直接使用java.util.Stack类）

package algorithms.graph;

import ioutil.StdOut;

import java.util.Stack;

public class DirectedCycle { private boolean[] marked;// 以顶点为索引，值代表了该顶点是否标记过（是否可达） private Stack<Integer> cycle; // 用来存储有向环顶点。 // *****重点理解这里start**** private int[] edgeTo;// edgeTo[0]=1代表顶点1->0, to 0的顶点为1。 // *****重点理解这里end**** private boolean[] onStack;// 顶点为索引，值为该顶点是否参与dfs递归，参与为true public DirectedCycle(Digraph digraph) { // 初始化成员变量 marked = new boolean[digraph.V()]; onStack = new boolean[digraph.V()]; edgeTo = new int[digraph.V()]; cycle = null; // 检查是否有环 for (int v = 0; v < digraph.V(); v++) { dfs(digraph, v); } } private void dfs(Digraph digraph, int v) { onStack[v] = true;// 递归开始，顶点上栈 marked[v] = true; for (int w : digraph.adj(v)) {// 遍历一条边，v-> w // 终止条件：找到有向环 if (hasCycle()) return; // 使用onStack标志位来记录有效路径上的点，如果w在栈上，说明w在前面当了出发点， if (!marked[w]) { edgeTo[w] = v;// to w的顶点为v dfs(digraph, w); } else if (onStack[w]) {// 如果指到了已标记的顶点，且该顶点递归栈上。（栈上都是出发点，而找到了已标记的顶点是终点，说明出发点和终点相同了。） cycle = new Stack<Integer>(); for (int x = v; x != w; x = edgeTo[x]) {//起点在第一次循环中已经push了，不要重复 cycle.push(x);// 将由v出发，w结束的环上中间的结点遍历push到cycle中。 } cycle.push(w);// push终点 } } onStack[v] = false;// 当递归开始结算退出时，顶点下栈。 } public boolean hasCycle() { return cycle != null; } public Iterable<Integer> cycle() { return cycle; } public static void main(String[] args) { Digraph d = new Digraph(6); d.addEdge(0, 1); d.addEdge(1, 2); d.addEdge(2, 3); d.addEdge(3, 0); DirectedCycle directedCycle = new DirectedCycle(d); if (directedCycle.hasCycle()) { for (int a : directedCycle.cycle()) { StdOut.println(a); } } else { StdOut.println("DAG"); } } }

这段代码不长但其中算法比较复杂，我尽力在注释中做了详细解释，如有任何不明之处，欢迎随时留言给我。

以上程序的测试用图为

6 vertices, 4 edges
0: 1 
1: 2 2: 3 3: 0 4: 5:

肉眼可以看出，这是一个0-1-2-3-0的一个有向环，所以以上程序的执行结果为：

先入栈的在后面，可以看出是0-1-2-3的有向环结构。如果我们将图的内容改为：

6 vertices, 4 edges
0: 1 
1: 2 2: 3 3: 4: 5: 0

则明显最后一个拼图3-0被我们打破了，变成了无所谓的5-0，这时该有向图就不存在有向环。此时以上程序执行结果为：

DAG

DAG与BlockChain

上面一章节我们将DAG深挖了挖，我想到这里您已经和我一样对DAG的算法层面非常了解，那么它和如今沸沸扬扬的区块链有什么关联呢？本章节主要介绍这部分内容。

在前面的文章中，我们已经了解了区块链技术，无论是比特币还是以太坊，都是基于一条链式结构，实现了去中心化的，点对点的，trustless的一种新型技术。然而这条链式结构在面临业务拓展的时候屡屡遭受新的挑战，例如块存储量问题，交易速度问题，数据总量过大，单节点存储压力等等。而DAG是基于图的一种实现方式，之所以不允许有向环的出现，是因为DAG可以保证结点交易的顺序，可以通过上面介绍过的有效路径来找到那根主链。如果出现了有向环，那系统就乱了。如果没有有向环的话，DAG中可以有多条有效路径连接各个顶点，因此DAG可以说是更加完善，强大的新一代区块链结构。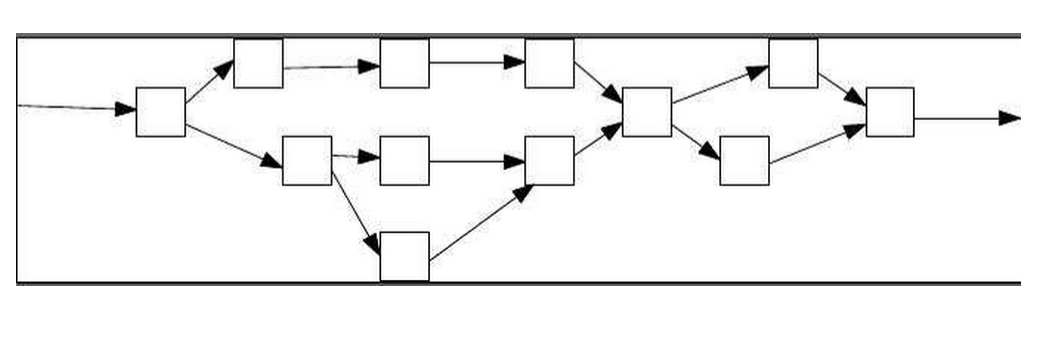

目前非常有名的采用DAG技术的区块链产品有DagCoin,IOTA,ByteBall等，他们都是基于DAG，在性能和储量上面有了全面的提升。

这里面仍然会有“分叉”的可能，处理方式也是相同的，看哪个结点能够有新的后续，这个部分我们在讲“叔块”的时候说过。

区块链采用DAG结构以后称为了blockless，无块化的结构，即我们不再将交易打包到块中，以块为单元进行存储，而是直接将交易本身作为基本单元进行存储。另外，DAG也有双花的可能，也是上面“分叉问题”引起的，但它在确认有效路径以后会自动恢复。同时，DAG是异步共识，具体机制还不了解，但它解决了交易性能问题。