用计算机画有常数的函数图像,函数图像

在数学中，函数 f 的图形(或图象)指的是所有有序对(x, f(x))组成的集合[1]。具体而言，如果x为实数，则函数图形在平面直角坐标系上呈现为一条曲线。如果函数自变量x为两个实数组成的有序对(x1, x2)，则图形就是所有三重序(x1, x2, f(x1, x2))组成的集合，呈现为曲面(参见三维计算机图形)。

中文名

函数图象

外文名

Functions images图象性质

满足等式：y=kx+b

应    用

水量g是抽水时间t的一次函数

函数图像几何与方程论

编辑

语音

Functions images(函数的图象)

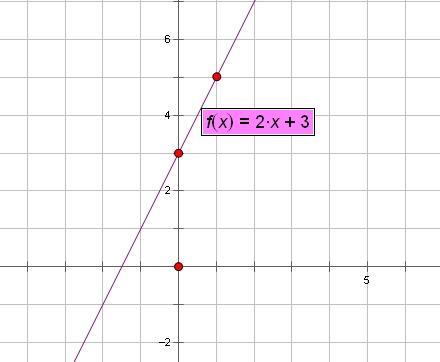
一次函数图像点集{(x，y)丨y=x}叫做函数y=x的图象

一次函数

自变量x和因变量y有如下关系：

y=kx+b(k，b为常数，k≠0)

则称y是x的一次函数。

特别地，当b=0时，y是x的正比例函数。

若两个变量x，y间的关系式可以表示为y=kx+b(k，b为常数，k≠0)的形式，则称y是x的一次函数(x为自变量，y为因变量)。特别地，当b=0时，称y是x的正比例函数。

函数图像图象性质

1． 作法与图形：通过如下3个步骤(1)算出该函数图象与Y轴和X轴的交点的坐标(2)描点；(3)连线，可以作出一次函数的图象——一条直线。

2． 性质：在一次函数上的任意一点P(x，y)，都满足等式：y=kx+b。

3． k，b与函数图象所在象限。

当k>0时，直线必通过一、三象限，从左往右，y随x的增大而增大；

当k<0时，直线必通过二、四象限，从左往右，y随x的增大而减小；

当b>0时，直线必通过一、二象限；当b<0时，直线必通过三、四象限。

特别地，当b=O时，直线通过原点O(0，0)表示的是正比例函数的图象。

这时，当k>0时，直线只通过一、三象限；当k<0时，直线只通过二、四 象限。

反比例函数图像4. (1) 函数关系中自变量可取值的集合叫做函数的定义域。求用解析式表示的函数的定义域，就是求使函数各个组成部分有意义的集合的交集，对实际问题中函数关系定义域，还需要考虑实际问题的条件。 (2)值域与定义域内的所有x值对应的函数值形成的集合，叫做函数的值域。(3)单调性定义：对于给定区间上的函数f(x)。

函数图像例题

已知点A(x1，y1)；B(x2，y2)，请确定过点A、B的一次函数的表达式。 (1)设一次函数的表达式(也叫解析式)为y=kx+b。如果b=0，则函数解析式为y=kx,所以说正比例函数是特殊的一次函数。 (2)因为在一次函数上的任意一点P(x，y)，都满足等式y=kx+b。所以可以列出2个方程： y1=kx1+b① 和y2=kx2+b②。 (3)解这个二元一次方程，得到k，b的值。 (4)最后得到一次函数的表达式。 (5)在y=kx+b中,使x,y分别等于0，可求出两个坐标系必定经过的两点(0,b)和(-b/k,0)。

函数图像应用

编辑

语音

1.当时间t一定，距离S是速度v的一次函数。S=vt。

2.当水池抽水速度f一定，水池中水量g是抽水时间t的一次函数。设水池中原有水量S。g=S-ft。

函数图像分类

编辑

语音

一次函数

正比例函数

函数图像反比例函数

形如 y=k/x(k为常数且k≠0) 的函数，叫做反比例函数。

自变量x的取值范围是不等于0的一切实数。

如图，上面给出了x分别为正和负(2和-2), k=4 时的函数图象。

函数图像双钩函数

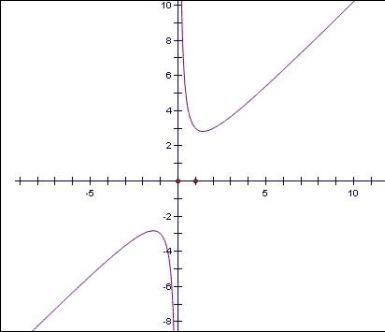
双钩函数图像函数f(x)=ax+b/x,(a>0,b>0)叫做双钩函数。

该函数是奇函数，图象关于原点对称。位于第一、三象限。

当x>0时，由基本不等式可得：y ≥2√ab

当且仅当ax=b/x,即x=√(b/a)时取等号。

故其顶点坐标为(√(b/a)，2√ab)，图象在(0，√(b/a))上是单调递减的，在(√(b/a)，+∝)上是单调递增

同理：当x<0时，由基本不等式可得：y≤-2√ab

当且仅当ax=b/x,即x=-√(b/a)时取等号。

故其顶点坐标为(-√(b/a)，-2√ab)，

图象在(-∝，-√(b/a))上是单调递增，

在(-√(b/a)，0)上是单调递减的。

当a<0,b<0 时可转化为a>0,b>0的情况

通常，作图时，x看做0。代入得y，也就是纵轴坐标(0，y)

有时，通过平移，把形如y=(ax+b)/(cx+d)也看成反比例函数。

特殊位置关系

当平面直角坐标系中两直线平行时，其函数解析式中K值(即一次项系数)相等

当平面直角坐标系中两直线垂直时，其函数解析式中K值互为负倒数(即两个K值的乘积为-1)

函数图像二次函数

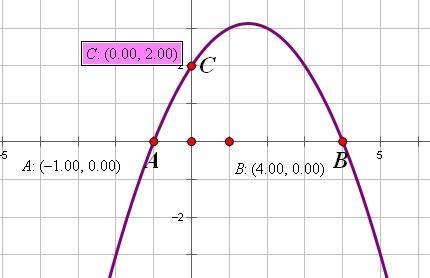
二次函数图像一般地，自变量x和因变量y之间存在如下关系：y=ax^2+bx+c

(a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.)

则称y为x的二次函数。

二次函数表达式的右边通常为二次三项式。

表达式

一般式：y=ax^2+bx+c(a，b，c为常数，a≠0)

顶点式：y=a(x-h)^2+k [抛物线的顶点P(h，k)]

交点式：y=a(x-x₁)(x-x ₂) [仅限于与x轴有交点A(x₁ ，0)和 B(x₂，0)的抛物线]

注：在3种形式的互相转化中，有如下关系:

h=-b/2a k=(4ac-b^2)/4a x₁,x₂=(-b±√b^2-4ac)/2a

图象

在平面直角坐标系中作出二次函数y=x^2的图象，

可以看出，二次函数的图象是一条抛物线。

性质

1.抛物线是轴对称图形。对称轴为直线x = -b/2a。

对称轴与抛物线唯一的交点为抛物线的顶点P。

特别地，当b=0时，抛物线的对称轴是y轴(即直线x=0)

2.抛物线有一个顶点P，坐标为P ( -b/2a ，(4ac-b^2)/4a )

当-b/2a=0时，P在y轴上；当Δ= b^2-4ac=0时，P在x轴上。

3.二次项系数a决定抛物线的开口方向和大小。

当a>0时，抛物线向上开口；当a<0时，抛物线向下开口。

|a|越大，则抛物线的开口越小。

4.一次项系数b和二次项系数a共同决定对称轴的位置。

当a与b同号时(即ab>0)，对称轴在y轴左；

当a与b异号时(即ab<0)，对称轴在y轴右。

5.常数项c决定抛物线与y轴交点。

抛物线与y轴交于(0，c)

6.抛物线与x轴交点个数

Δ= b方-4ac>0时，抛物线与x轴有2个交点。

Δ= b方-4ac=0时，抛物线与x轴有1个交点。

Δ= b方-4ac<0时，抛物线与x轴没有交点。X的取值是虚数(x= -b±√b^2－4ac 的值的相反数，乘上虚数i，整个式子除以2a)

位置关系

二次函数y=ax^2，y=a(x-h)^2，y=a(x-h)^2 +k，y=ax^2+bx+c(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

解析式 顶点坐标 对 称 轴

y=ax^2 (0，0) x=0

y=a(x-h)^2 (h，0) x=h

y=a(x-h)^2+k (h，k) x=h

y=ax^2+bx+c (-b/2a，[4ac-b^2]/4a) x=-b/2a

当h>0时，y=a(x-h)^2的图象可由抛物线y=ax^2向右平行移动h个单位得到，

当h<0时，则向左平行移动|h|个单位得到．

当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)^2 +k的图象；

当h>0,k<0时，将抛物线y=ax^2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

当h<0,k>0时，将抛物线向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)^2+k的图象；

当h<0,k<0时，将抛物线向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

因此，研究抛物线 y=ax^2+bx+c(a≠0)的图象，通过配方，将一般式化为y=a(x-h)^2+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．

2．抛物线y=ax^2+bx+c(a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是(-b/2a，[4ac-b^2]/4a)．

3．抛物线y=ax^2+bx+c(a≠0)，若a>0，当x ≤ -b/2a时，y随x的增大而减小；当x ≥ -b/2a时，y随x的增大而增大．若a<0，当x ≤ -b/2a时，y随x的增大而增大；当x ≥ -b/2a时，y随x的增大而减小．

4．抛物线y=ax^2+bx+c的图象与坐标轴的交点：

(1)图象与y轴一定相交，交点坐标为(0，c)；

(2)当△=b^2-4ac>0，图象与x轴交于两点A(x₁，0)和B(x₂，0)，其中的x1,x2是一元二次方程ax^2+bx+c=0

(a≠0)的两根．这两点间的距离AB=|x₂-x₁|

当△=0．图象与x轴只有一个交点；

当△<0．图象与x轴没有交点．当a>0时，图象落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图象落在x轴的下方，x为任何实数时，都有y<0．

5．抛物线y=ax^2+bx+c的最值：如果a>0(a<0)，则当x= -b/2a时，y最小(大)值=(4ac-b^2)/4a．

顶点的横坐标，是取得最值时的自变量值，顶点的纵坐标，是最值的取值．

词条图册

更多图册