商业中常见的许多连续变量的分布与正态分布非常相似。
正态分布可用于近似各种离散的概率分布。
由于正态分布与中心极限定理之间的关系,因此正态分布为其提供了经典统计推断的基础。
它是对称的,因此其均值和中位数相等。
外观为钟形。
其四分位数间距等于1.33标准偏差。
因此,中间值的50%包含在低于平均值的标准偏差的三分之二和高于平均值的标准偏差的三分之二的范围内。
它具有无限范围(-oo


升或更高,并且相等的数字预计少于1.025升。
符号f(X)用于表示概率密度函数。正态分布的概率密度函数在公式中给出。
e =用2.71828近似的数学常数
π=用3.14159近似的数学常数
μ =平均值
σ =标准偏差
X =连续变量的任何值,其中-∞
尽管公式看起来很复杂,但由于e和是数学常数,所以随机变量X的概率仅取决于正态分布的两个参数-平均值μ和标准偏差σ。每次指定μ和σ的特定值时,都会生成不同的正态概率分布。图说明了这一原理。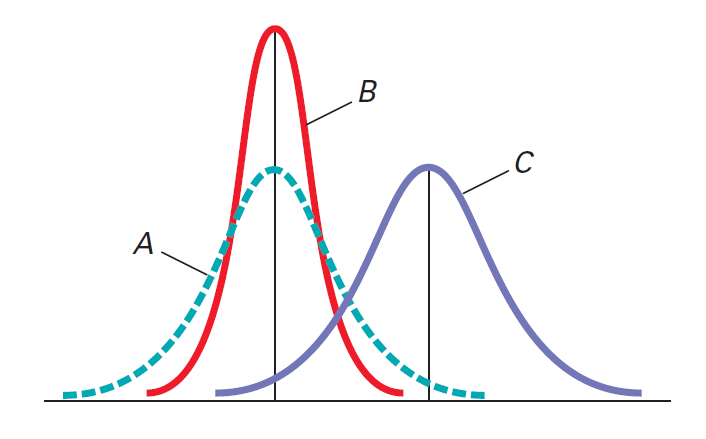
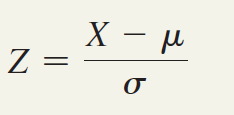
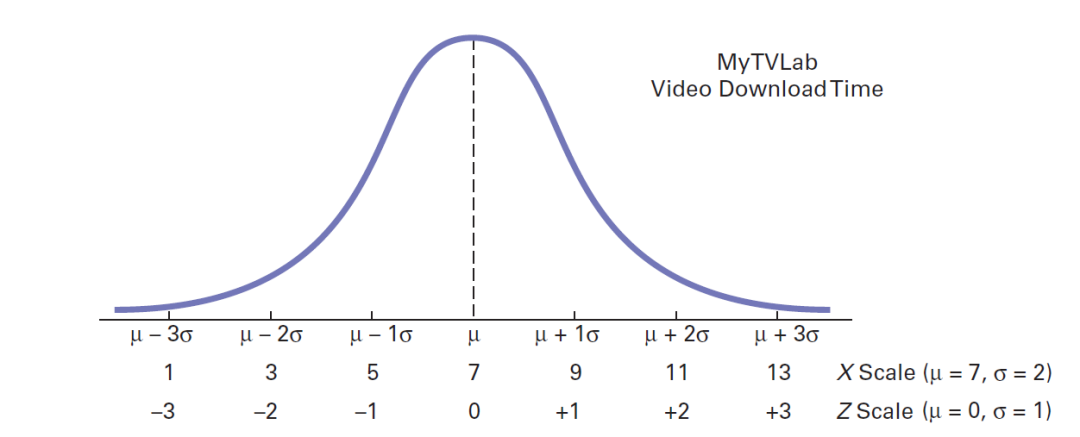
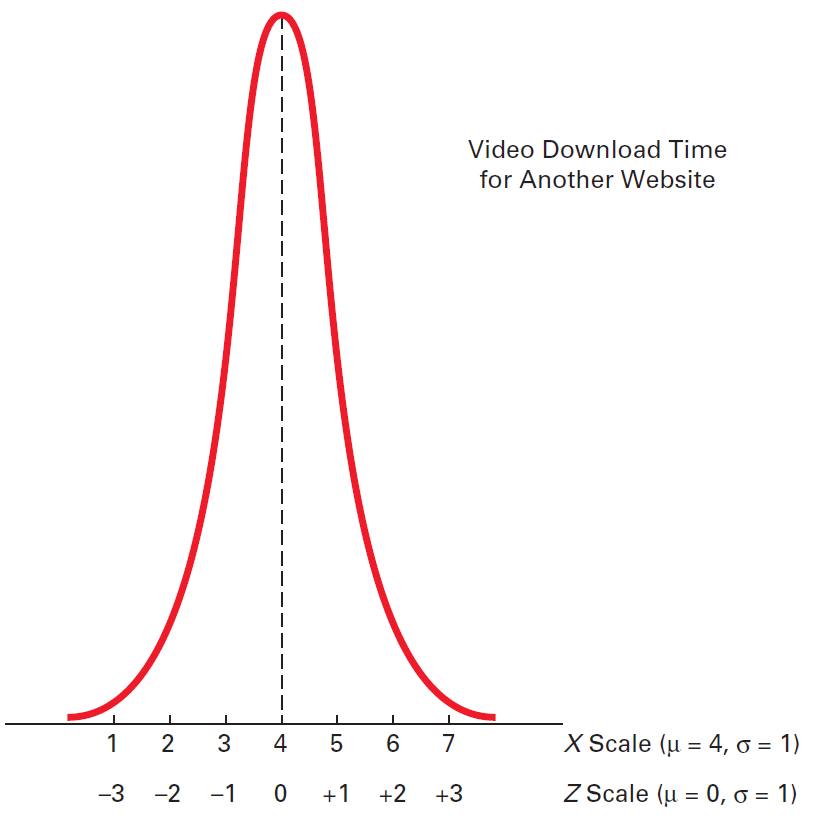
1秒的时间比平均下载时间低3个标准偏差,因为
Z = (1-4)/1= -3计算出Z值后,您可以使用累积标准化正态分布中的值表(查找正态概率。假设您想查找MyTVLab网站的下载时间少于9秒。假设平均u = 7秒,标准偏差σ = 2秒,则将X = 9转换为标准单位。导致Z值为+1.00使用此值,您可以使用表查找法线下的累积面积,该面积小于Z = +1.00(在其左侧)。要读取小于Z = +1.00的曲线下的概率或面积,请向下扫描表中的Z列,直到在1.0的Zrow中找到感兴趣的Z值(十分之一)。接下来,阅读该行,直到与包含Z值的第100位的列相交为止。因此,在表的主体中,Z = 1.00的概率对应于行Z = 1.0与列Z = .00的交集。下表显示了该交集。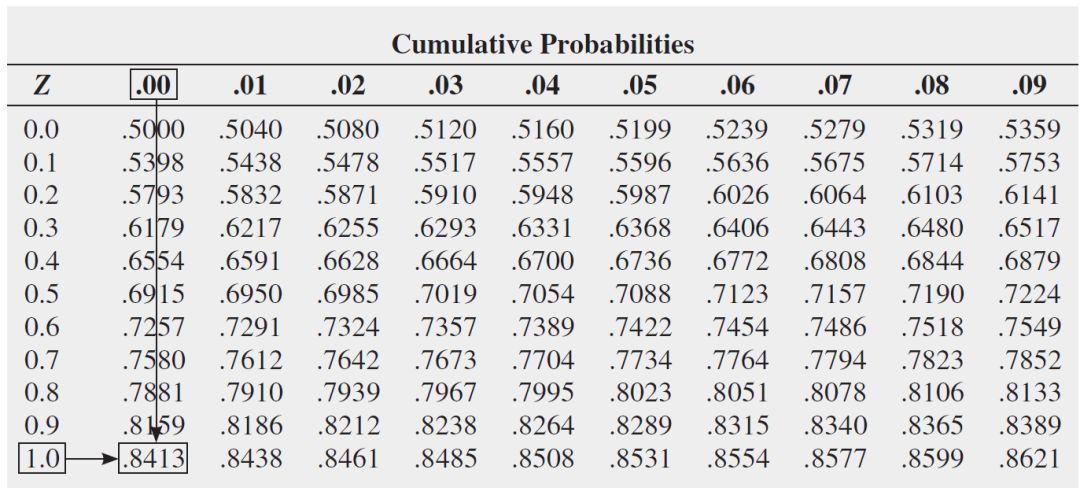
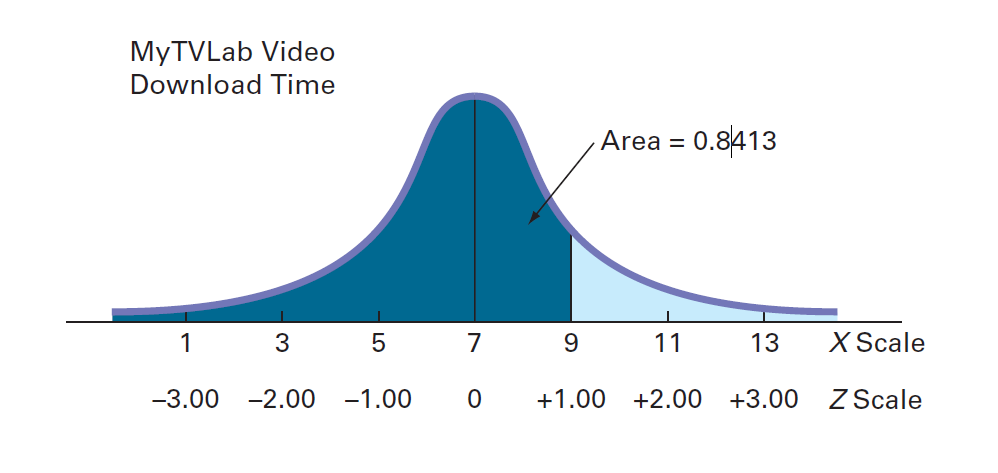
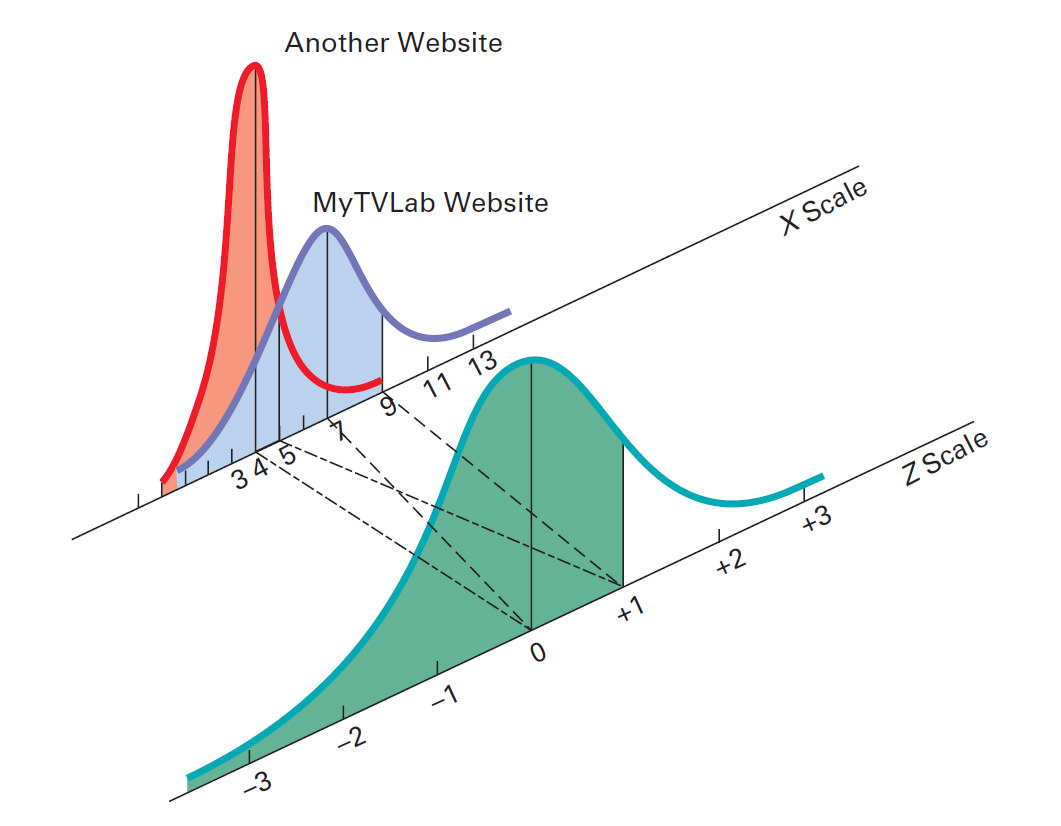
但是,对于其他网站,您看到5秒的时间比4秒的平均时间高1个标准化单位。因此,下载时间少于5秒的概率也为0.8413。下图显示,不管正态分布变量的均值u和标准偏差σ如何,公式(2)都可以将X值转换为Z值。
示例1
求P(X> 9)
MyTVLab网站的视频下载时间超过9秒的概率是多少?
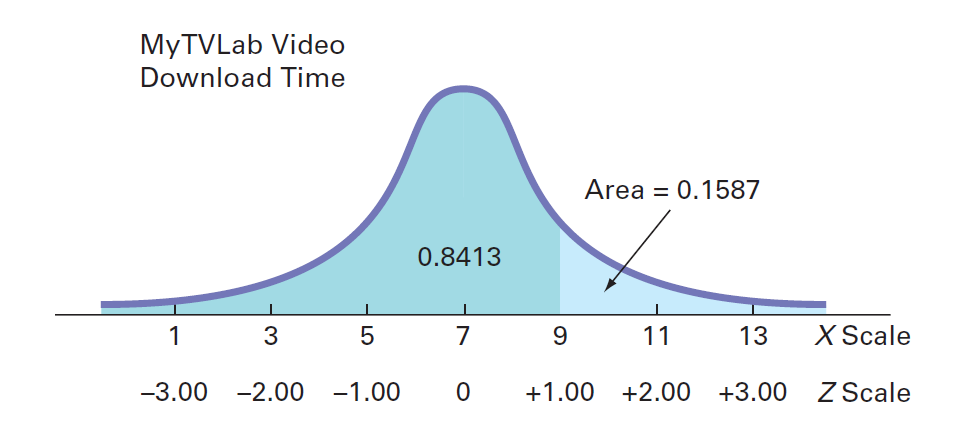
解:下载时间少于9秒的概率为0.8413。因此,下载时间将超过9秒的概率是1-0.8413 = 0.1587。下图说明了此结果。
例2,
求P(X <7 or X> 9)
MyTVLab网站的视频下载时间少于7秒或超过9秒的概率是多少?
解:要找到此概率,您可以分别计算下载时间小于7秒的概率和下载时间大于9秒的概率,然后将这两个概率相加。下图说明了此结果。
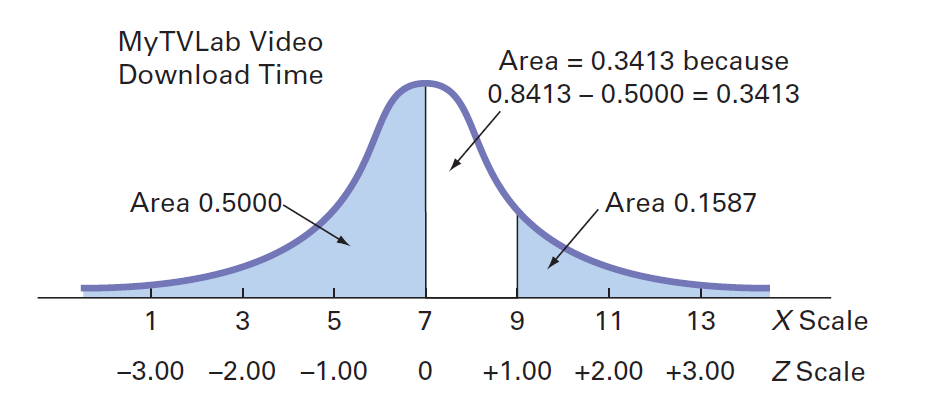
因为平均值是7秒,并且平均值等于正态分布中的中值,所以50%的下载时间在7秒以下。从例1中,您知道下载时间大于9秒的概率为0.1587。因此,下载时间低于7秒或超过9秒(P(X <7或X> 9))的概率为0.5000 + 0.1587 = 0.6587。
例3,
求P(5
MyTVLab网站的视频下载时间在5到9秒之间(即P(5
解:在下图中,您可以看到感兴趣的区域位于两个值5和9之间。
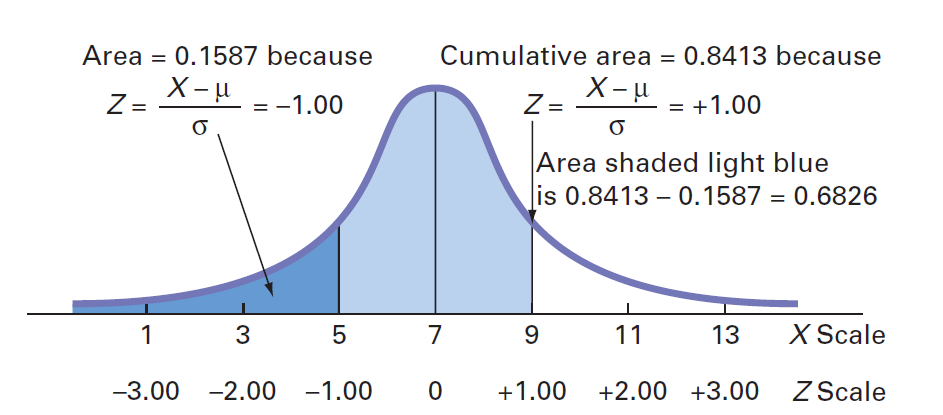
例3的结果使您可以声明,对于任何正态分布,这些值的68.26%将落在平均值的±1标准偏差之内。从下图中,您可以看到95.44%的值将落在平均值的±2标准偏差之内。因此,95.44%的下载时间在3到11秒之间。
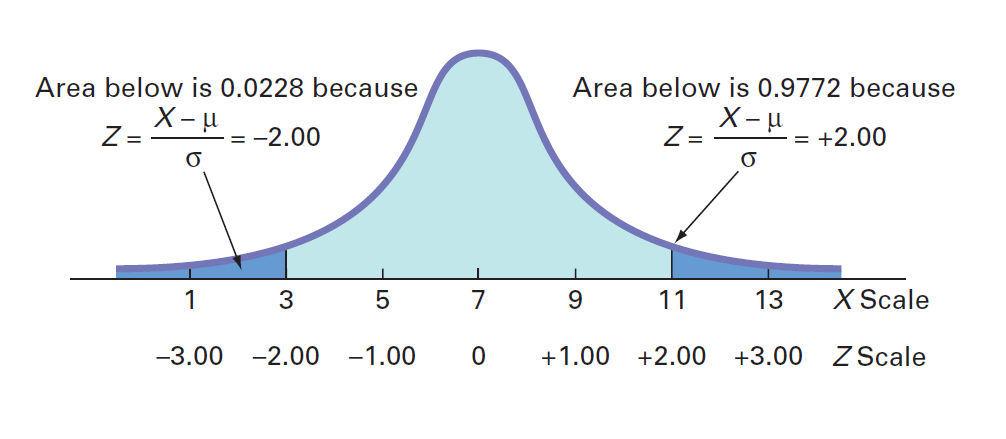
从下图中可以看到,该值的99.73%在平均值的上下3个标准偏差之内。
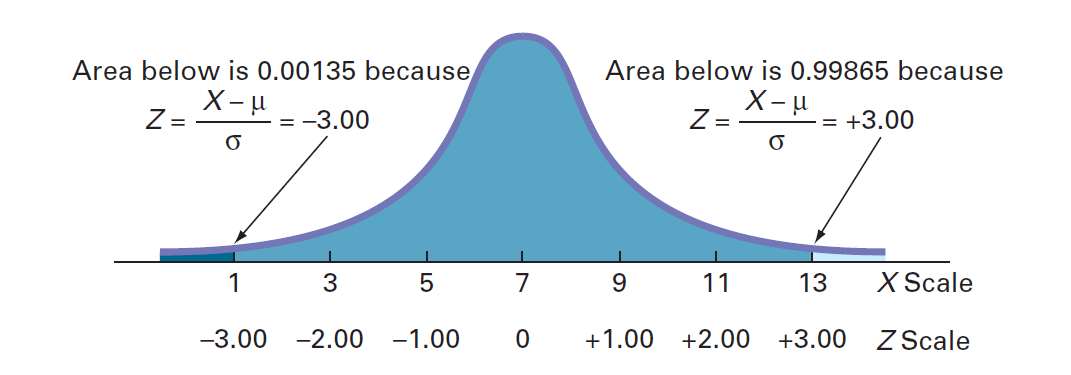
约68.26%的值落在平均值的±1标准偏差内
约95.44%的值落在平均值的±2标准偏差内
约99.73%的值落在平均值的±3标准偏差内
寻找X值示例1至3要求您使用正态分布表在正态曲线下查找与特定X值相对应的面积。对于其他情况,您可能需要执行相反的操作:查找对应于特定区域的X值。通常,您可以使用公式来查找X值。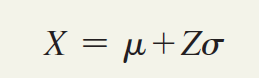
示例4
求出X值为0.10的累积概率。
MyTVLab视频的最快10%下载完成之前需要多少时间(以秒为单位)?
解:由于预计10%的视频将在X秒内下载,因此法线下小于该值的面积为0.1000。搜索面积或概率为0.1000。最接近的结果是0.1003,如表所示
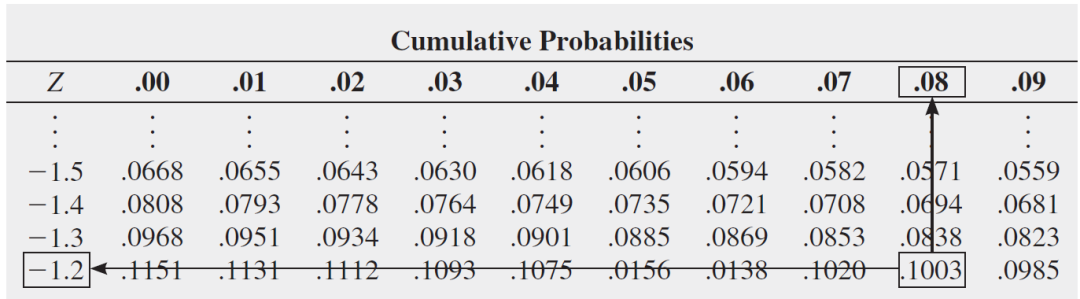
在正态分布线下找到对应于特定累积面积(0.10)的Z值
从该区域到表格的页边空白,您发现与特定的Z行(-1.2)和Z列(.08)相对应的Z值为1.28(见图)。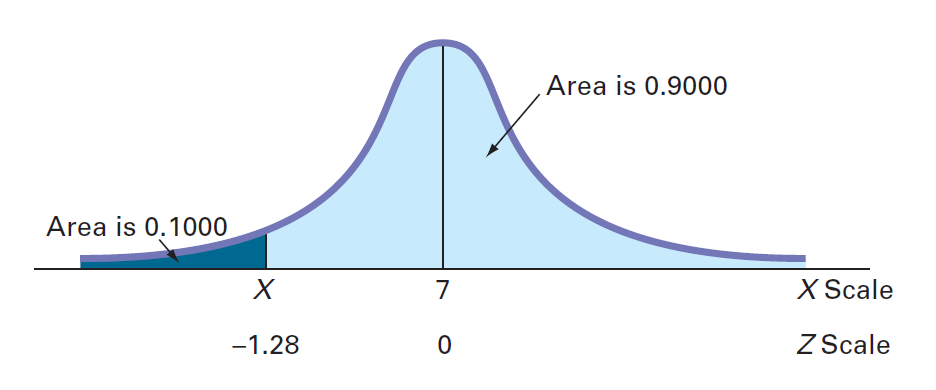
找到Z后,即可使用公式确定X值。
替换u = 7、σ= 2和Z = -1.28,
X = u + Zσ
X = 7 +(-1.28)(2)= 4.44秒
因此,下载时间的10%为4.44秒或更短。
例5,查找包含95%下载时间的X值。
围绕平均值对称分布的X的下限值和上限值是多少,包括MyTVLab网站上视频的95%的下载时间?解:首先,您需要找到X的较低值(称为XL)。然后,找到X的上限值(称为Xu),因为95%的值在XL和Xu之间,并且XL和XU与平均值均等距离,所以2.5%的值在XL之下(参见图)。
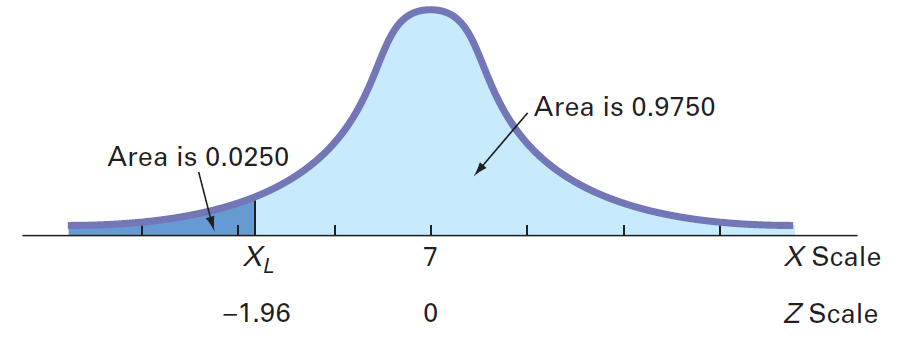
尽管X未知,但是您可以找到相应的Z值,因为曲线下的面积小于该Z的值为0.0250。使用表搜索概率0.0250。
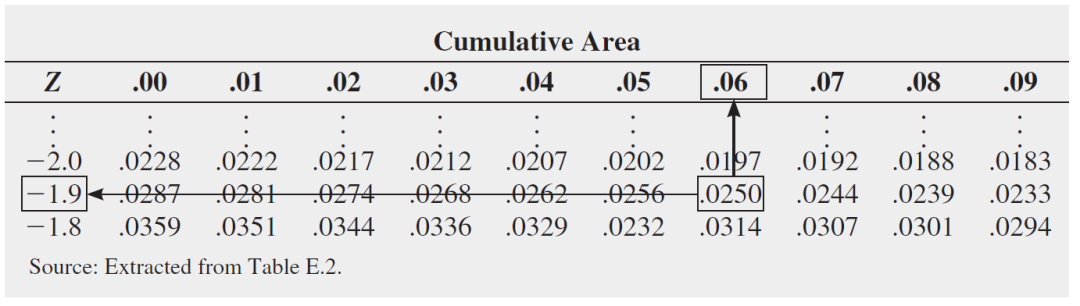
找到Z后,最后一步是使用公式,如下所示:
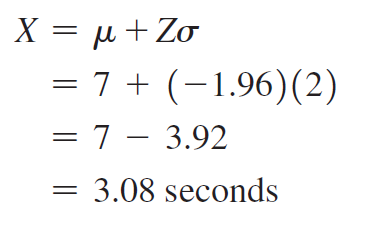
您使用类似的过程来查找X。由于仅2.5%的视频下载时间长于Xu秒,因此97.5%的视频下载时间短于Xu秒。从正态分布的对称性中,您会发现所需的Z值(如图所示)为+1.96(因为Z位于标准化均值0的右侧)。您还可以从表中提取此Z值。您可以看到曲线下的面积小于Z值+1.96,即为0.975。
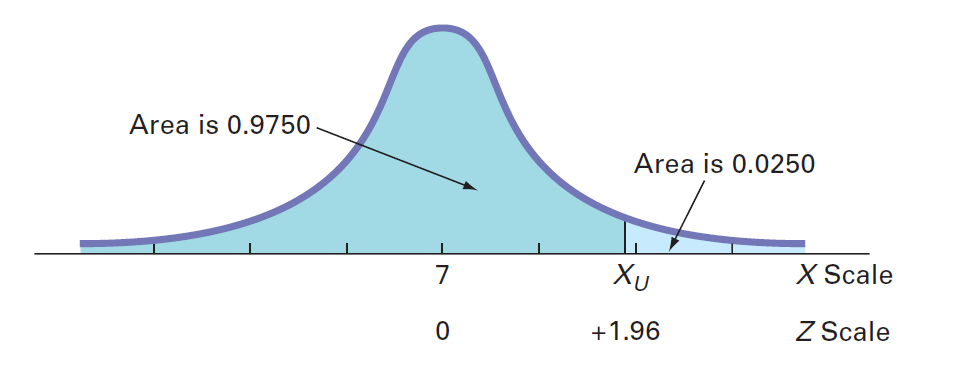
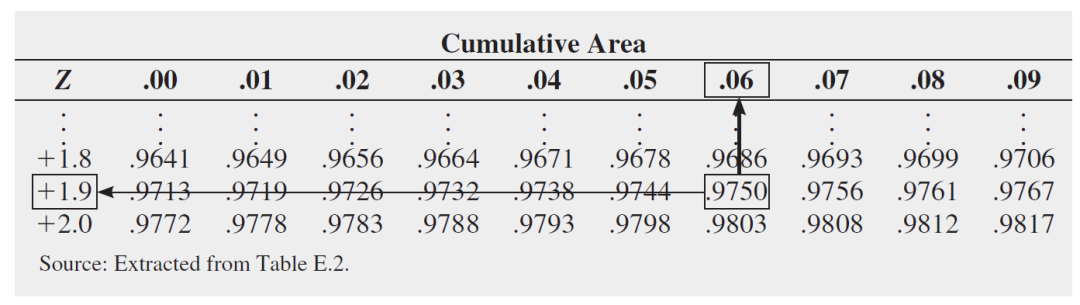
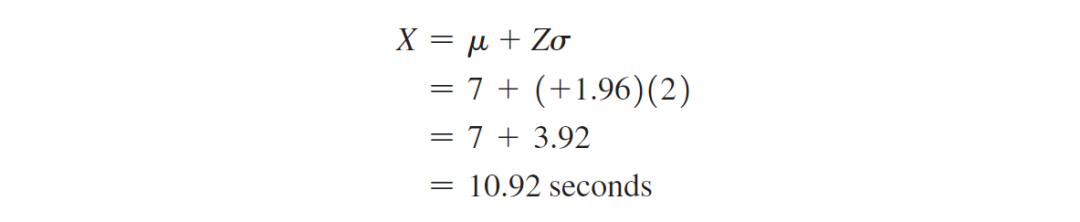
因此,95%的下载时间在3.08到10.92秒之间。
您可以使用Excel来计算1个正态概率,而不是在表中查找累积概率。图显示了一个工作表,该工作表计算正常概率并找到与示例1至5类似的问题的X值。
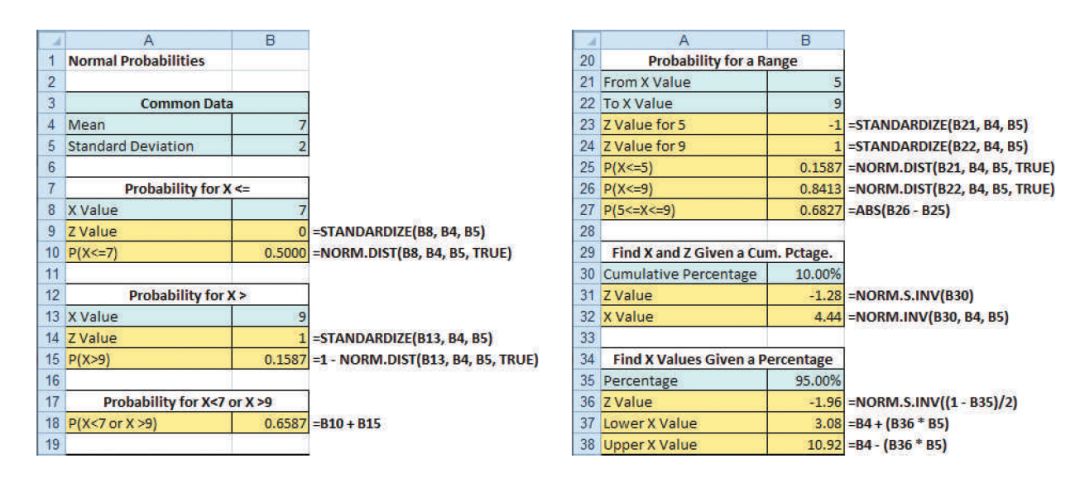
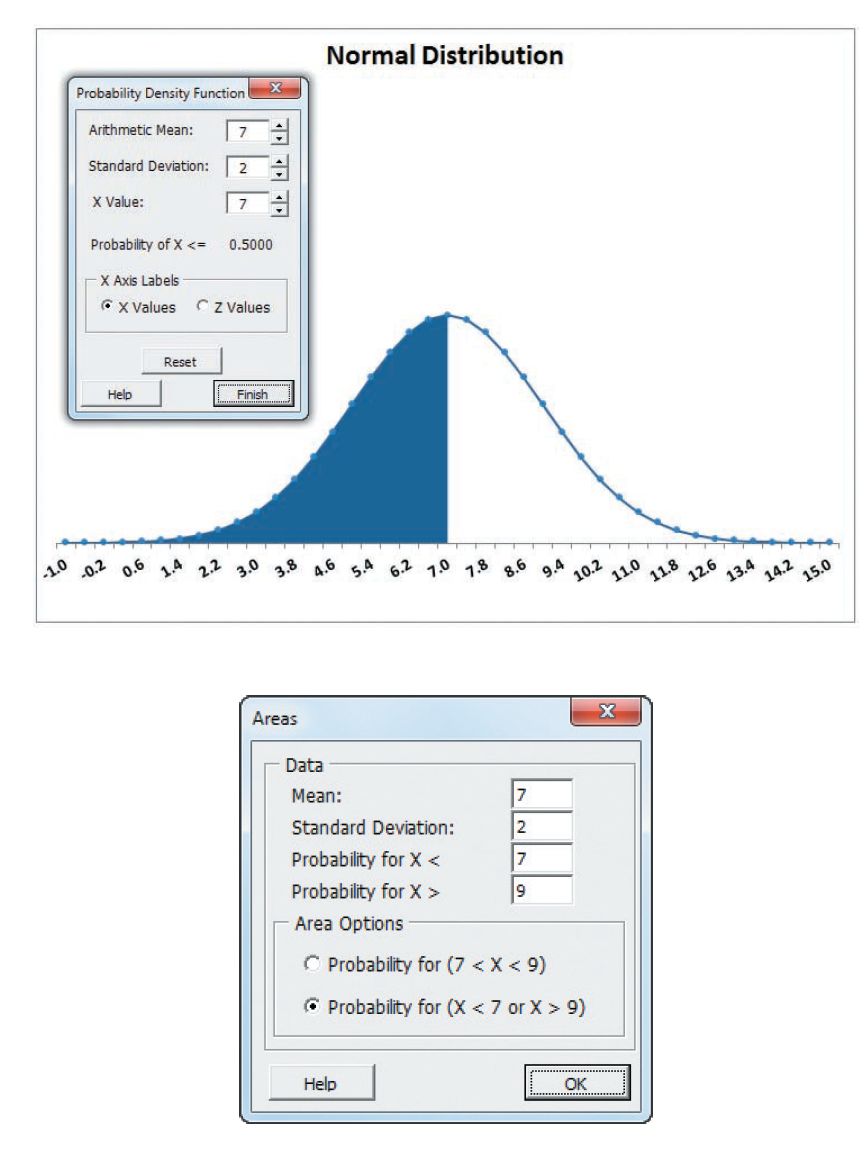




 本文介绍了正态分布的基本概念,包括其在商业中的应用和与中心极限定理的关系。通过示例展示了如何利用Excel的概率密度函数计算正态分布概率,包括求解下载时间超过或低于特定值的概率,以及找到特定累积概率对应的X值。
本文介绍了正态分布的基本概念,包括其在商业中的应用和与中心极限定理的关系。通过示例展示了如何利用Excel的概率密度函数计算正态分布概率,包括求解下载时间超过或低于特定值的概率,以及找到特定累积概率对应的X值。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








