反余弦函数的导数_图解普林斯顿微积分(重制) 09：反函数和反三角函数

最新推荐文章于 2021-10-10 23:16:21 发布
最新推荐文章于 2021-10-10 23:16:21 发布
阅读量1.3k 收藏
点赞数
文章标签： 反余弦函数的导数
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_31146939/article/details/112772184
版权

这里也衷心感谢 @Mr.C 同学协助转成将此系列原文档中公式转成 LaTeX 格式. ✪提示: 如果文中数字/公式显示较大, 请点击右上角中"刷新"即可恢复正常

▌第10 章反函数和反三角函数▌10.1 导数和反函数第一章就回顾了反函数(Inverse function)的基本知识, 可以快速地再看下, 请点击[这里]. 现在讨论导数和反函数之间的两个联系.10.1.1 使用导数证明反函数存在如果一个可导函数 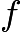53439522d5c60338c09ddee944c5ef5b.png , 它的导数总是正的, 那么该函数一定是递增函数, 且满足水平线检验. 没有水平线会与 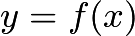a6186abd5d6e23c3f8e42cd8a0a34c1f.png 相交两次. 由于 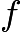53439522d5c60338c09ddee944c5ef5b.png 满足水平线检验, 所以我们知道 

最低0.47元/天 解锁文章
李昌刚
关注
  • 0
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
反余弦函数的导数_三角函数是如此重要，微积分十六个简单导数里它占了十个之多...
weixin_42300435的博客
01-16 3556
在数学、物理学和工程力学等诸多领域，矢量是很一个重要的概念。简单的去理解它，就是带方向的量，比如力F，速度v等都要作矢量分割。尤其在工程力学领域，两个不方向的量，其性质可能会有本质的区别。比如下图：这是一个对曲杆进行内力分析的微分单元。在这个微分单元的左侧，对于轴力N，其在切向上的分矢量N*sin θ/2，和剪切力Q的分矢量Q*cos θ/2构成剪切力的合力；而剪切力Q也一样，其在轴向上的分矢量Q...
二元函数对xy同时求导_关于反三角函数及其导数
weixin_39624873的博客
11-20 1210
反三角函数是基本初等函数的重要组成部分，但似乎又是许多人常问的主体之一。为了方便理解和查询，本文总结了以下内容：常见的六种三角函数对应的反三角函数的定义、定义域、值域，并给出对应三角形图示汇总、对应图象汇总利用反函数求导法则完成了上述所有反三角函数的导数公式的推导，并详细总结了其值域、定义域等内容本文内容也可作为备忘资料以便查阅使用。一、常用三角函数与反三角函数常见的六种三角函数可以分别由以下六种...
c++ 三角函数_常用三角函数公式备忘录（无证明）
weixin_42319865的博客
11-29 398
1.基本三角函数关系六边形规则。如图，每个顶点都是一个三角函数。1.1.对角乘积为1，如tanαcotα=1。1.2.任意一个顶点等于其相邻两个顶点的乘积，如sinα=tanαcosα。1.3.阴影处倒三角形上面两个顶点的平方和等于下顶点的平方，如tan²α+1=sec²α。2.一些特殊角的三角函数值 3.周期性与奇偶性 4.诱导公式 5.两角和差公式 6.和差化积、积化和差 7.二倍角...
反双曲函数
一个搬运知识的笨小孩
10-10 3万+
10.3 反双曲函数 反三角函数中的 ar 代表 arc（弧）【详见本人另一博客中 2.2 描述的三角函数的定义】 反双曲函数中的 ar 代表 area（面积）【详见本人另一博客中 9.7.0 描述的对双曲函数的定义】 双曲函数详见本人另一篇博客：https://blog.csdn.net/weixin_48524215/article/details/120614031 下图来自 Wikipedia 下图来自 Wikipedia 10.3.1 反双曲正弦函数【 y=arsinh(x) 】 y=sinh
逆函数求导公式_反函数求导公式,the formula about inverse-function's derivative,音标,读音,翻译,英文例句,英语词典...
weixin_39659748的博客
12-20 309
补充资料：反函数反函数inverse function反函数t~加“出佣;o6paT皿aa中，K”抓] 函数的完全逆象，即对给定函数值域的每个元素y都对应所给函数定义域的一切那样的元素的集合，使它们被映成y若用f表示给定的函数，则用f一‘表示f的反函数.这样，若f:X~Y且Yf为f的值域，玛CY，则对任意夕〔玛有厂’(y)一{‘:f(x)=y}· 若对一切y“Yf，夕的完全逆象恰由一个...
贝塞尔函数根分布及其导数.zip_bezier_导数_贝塞尔_贝塞尔函数 根_贝塞尔函数根
07-15
求第一类贝塞尔函数的根分布及其它的导数图形
AskBaseFunction_求B样条曲线的基函数导数_
10-03
本主题聚焦于如何计算B样条曲线的基函数及其导数，这对于理解和优化曲线形状至关重要。提供的两个MATLAB文件，`MyDersBasisFuns.m`和`MyBaseFun.m`，很可能是实现这一功能的源代码。 B样条（B-spline）是基于一组...
电脑计算器计算反函数共1页.pdf.zip
10-31
这些计算器通常提供高级数学运算，包括对数、指数、三角函数以及它们的逆函数，如arcsin（反正弦）、arccos（反余弦）和arctan（反正切）等。 标签“电脑计算器计算反函数共1页.pd”可能是文件的一部分路径或者错误...
反函数替换在微积分中的应用
06-03
里面内容包含了反函数替换在求极限、求导数、求积分等多个方面应用，读者看完对微积分必定产生一种新的认识。不管你是高手还是新手，绝对有茅塞顿开的感觉。 读者如果还不理解其中内容，欢迎找我进一步探讨问题！ 让...
2.3-反函数的导数-复合函数的求导法则.pdf
最新发布
11-17
在本节中，我们将讨论反函数的导数和复合函数的求导法则，这两个概念在微积分中非常重要。我们将从反函数的导数开始，接着讨论复合函数的求导法则，并提供一些例子来帮助读者更好地理解这些概念。 一、反函数的导数...
余弦函数导数推导过程_第十五讲 高阶导数
weixin_39915078的博客
11-23 2345
写在前面的话：本节内容是高阶导数(二阶及其以上的导数），为了便于大家理解我引入了“求导算子”的说法（这纯属个人说法，非官方）。另外有错误的地方还请指出，我及时纠正。小伙伴们一起学习吧~正文：二阶导数定义：如果函数 的导函数仍是 的函数，且导函数 是可导的，则 的导数称为原函数 的二阶导数，记作 或 或 即 或 。注：① 导函数 称为原函数 的一阶导数；② 求导算子 作为一个...
＜Zhuuu_ZZ＞HIVE(十一)函数
Zhuuu_ZZ的博客
09-22 2111
Hive内置函数一 Hive函数分类二 字符函数二 类型转换函数和数学函数三 日期函数四 集合函数五 条件函数六 聚合函数和表生成函数6.1 聚合函数6.2 表生成函数：输出可以作为表使用 一 Hive函数分类 从输入输出角度分类 标准函数：一行数据中的一列或多列为输入，结果为单一值 聚合函数：多行的零列到多列为输入，结果为单一值 表生成函数：零个或多个输入，结果为多列或多行 从实现方式分类 内置函数 自定义函数 UDF：自定义标准函数 UDAF：自定义聚合函数 UDTF：自定义表生成函数
正余弦函数及其反函数导数推导
TMS_LI的专栏
11-25 2万+
正余弦函数及其反函数导数推导背景三角函数的求导涉及到重要极限 limx→0sinxx\lim_{x\to0}\frac{sin x}{x} 的使用。 其反三角函数涉及复合函数求导。此文主要是对这两点知识的应用。三角函数求导sinxsin x(sinx)′=limdx→0sin(x+dx)−sin(x)dx (sin x)' = \lim_{dx\to0}\frac{sin(x+dx)-sin(
人工智能数学基础1：三角函数的定义、公式及固定角三角函数值
老猿Python
09-12 5769
☞ ░ 点此跳转到老猿Python博文目录░ 一、三角函数的定义及名称 在直角三角形中，当平面上的三点A、B、C的连线，AB、AC、BC，构成一个直角三角形，其中∠ACB为直角。对∠BAC而言，对边（opposite）a=BC、斜边（hypotenuse）c=AB、邻边（adjacent）b=AC，则存在以下关系： 二、三角函数的变化趋势及图像 正弦值在 [2kπ-π/2,2kπ+π/2]（k为实数，下同）随角度增大（减小）而增大（减小），在 [2kπ+π/2,2kπ+π*3/2] 随角度
余弦函数导数推导过程_反三角函数的导数的推导过程
weixin_40008033的博客
11-23 3253
反三角函数的导数的推导过程★根据反函数求导法则：反函数的导 数等于直接函数的倒 数。”先给出所有反三角函数的导数的总结：表1. 反三角函数的导数及其定义域接下来依次证明：1、反正弦函数 的导数2、反余弦函数 的导数证法I： 类似推导证法II：由，于是3、反正切函数 的导数4、反余切函数 的导数证法I：类似3，略。证法II： 类似2，由，于是5、反正割函数 的导数标 部分主要是要...
027 反三角函数的求导公式推导
段智华的博客
10-02 1万+
027 反三角函数的求导公式推导
反函数的求导法则
热门推荐
白水的博客
01-13 14万+
如果函数x=f(y)x = f(y)在区间IyI_y内单调、可导且f′(y)≠0f'(y) \neq 0，那么它的反函数y=f−1(x)y = f^{-1}(x)在区间Ix={x|x=f(y)，y∈Iy}I_x = \{x | x = f(y)，y \in I_y\}内也可导，且[f−1(x)]′=1f′(y)或dydx=1dxdy[f^{-1}(x)]' = \frac{1}{f'(y)} 或
反函数和反三角函数
一个搬运知识的笨小孩
10-10 9806
10.反函数和反三角函数 10.1 导数和反函数 10.1.1 使用导数证明反函数存在 如果满足水平线检验，则一个函数是否存在反函数 （一个 yyy 对应一个 xxx） 此方法的大体思想是：在一定区间内，如果函数单增或单减，函数图像必然与每条水平线只相交一次（即符合水平线检验），由此得出：存在该函数的反函数 10.1.2 用导数检验函数是否反函数：可能会出现问题 下面的分段函数满足 f′(x)≥0f'(x) \geq 0f′(x)≥0 ，符合水平线检验，不存在其反函数 问题： 导数为0的原函数表现为
常用导数公式
leemboy的博客
01-29 7227
In the following, u and v are functions of x, and n, e, a, and k are constants.   1. The Definition of the Derivative.         2. The derivative of a constant is zero.         3. The deriva

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值