matlab复化梯形公式求积分_7.3 复化求积法

由误差余项公式可知区间过大，误差亦大；为避免可选取适当多的节点，即选取相对高阶的Newton-cotes公式，但由稳定性分析又知：当阶数过大时，会出现不稳定的Runge现象。

复化求积法：将积分区间进行适当分段，在各分段子区间上采用低阶的Newton-Cotes求积公式，对各个小区间上的积分值进行一个近似，最后再累加起来。

例如：复化Simpson公式的推导：

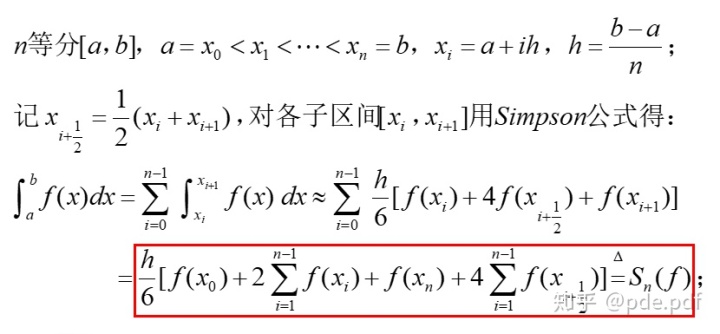
复化Simpson公式误差分析：

其中有个加一项减一项

区间逐次二分法

由复化求积公式的截断误差可知，加密节点可以提高求积公式的精度，但困难在于：使用公式之前需给出合适的步长，h过大，满足不了精度；h过小，计算量过大，因而实用的方法是采用区间逐次二分法，反复利用求积公式计算，直至二分前后两次积分值的差满足精度为止。

比如：对区间进行n等分，每个区间上先采用梯形公式，即复化梯形公式，若不能满足精度，则将每个小区间二等分，再分别采用梯形公式，不过端点处的值不用再算了，新算的只有新小区间上的二等分点处值，这样便可使计算量节约一半。

龙贝格算法（自动调整等分数）