求抛物线和直线交点_解读精炼22题 抛物线与直线的交点个数与参数取值范围 如何转化？...

H22.已知：二次函数y=x^2-4x+3a+2(a为常数)，(1)写出该二次函数图象的三个性质；(2)在同一坐标系中，若该二次函数的图象在x≤4的部分与一次函数y=2x-1 的图象有两个交点，求a的取值范围。

解读：

(1)图象的性质可以从开口方向、对称轴、顶点坐标、与坐标轴的交点、增减性等方面加以解读。

如图，该二次函数图象的开口向上，对称轴是直线x=2，当x≤2时，y随x的增大而减小，当x>2时，y随x的增大而增大；

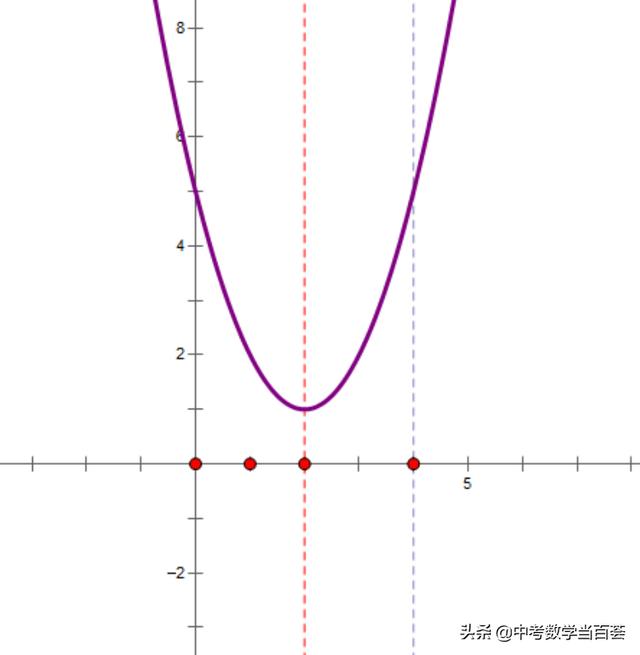
(2)二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点，如何解读？

可以从以下两个层面理解：

1.有交点的条件：联立解析式，得方程组，讨论方程根的情况，判别式>0

2.结合画图才能理解，x=4时，直线上的点为M(4,7)，抛物线上的点N(4,3a+2)，只有当点N在点M的上方或者重合时，抛物线在x≤4的部分与一次函数y=2x-1的图象才有两个交点，转化为不等式。

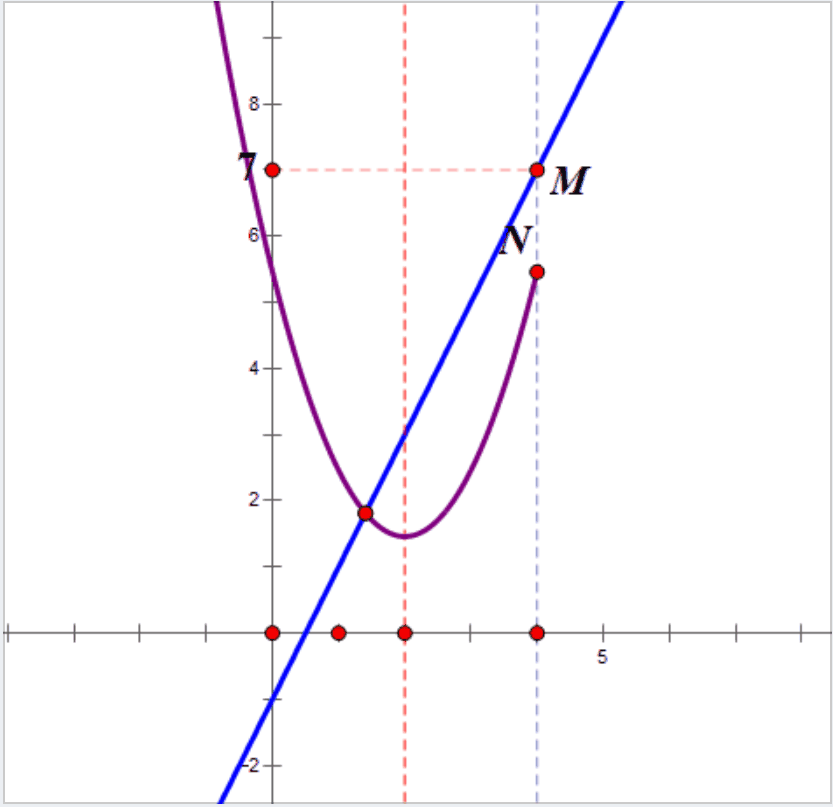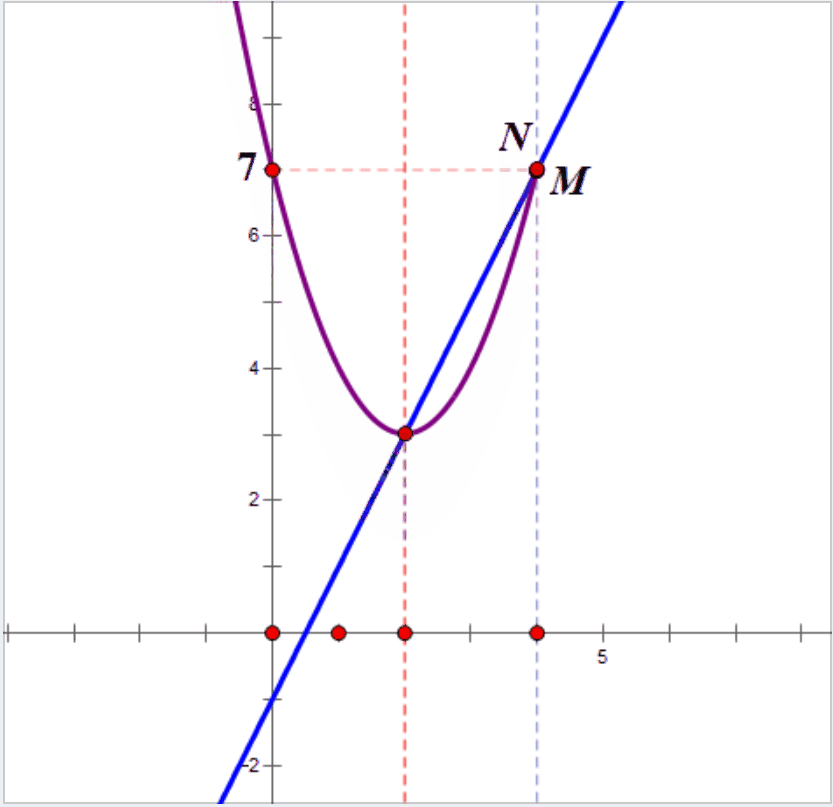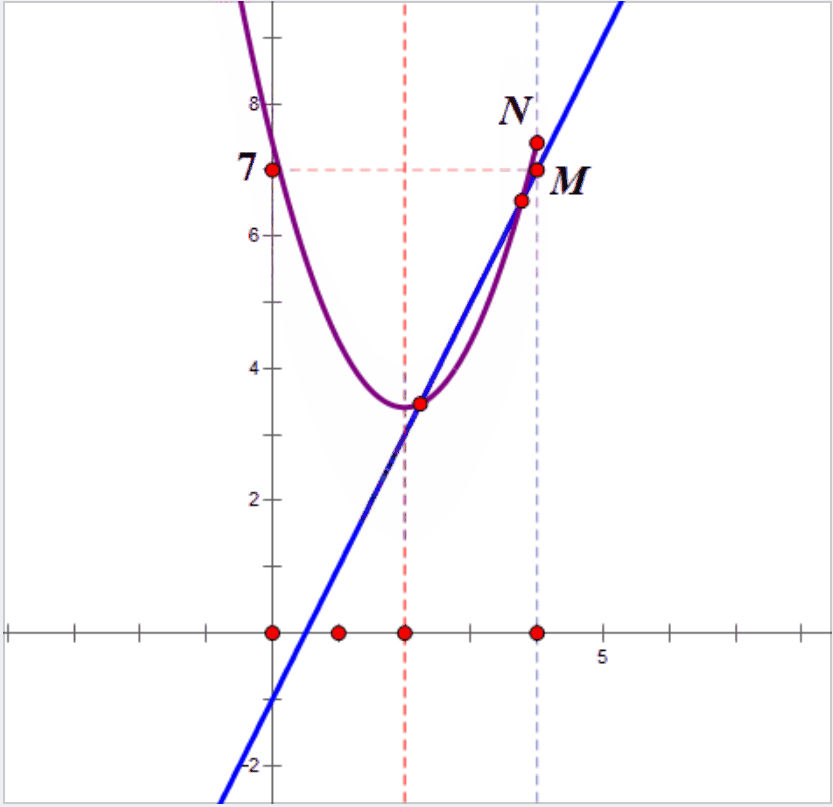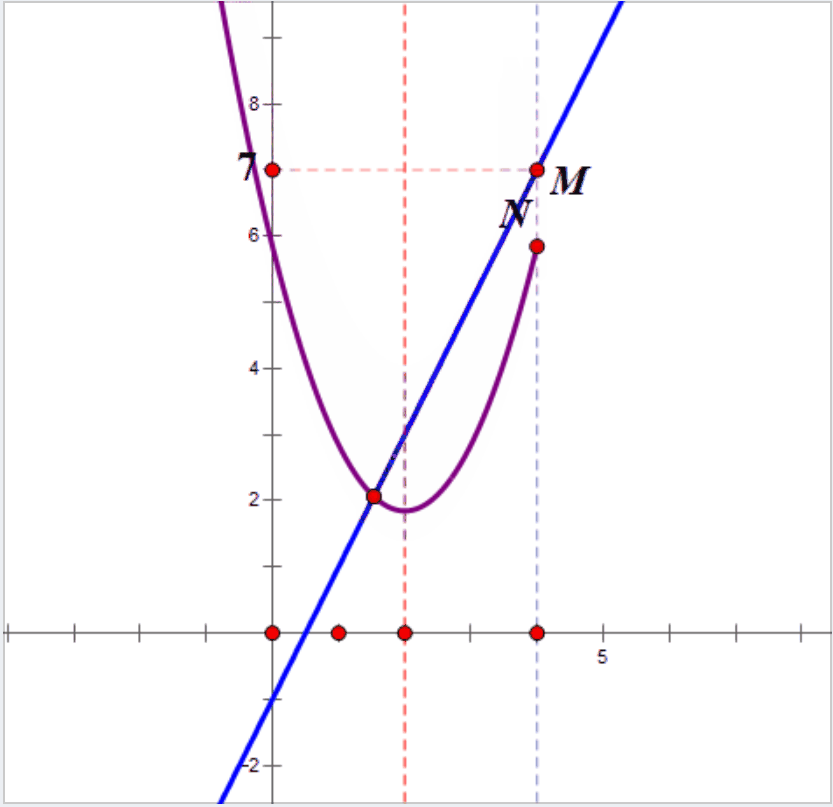
3.解不等式组，即可搞定a的范围。

联立y=x^2-4x+3a+2与y=2x-1

得x^2-6x+3a+3=0，

判别式△=24-12a，

因为抛物线(x≤4)与直线有两个交点，则

△=24-12a>0，解得a<2,

同时，当x=4时，直线上的点为M(4,7)，

抛物线上的点N(4,3a+2)，只有当点N

在点M的上方或者重合时，

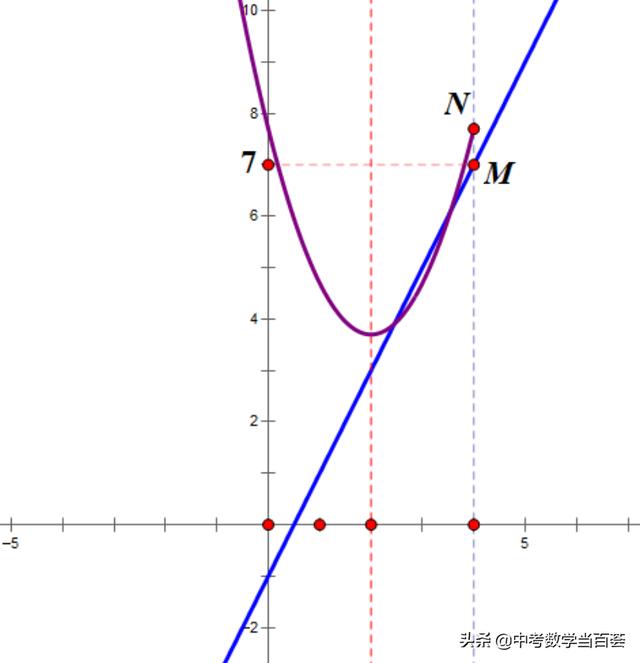
抛物线在x≤4的部分与一次函数y=2x-1的图象才有两个交点。

因而，3a+2≥7，解得a≥5/3

综合得：5/3≤a<2，即为所求。

---

今天战况如何？明天继续出题！