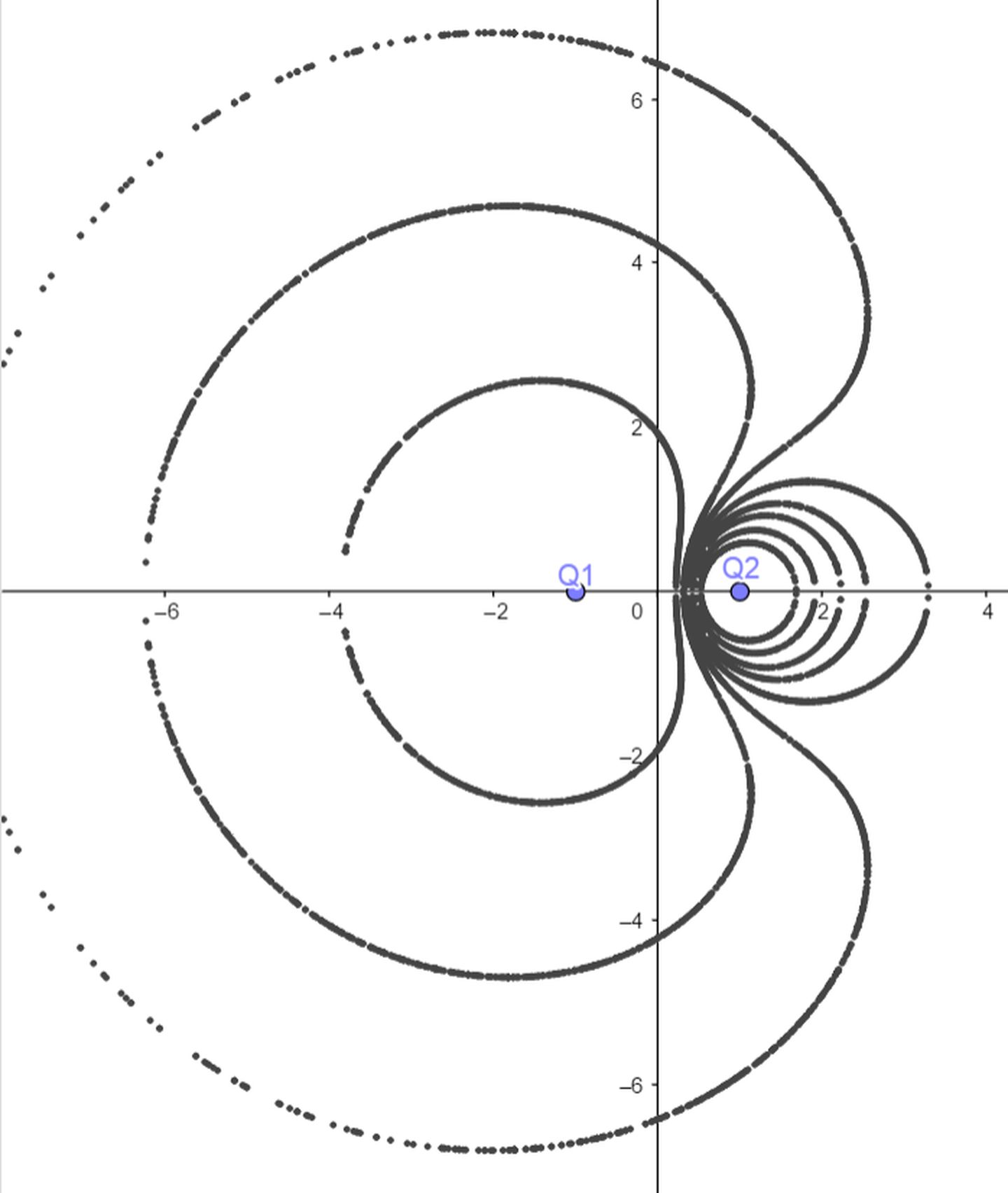
提要:本文介绍一种两点电荷等势线的几何作图法。
概述
平面上两点电荷的等势线是指平面上两点电荷产生的电势场的电势等值线。这两个电荷可以是相同电性的,也可以是相反电性的;可以是等量的,也可以是不等量的。如果两电荷间距为
如果
另外,应用这种方法,还可以直接作出零势圆(零势圆的定义后文会给出)。
作图原理
两点电荷的电势场为
为了作图方便,定义一个量
即
为了画出等势线,必须先找出
注意到如果将
下面先以等量同种电荷为例。即
现将直线
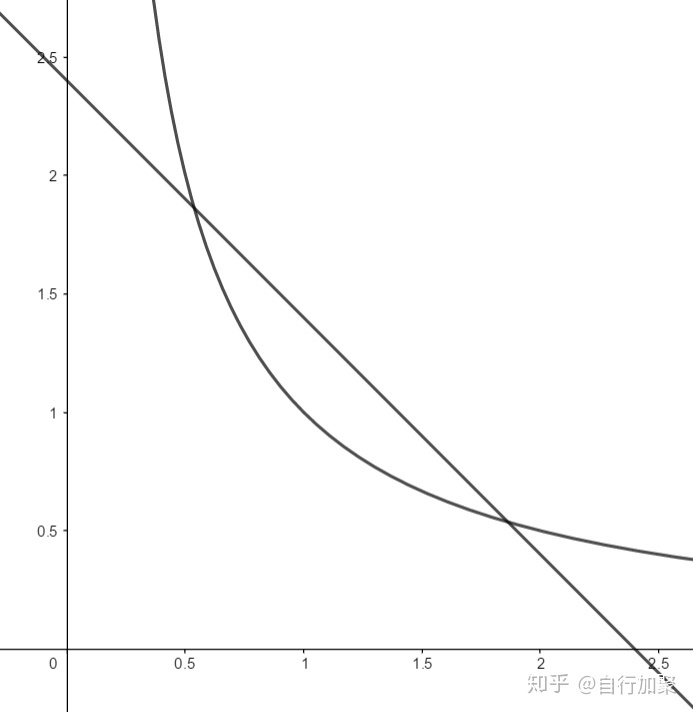
直接找双曲线上的点是没有意义的,因为满足条件的
于是在直线

显然,
过
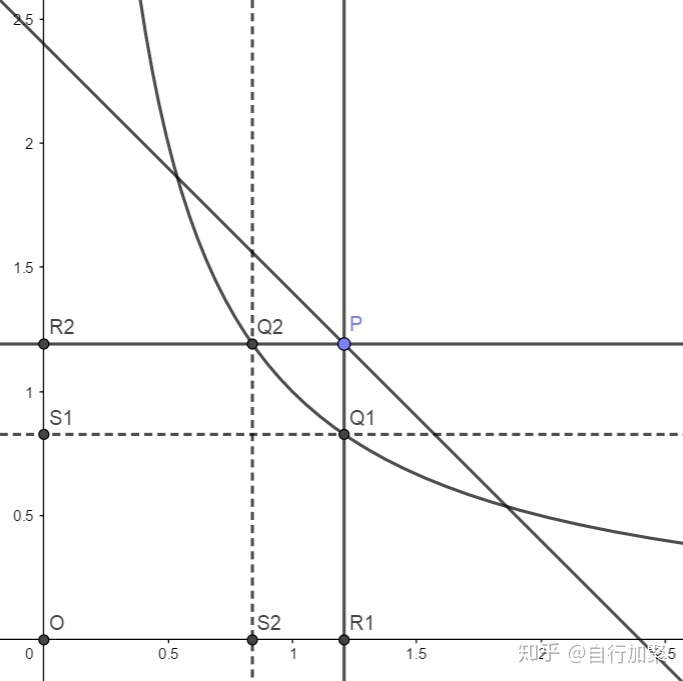
易知四边形
根据双曲线
所以
又因为
所以
即
这就找到了等势线对应的
现在的问题在于如何将这个两个线段长度转化为一个确定的点的位置。
现在另外一个平面上找两点
现在的目标是找到点
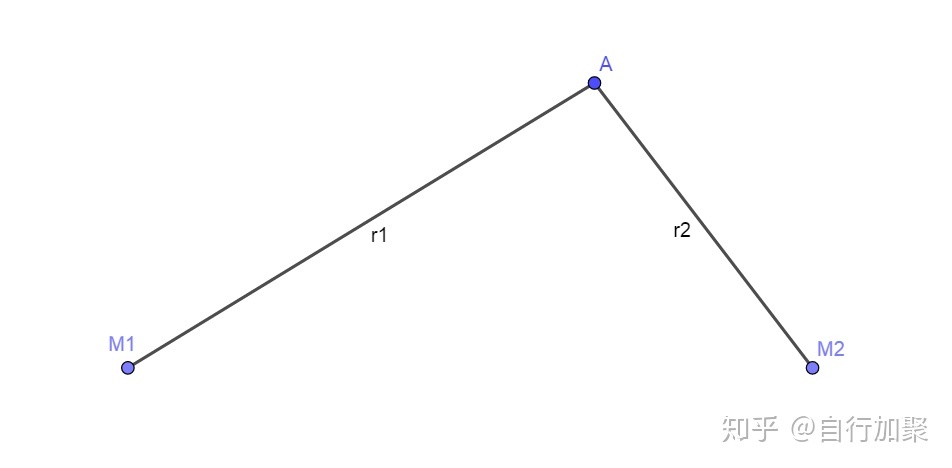
要
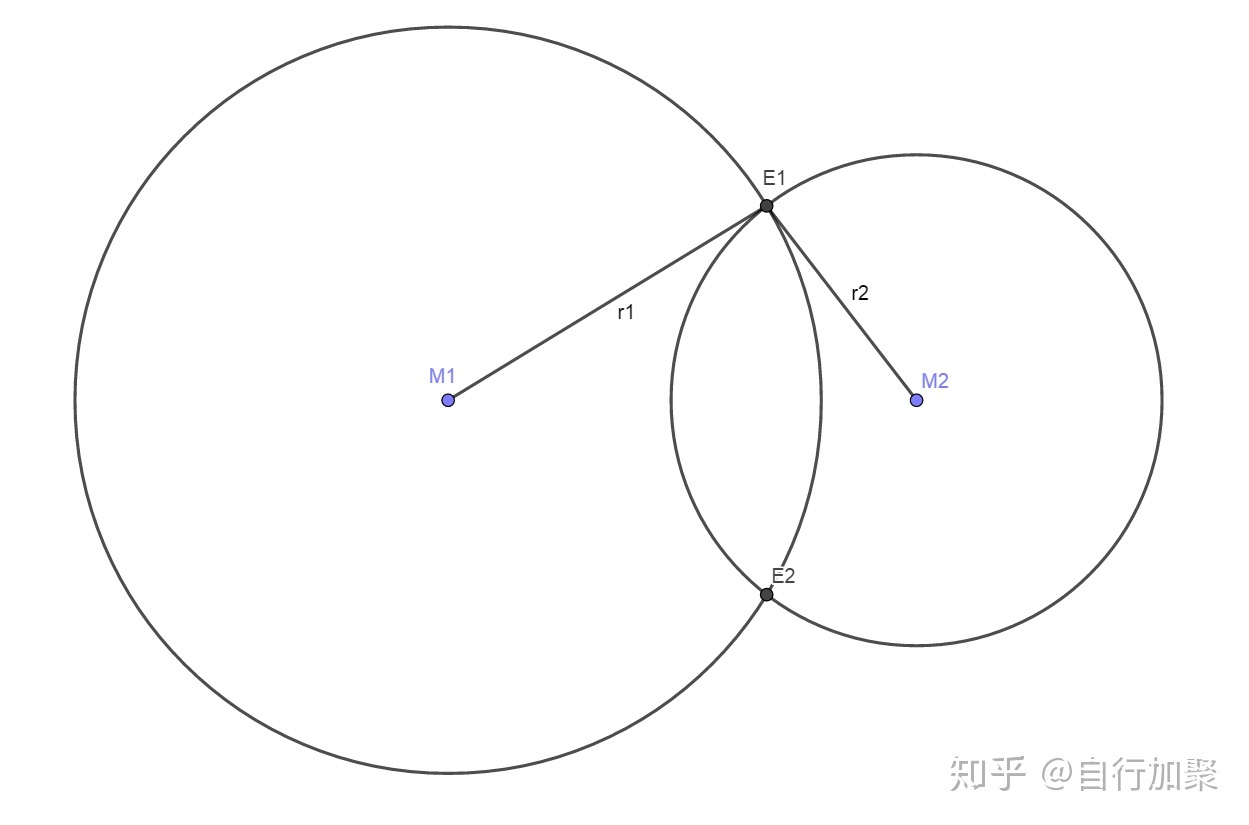
解毕。
当
下面用GeoGebra画图:
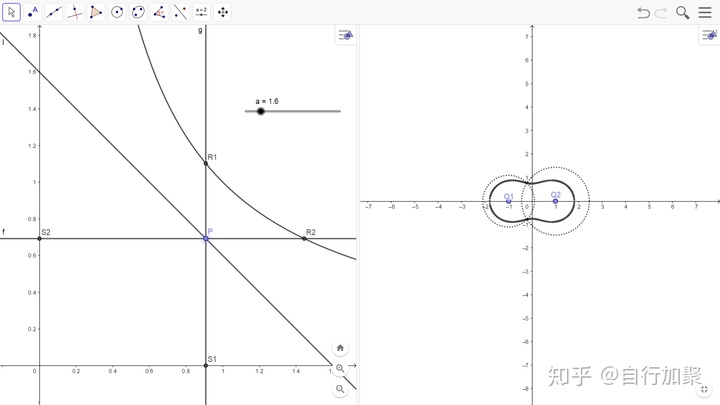
...以及更多的例子:
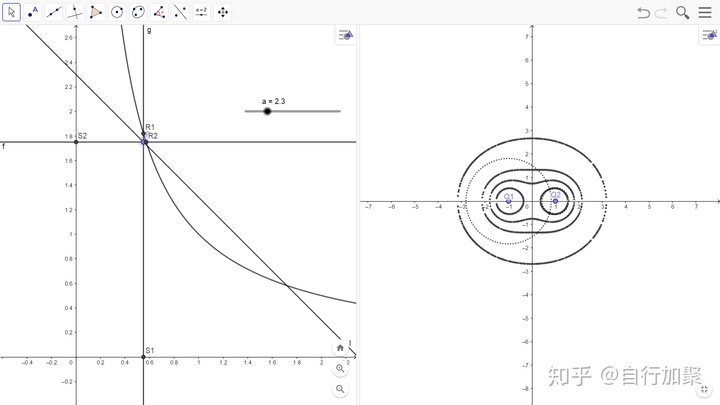
多漂亮!
在画图的时候,注意到如果
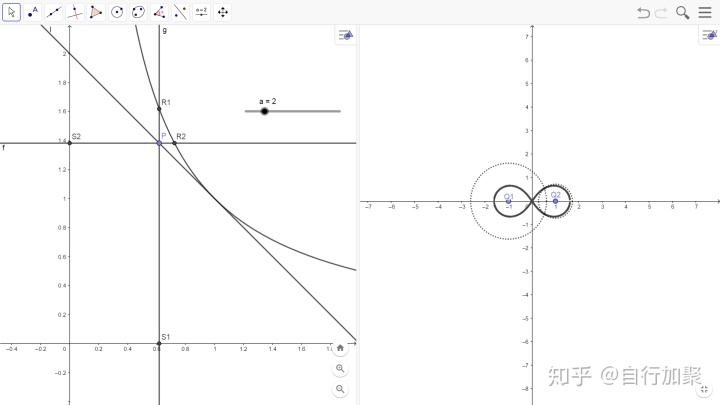
这是因为直线
即使得
所以此时
所以当
换言之,鞍点对应的
以上就是关于等量同种电荷等势线作法的说明。
了解了这种作法的核心思想,要知道其他情况(等量异种,不等量同种/异种)的作法就很简单了。
事实上,这个作法的结果完全取决于直线
下面再具体地稍作说明。
取直线
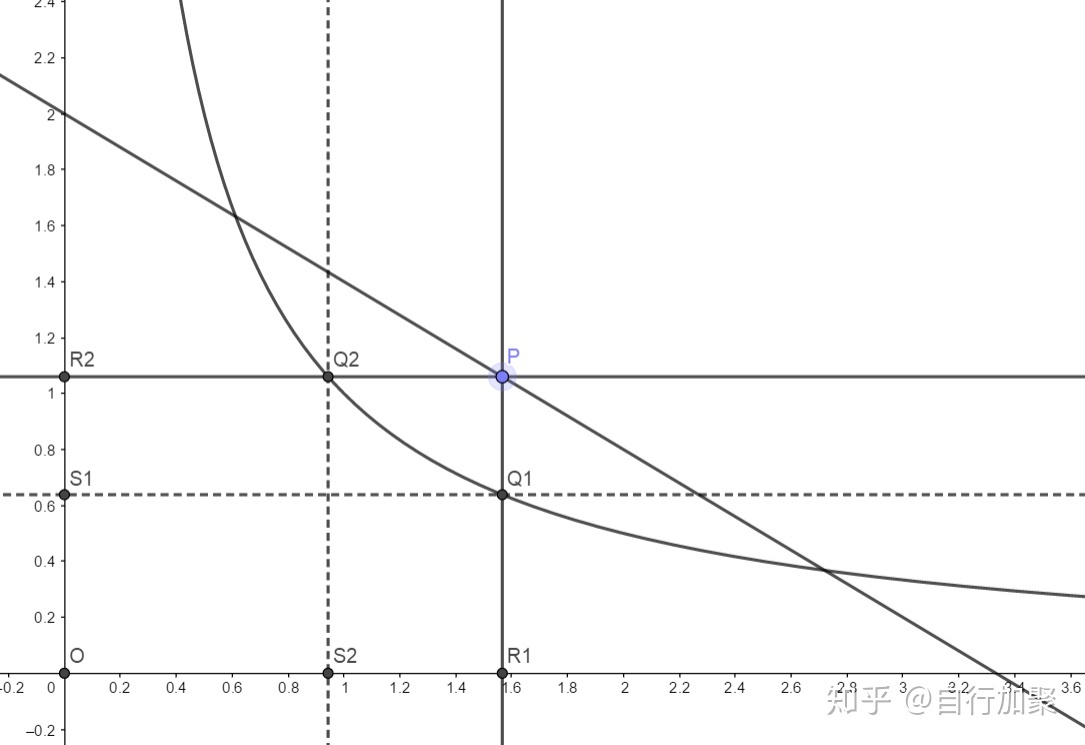
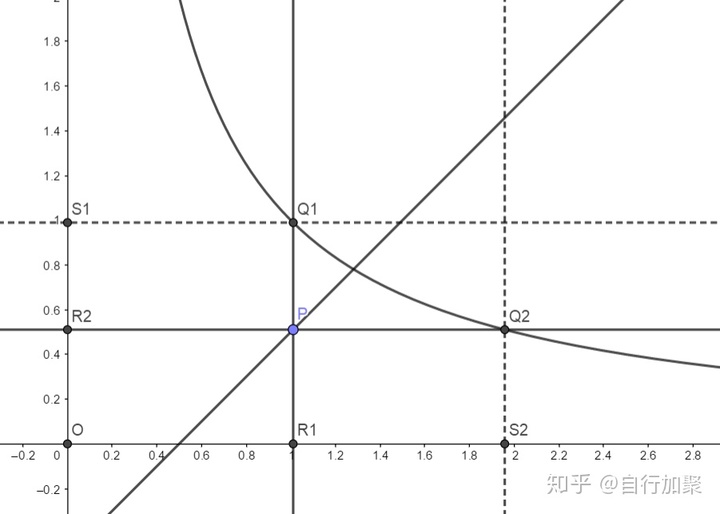
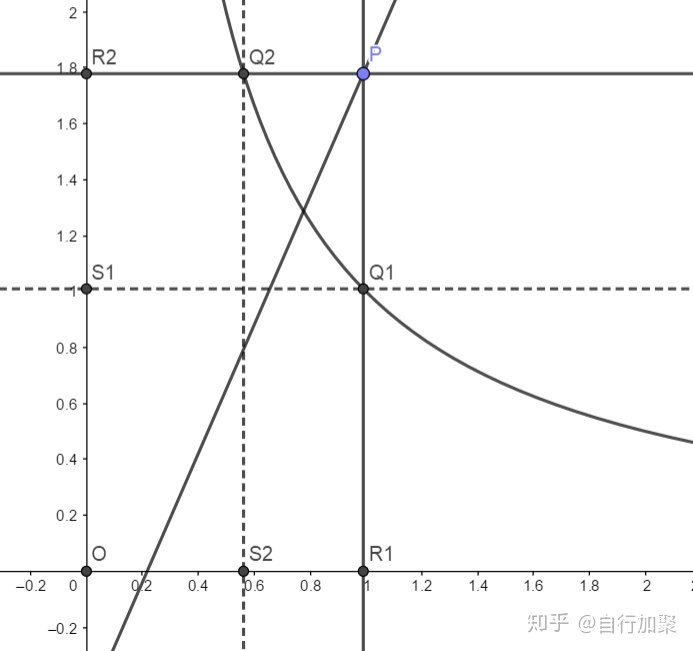
不难发现,无论是哪种情况,仍然满足关系:
- 当
即
时,为不等量同种,左侧电荷量大;
- 当
即
时,为等量同种;
- 当
即
时,为不等量同种,右侧电荷量大;
- 当
即
时,退化为单点电荷;
- 当
即
时,为不等量异种,右侧电荷量大;
- 当
即
时,为等量异种;
- 当
即
时,为不等量异种,左侧电荷量大;
- 其余情况不存在。
以上就是对这种等势线作法的说明。这一节的最后,附上几种情况的作图结果:
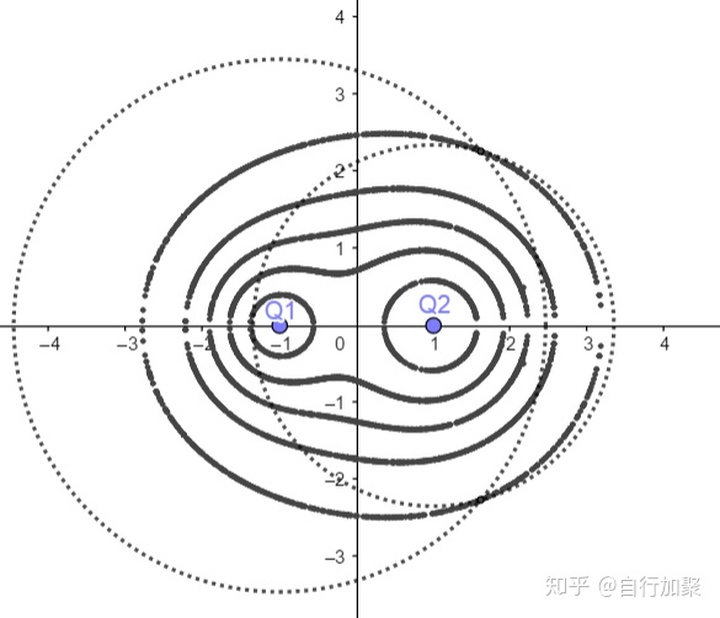
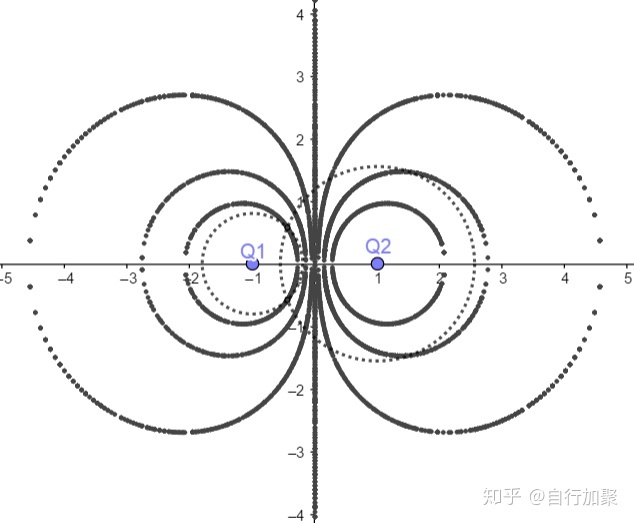
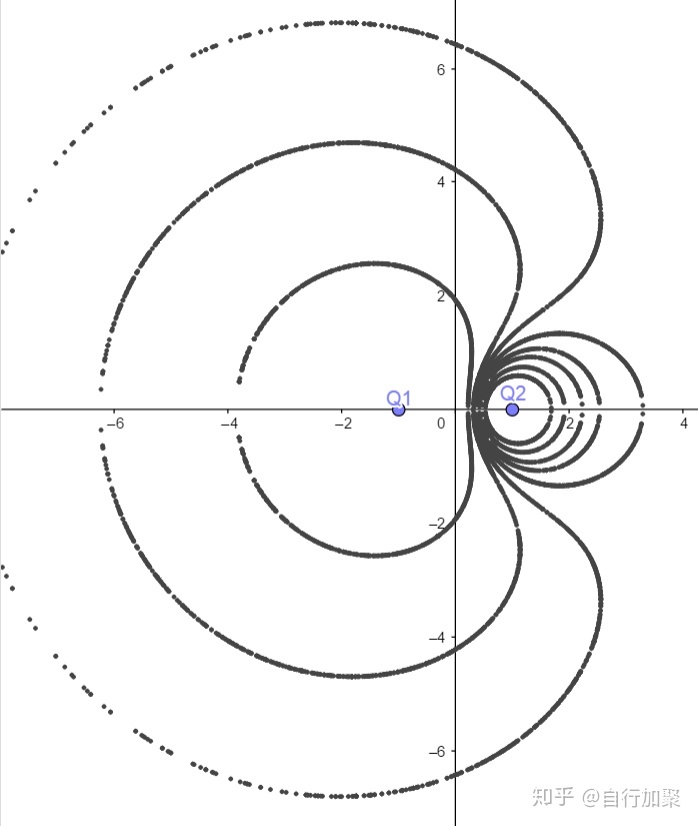
最后是作者的手稿:
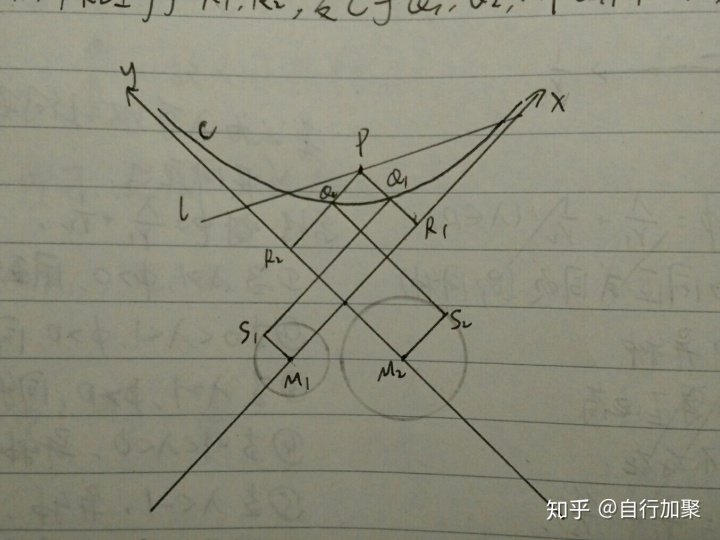
当然,我相信手画是可行的。
零势圆
这是我取的名字。
定理:在平面上异种电荷产生的电势场电势为0的等势线为一个圆,这个圆叫做零势圆。
需要注意的是,这里提到的圆是一个“广义的”圆,半径可以为无穷大。换言之,它可以是一条直线(这种情况在等量异种电荷中出现)。
当然,这只是等势线的一个特殊情况。将这个情况提取出来,是为了以此同解析几何方法作一个对比。至于孰好孰坏,由读者来评判。
好的,下面证明这个定理。
由几何关系易得,平面上异种电荷产生的电势场为:
(这里
按照定义有
移项得
两边同乘
两边平方得
展开得
整理得
整理到这里依然还是普适的,但要整理成圆的标准方程,要求
①
可以看出就是点电荷连线的中垂线。
②
显然是圆的标准方程。
证毕。
根据方程的性质,得到:
参考公式:
对于圆的标准方程![]()
![]()
圆心为![]()
半径为![]()
圆心在
半径为
即
作出这个圆并不困难,但是我们仍然可以利用关系
以相同的方法找两个圆的交点轨迹得到零势圆。
取直线
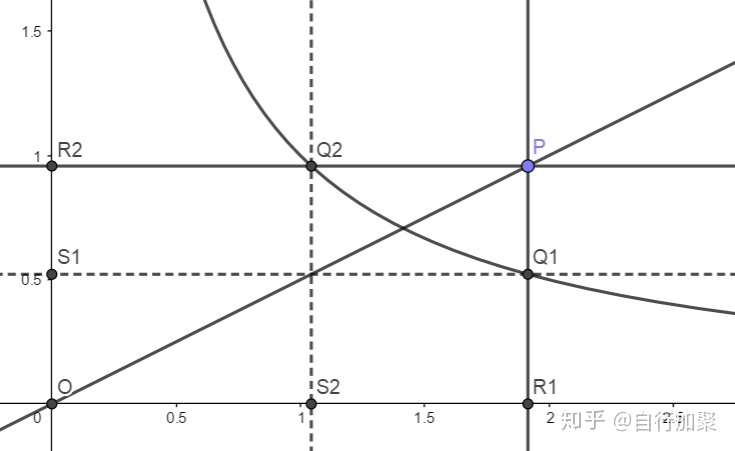
拖动
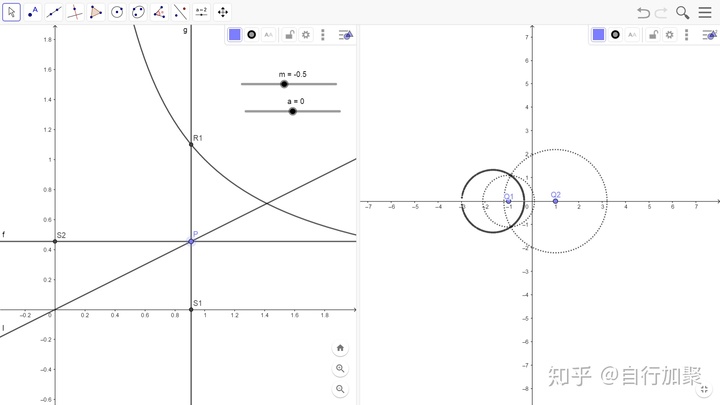
这看起来确实是一个圆,可惜这没有解答为什么这是一个圆。我相信这背后一定有一个漂亮的几何证明,但是我才疏学浅,未能得到。希望有心人能够补充证明。
以上介绍了平面内两点电荷的等势线的几何作法。
这个方法很可能是作者首创的,似乎前人没有发现这个作法。但如果不是,希望读者提出来。
以上。谢谢。







 本文提出了一种不借助解析几何的几何作图法,用于绘制两点电荷(同种或异种,等量或不等量)在平面上的等势线。详细阐述了作图原理,特别介绍了如何找零势圆,并通过GeoGebra展示了实例。文章还证明了异种电荷的零势线是一个圆,并提供了相关证明。
本文提出了一种不借助解析几何的几何作图法,用于绘制两点电荷(同种或异种,等量或不等量)在平面上的等势线。详细阐述了作图原理,特别介绍了如何找零势圆,并通过GeoGebra展示了实例。文章还证明了异种电荷的零势线是一个圆,并提供了相关证明。
















 1297
1297

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








