字节再融资
近期投行圈热度最高的事情,是字节跳动正在积极与相关金融机构展开洽谈,期望对其现有的 50 亿美元贷款进行再融资,期限三年。
若是再融资能成,大概率会成为中国借款人年内进行的最大规模贷款再融资交易事件。
这下可好了,一大波阴谋论出来了,有说字节跳动现金流断了,有说因为 TikTok 受美制裁,只能烧钱搞对抗...
真的入典 🤣🤣🤣
其实早在 2021 年,字节跳动就已经敲定了 50 亿美元的贷款,其中定期和循环信贷各占一半。
此次再融资更多的是为了降低融资成本、优化债务结构或满足其他财务需求,而非缺钱。
要知道字节跳动可是日均进账 20 亿人民币的超级独角兽。
到这里可能有网友会问,那字节这么有钱,为什么还要融资呢?
融资有诸多好处,其中一个比较好理解的优点,是风险控制。
例如有一个新业务要花钱,这时候首要考虑的,是项目失败后对公司的影响,而非该业务将来能够带来多少利润。此时一项较为常见的原则,是会去确保新业务所需资金来源的多元化,这样一定程度能够降低风险。每个独立项目都通过引入外部资金的方式来实现风险可控,也意味着公司相同的本金,能够支撑起更多的新业务。
贷款再融资,则可以理解为将用于「控制风险」的风险进一步降低。
贷款再融资可帮助实现债务重组(将多个高成本的短期债务转换为低成本的长期债务)、分散贷款(将单一机构贷款,分散给不同机构)和降低利率(将高利率贷款替换为低利率贷款)等等。
...
回归主题。
来一道和「字节跳动」相关的题目,也是经典的「手写数据结构」运用题。
题目描述
平台:LeetCode
题号:2558
给你一个整数数组 gifts,表示各堆礼物的数量。
每一秒,你需要执行以下操作:
-
选择礼物数量最多的那一堆。 -
如果不止一堆都符合礼物数量最多,从中选择任一堆即可。 -
选中的那一堆留下平方根数量的礼物(向下取整),取走其他的礼物。
返回在 k 秒后剩下的礼物数量。
示例 1:
输入:gifts = [25,64,9,4,100], k = 4
输出:29
解释:
按下述方式取走礼物:
- 在第一秒,选中最后一堆,剩下 10 个礼物。
- 接着第二秒选中第二堆礼物,剩下 8 个礼物。
- 然后选中第一堆礼物,剩下 5 个礼物。
- 最后,再次选中最后一堆礼物,剩下 3 个礼物。
最后剩下的礼物数量分别是 [5,8,9,4,3] ,所以,剩下礼物的总数量是 29 。
示例 2:
输入:gifts = [1,1,1,1], k = 4
输出:4
解释:
在本例中,不管选中哪一堆礼物,都必须剩下 1 个礼物。
也就是说,你无法获取任一堆中的礼物。
所以,剩下礼物的总数量是 4 。
提示:
基本思想
为了方便,将 gifts 记为 gs。
从题面看,数组大小和执行次数范围均为 ,那么暴力做法的复杂度为 ,计算量为 ,是可以通过的。
稍有数据结构基础的同学,容易进一步联想:存在一种数据结构,能够快速查得集合最值,使复杂度降低。
该数据结构是「堆」,在某些 STL 里面又称为「优先队列」。
手写堆入门
所有高级数据结构(例如之前讲过的 [字典树 Trie] 或 [并查集],都可以使用数组进行模拟,堆自然也不例外。
「堆本质是数据集合,只不过区别于简单数组而言,其具有 查找最值特性。」
既然我们使用数组来实现堆,同时又需要实现 查找最值,一个自然而然的想法,是把集合最值放到数组的特定位置,例如数组起始位置。
开始之前,先来了解一下,堆的基本操作:
-
add:往堆中增加元素 -
peek:快速查得最值 -
pop:将最值从堆中移除
我们以小根堆为例,进行学习。
❝PS. 大根堆亦是同理,如果已经有写好的小根堆模板,那么将数值进行符号翻转,即可实现大根堆;或是翻转模板中的数值比较逻辑,也可将小根堆轻松切换成大根堆。
❞
1. 堆长啥样?
堆是数组实现的,但其形态为「完全二叉树」(最多只有底下一层节点不满),目的是尽量让树平衡,降低树的高度,从而更高效的维护其性质。
虽是「完全二叉树」,但其又和另外一种特殊二叉树,二叉搜索树(BST)不同。
在 BST 的定义中:任意节点的左子树上的节点值均不大于该节点,任意节点的右子树上的节点值均不小于该节点。
在小根堆对应的「完全二叉树」定义中:任意节点的节点值均不大于其左右子树中的节点值。
因此将小根堆可视化后,也十分形象:小根堆的堆顶元素最小,然后从上往下,元素“依次”增大。
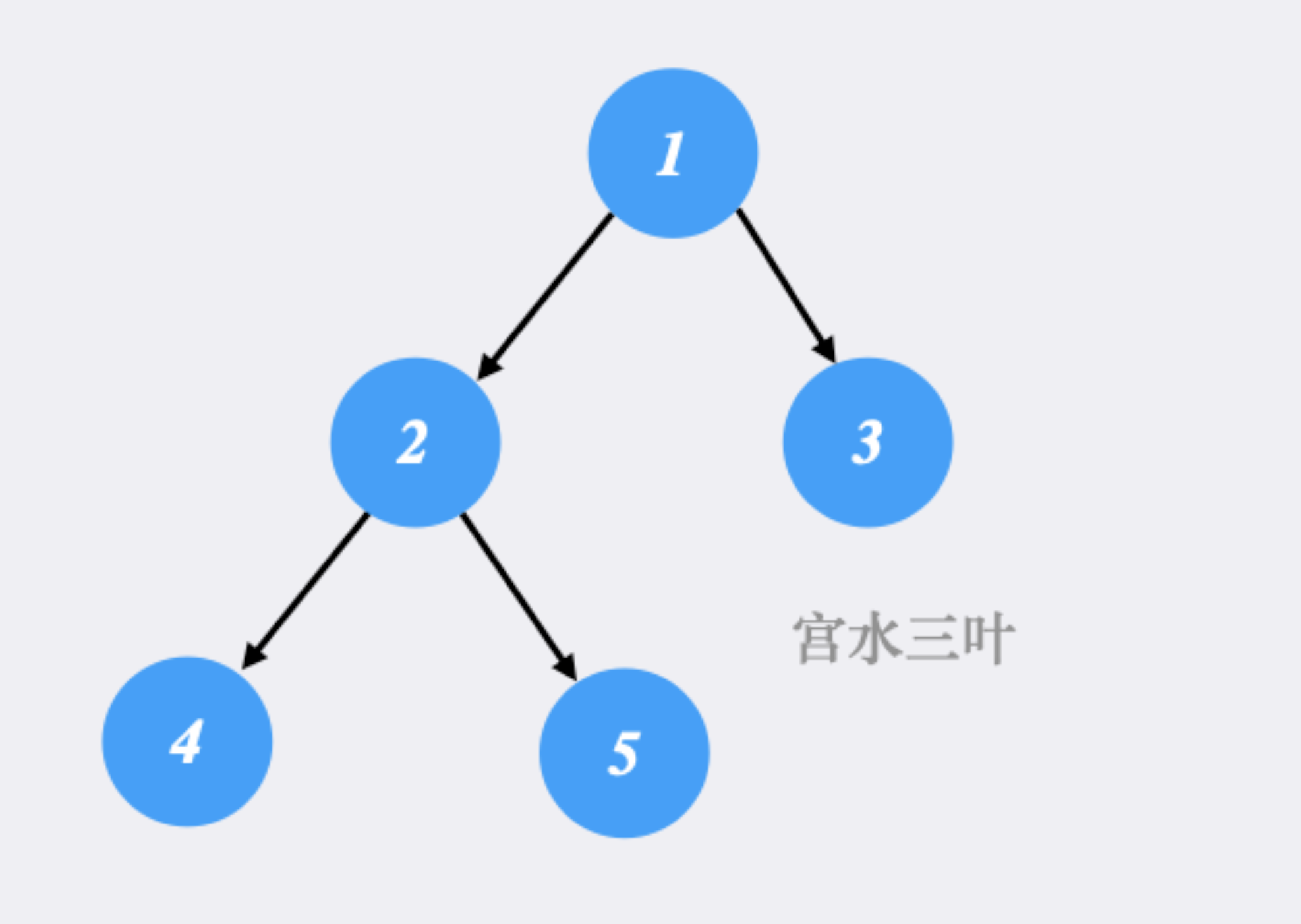
即对于小根堆而言,每个子树的根节点,都是该子树的最小值。
2. 如何用数组进行「完全二叉树」的存储?
我们只需要将「二叉树的左右子节点关系」和「数组下标」实现某种关联即可。
我们约定,对于某个节点,若其所在数组下标为 idx,那么该节点的左子节点的数组下标为
,该节点的右子节点的数组下标为
。
注意:基于此规则,我们需要调整数组下标从 1 开始进行存储。

3.基本操作如何实现?
所有操作的核心最终都归结到:如何通过有限的调整,重新恢复堆所对应的完全二叉树中的节点定义。
因此可抽象出 up 操作和 down 操作,俩操作均通过递归实现:
-
up操作是将当前节点u与父节点fa = u / 2进行比较,若发现父节点更大,则将两者进行互换,并递归处理父节点 -
down操作是将当前节点cur和左右节点l = cur * 2和r = cur * 2 + 1进行比较,若当前节点并非三者最小,则进行互换,并递归处理子节点
通过上述核心 up 和 down 操作,以及「完全二叉树」在数组的放置规则,我们可以容易拼凑出堆的基本操作。
假定当前使用一维数组 heap 实现堆,使用变量 sz 记录当前堆的元素个数,同时该变量充当 heap 的结尾游标:
-
add:往堆中增加元素 该操作可转换为:往数组尾部增加元素(heap[sz++] = x),并从尾部开始重整堆(up(sz)) -
peek:快速查得最小值 直接范围数组首位元素,注意下标从 开始,heap[1] -
pop:将最值从堆中移除 先通过peek操作记录下待移除的最小值,然后将数组的结尾元素和首位元素互换,并更新数组长度减一(heap[1] = heap[sz--]),随后从头部开始重整堆(down(1))
Java 完整模板:
int[] heap = new int[10010];
int sz = 0;
void swap(int a, int b) {
int c = heap[a];
heap[a] = heap[b];
heap[b] = c;
}
void up(int u) {
// 将「当前节点 i」与「父节点 i / 2」进行比较, 若父节点值更大, 则进行交换
int fa = u / 2;
if (fa != 0 && heap[fa] > heap[u]) {
swap(fa, u);
up(fa);
}
}
void down(int u) {
// 将当「前节点 cur」与「左节点 l」及「右节点 r」进行比较, 找出最小值, 若当前节点不是最小值, 则进行交换
int cur = u;
int l = u * 2, r = u * 2 + 1;
if (l <= sz && heap[l] < heap[cur]) cur = l;
if (r <= sz && heap[r] < heap[cur]) cur = r;
if (cur != u) {
swap(cur, u);
down(cur);
}
}
void add(int x) {
heap[++sz] = x;
up(sz);
}
int peek() {
return heap[1];
}
int pop() {
int ans = peek();
heap[1] = heap[sz--];
down(1);
return ans;
}
C++ 完整模板:
int heap[1010];
int sz = 0;
void up(int u) {
int fa = u / 2;
if (fa && heap[fa] >= heap[u]) {
swap(heap[fa], heap[u]);
up(fa);
}
}
void down(int u) {
int cur = u;
int l = cur * 2, r = cur * 2 + 1;
if (l <= sz && heap[l] < heap[cur]) cur = l;
if (r <= sz && heap[r] < heap[cur]) cur = r;
if (cur != u) {
swap(heap[cur], heap[u]);
down(cur);
}
}
void add(int x) {
heap[++sz] = x;
up(sz);
}
int peek() {
return heap[1];
}
int poll() {
int ans = peek();
heap[1] = heap[sz--];
down(1);
return ans;
}
模板运用
利用「上述模板」以及「小根堆如何当大根堆」使用,我们可以轻松解决本题。
-
起始先将逐元素进行符号翻转并入堆 -
执行 k次取出并重放操作(注意符号转换) -
统计所有元素之和,由于此时不再需要查询最值,可通过直接扫描数组的方式(注意符号转换)
Java 代码:
class Solution {
int[] heap = new int[10010];
int sz = 0;
public long pickGifts(int[] gs, int k) {
for (int x : gs) add(-x);
while (k-- > 0) add(-(int)Math.sqrt(-pop()));
long ans = 0;
while (sz != 0) ans += -heap[sz--]; // 没必要再维持堆的有序, 直接读取累加
return ans;
}
void swap(int a, int b) {
int c = heap[a];
heap[a] = heap[b];
heap[b] = c;
}
void up(int u) {
// 将「当前节点 i」与「父节点 i / 2」进行比较, 若父节点值更大, 则进行交换
int fa = u / 2;
if (fa != 0 && heap[fa] > heap[u]) {
swap(fa, u);
up(fa);
}
}
void down(int u) {
// 将当「前节点 cur」与「左节点 l」及「右节点 r」进行比较, 找出最小值, 若当前节点不是最小值, 则进行交换
int cur = u;
int l = u * 2, r = u * 2 + 1;
if (l <= sz && heap[l] < heap[cur]) cur = l;
if (r <= sz && heap[r] < heap[cur]) cur = r;
if (cur != u) {
swap(cur, u);
down(cur);
}
}
void add(int x) {
heap[++sz] = x;
up(sz);
}
int peek() {
return heap[1];
}
int pop() {
int ans = peek();
heap[1] = heap[sz--];
down(1);
return ans;
}
}
C++ 代码:
class Solution {
public:
int heap[1010];
int sz = 0;
long long pickGifts(vector<int>& gs, int k) {
for (int x : gs) add(-x);
while (k--) add(-sqrt(-poll()));
long ans = 0;
while (sz != 0) ans += -heap[sz--];
return ans;
}
void up(int u) {
int fa = u / 2;
if (fa && heap[fa] >= heap[u]) {
swap(heap[fa], heap[u]);
up(fa);
}
}
void down(int u) {
int cur = u;
int l = cur * 2, r = cur * 2 + 1;
if (l <= sz && heap[l] < heap[cur]) cur = l;
if (r <= sz && heap[r] < heap[cur]) cur = r;
if (cur != u) {
swap(heap[cur], heap[u]);
down(cur);
}
}
void add(int x) {
heap[++sz] = x;
up(sz);
}
int peek() {
return heap[1];
}
int poll() {
int ans = peek();
heap[1] = heap[sz--];
down(1);
return ans;
}
};
-
时间复杂度:建堆复杂度为 ;执行 k次操作复杂度为 ;构建答案复杂度为 。整体复杂度为 -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








