小米
前天写了武汉小米的「软件开发」岗位的 开奖情况, 。
15 薪是正常水平就不多说了,关键是 18k 这个数字,让不少拿到武汉小米 Offer 的同学感到不爽,觉得今年小米开的白菜价太低,多少带点侮辱性质。
但实际的情况,在那天的推文我就说了,在武汉,18k 这个数字是真不低了,我甚至还横向对比了其他武汉企业的软开薪资水平,武汉小米的 18k 确实属于中上水平。
这两天,上海小米的「soc 软开」岗位的开奖情况也出来了:
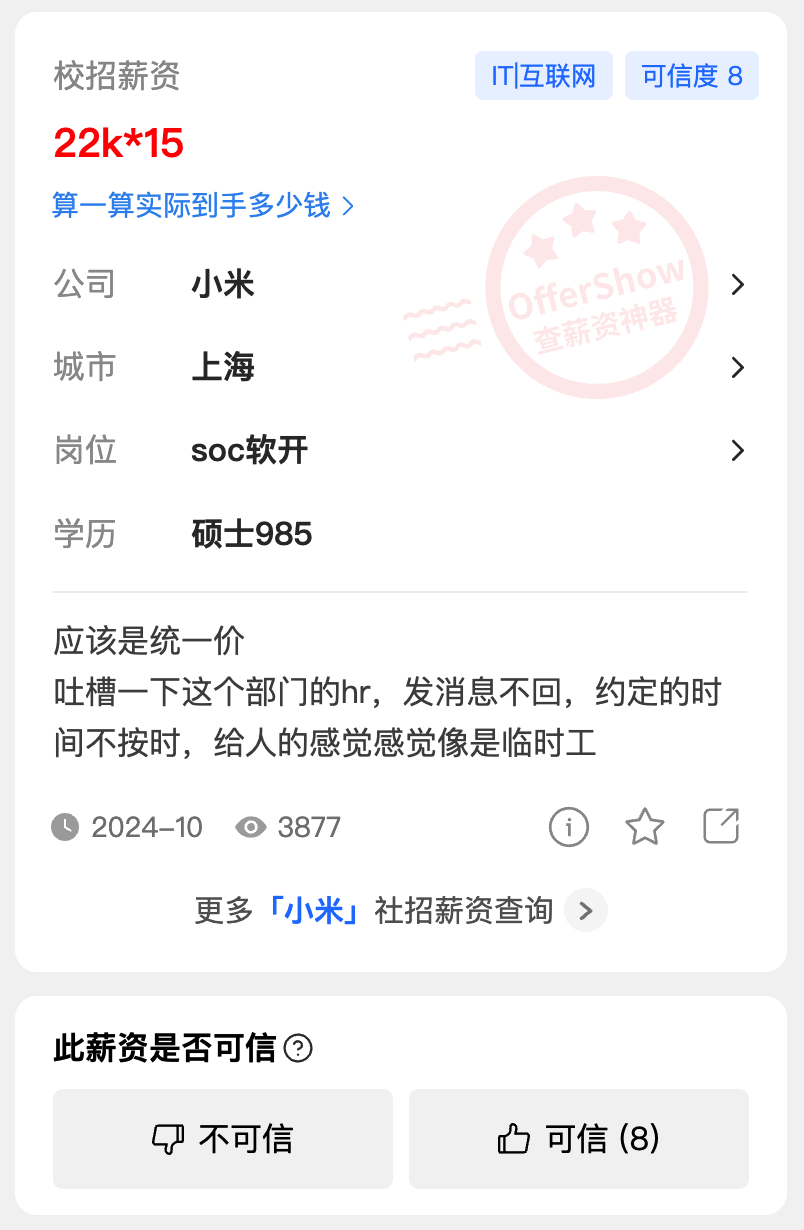
相比于之前的 武汉小米,同样是 985 硕士,同样是软开(只不过岗位性质定位在了芯片 SOC 方向上,历年小米在通用软开和 SOC 软开上的薪资待遇接近),开奖情况是 。
武汉是 18k,上海是 22k,两者薪资相差 4k(约 22%),但两个城市的生活成本,差的可不只是这点量级。
就拿消费大头,租房来说,武汉小米所在区域是东湖新技术开放区,附近的一居室公寓的租金基本在 1400 以内,而且这都是配套很好的公寓水平:
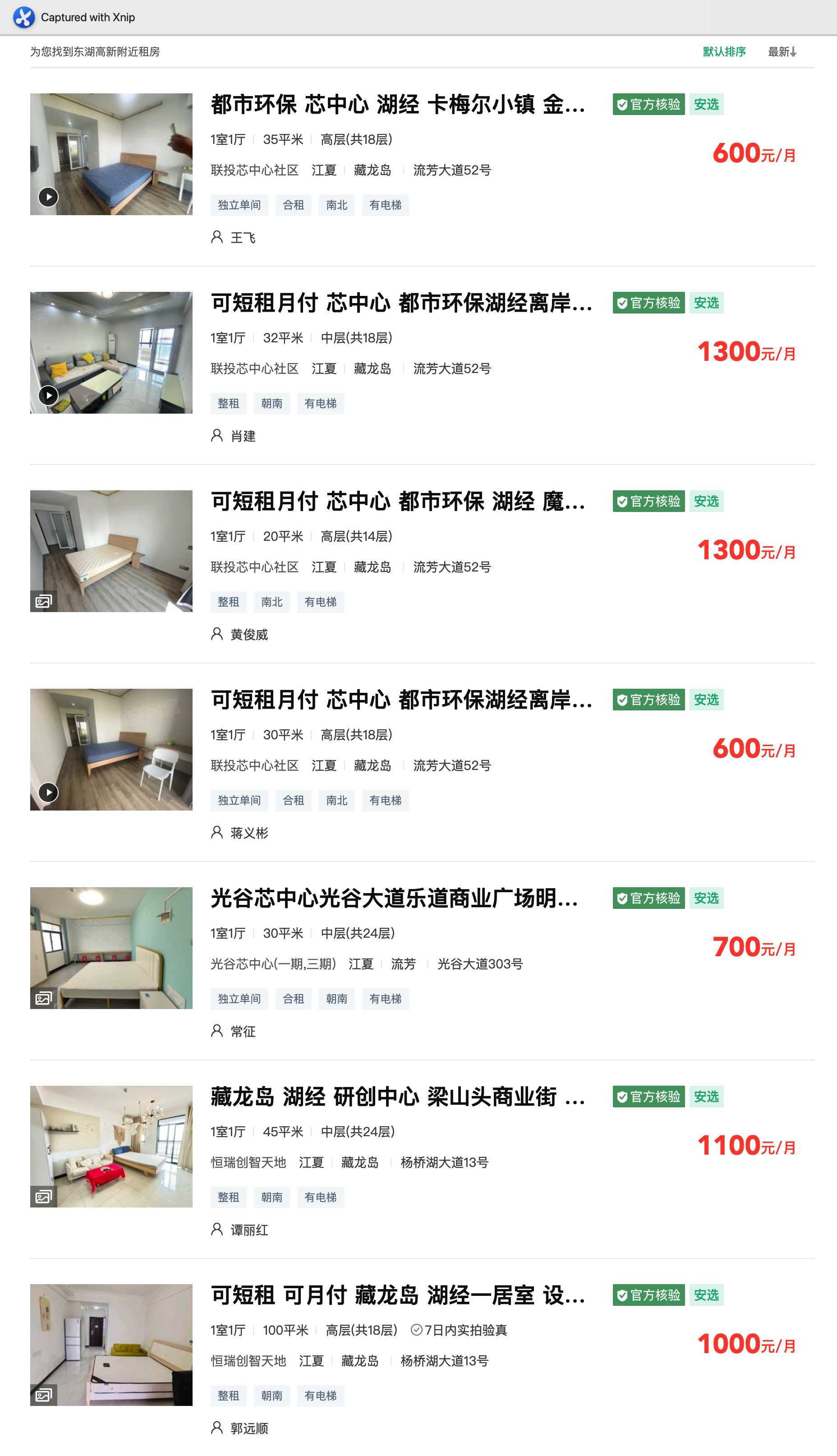
上海小米在沪闵路附近,想要住环境差不多的公寓,至少要多花 2k(薪资差一半没了):
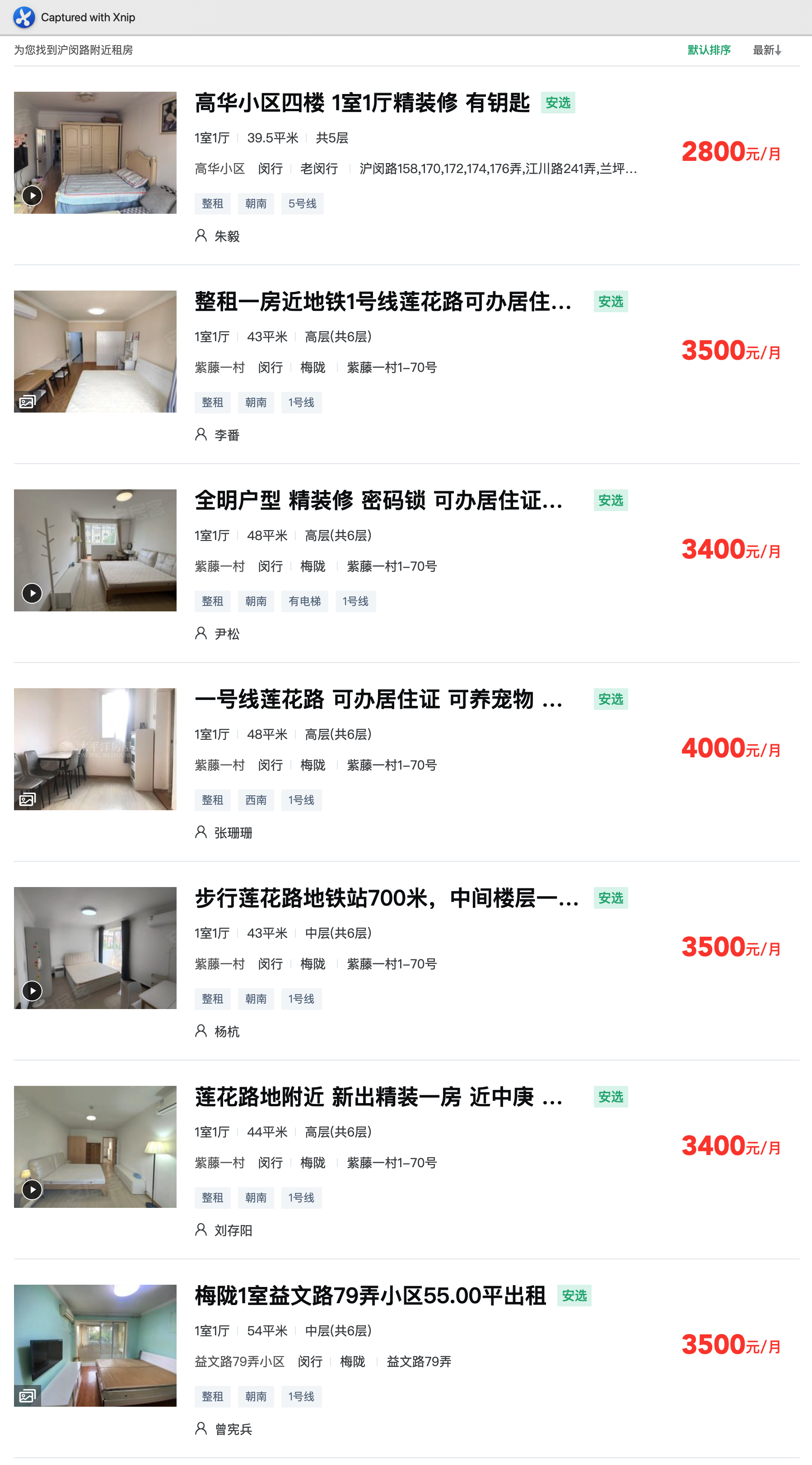
除去租房支出之后,剩下 2k 不到的薪资差,摊在一个月的伙食上面,也基本没剩啥的,如果在上海还想整点别的活动,那更是上不封顶。
经过这两个地区的白菜价对比,我估计当时嘲笑武汉小米 18k 的那个网友也不好意思笑了。毕竟上海小米白菜才 22k,武汉小米就给到 18k,这性价比不就挠一下就上来了吗?
对此,你怎么看,觉得两个白菜价哪个更有性价比?
...
回归主题。
来一道和「小米-校招-软开」相关的算法原题。
题目描述
平台:LeetCode
题号:87
使用下面描述的算法可以扰乱字符串 s 得到字符串 t :
-
如果字符串的长度为 1 ,算法停止 -
如果字符串的长度 > 1 ,执行下述步骤: -
在一个随机下标处将字符串分割成两个非空的子字符串。即,如果已知字符串 s,则可以将其分成两个子字符串x和y,且满足s = x + y。 -
随机 决定是要「交换两个子字符串」还是要「保持这两个子字符串的顺序不变」。即,在执行这一步骤之后, s可能是s = x + y或者s = y + x。 -
在 x和y这两个子字符串上继续从步骤 1 开始递归执行此算法。 给你两个 长度相等 的字符串s1和s2,判断s2是否是s1的扰乱字符串。如果是,返回true;否则,返回false。
-
示例 1:
输入:s1 = "great", s2 = "rgeat"
输出:true
解释:s1 上可能发生的一种情形是:
"great" --> "gr/eat" // 在一个随机下标处分割得到两个子字符串
"gr/eat" --> "gr/eat" // 随机决定:「保持这两个子字符串的顺序不变」
"gr/eat" --> "g/r / e/at" // 在子字符串上递归执行此算法。两个子字符串分别在随机下标处进行一轮分割
"g/r / e/at" --> "r/g / e/at" // 随机决定:第一组「交换两个子字符串」,第二组「保持这两个子字符串的顺序不变」
"r/g / e/at" --> "r/g / e/ a/t" // 继续递归执行此算法,将 "at" 分割得到 "a/t"
"r/g / e/ a/t" --> "r/g / e/ a/t" // 随机决定:「保持这两个子字符串的顺序不变」
算法终止,结果字符串和 s2 相同,都是 "rgeat"
这是一种能够扰乱 s1 得到 s2 的情形,可以认为 s2 是 s1 的扰乱字符串,返回 true
示例 2:
输入:s1 = "abcde", s2 = "caebd"
输出:false
示例 3:
输入:s1 = "a", s2 = "a"
输出:true
提示:
-
-
-
s1和s2由小写英文字母组成
朴素解法(TLE)
一个朴素的做法根据「扰乱字符串」的生成规则进行判断。
由于题目说了整个生成「扰乱字符串」的过程是通过「递归」来进行。
我们要实现 函数的作用是判断 是否可以生成出 。
这样判断的过程,同样我们可以使用「递归」来做:
假设 的长度为 , 的第一次分割的分割点为 ,那么 会被分成 和 两部分。
同时由于生成「扰乱字符串」时,可以选交换也可以选不交换。因此我们的 会有两种可能性:
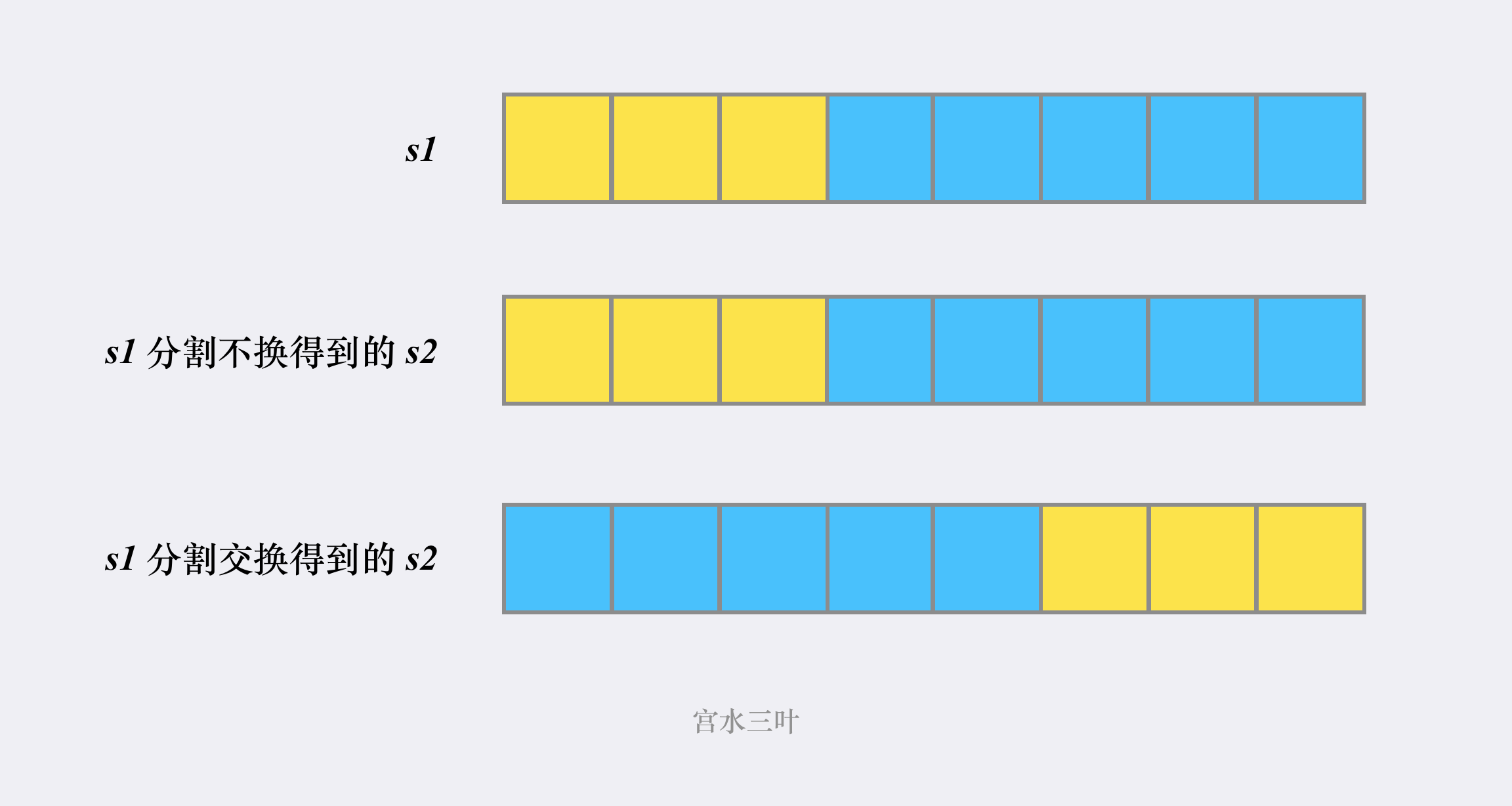
因为对于某个确定的分割点, 固定分为两部分,分别为 & 。
而 可能会有两种分割方式,分别 & 和 & 。
我们只需要递归调用 检查 的 & 部分能否与 「 的 & 」 或者 「 的 & 」 匹配即可。
同时,我们将「 和 相等」和「 和 词频不同」作为「递归」出口。
理解这套做法十分重要,后续的解法都是基于此解法演变过来。
Java 代码:
class Solution {
public boolean isScramble(String s1, String s2) {
if (s1.equals(s2)) return true;
if (!check(s1, s2)) return false;
int n = s1.length();
for (int i = 1; i < n; i++) {
// s1 的 [0,i) 和 [i,n)
String a = s1.substring(0, i), b = s1.substring(i);
// s2 的 [0,i) 和 [i,n)
String c = s2.substring(0, i), d = s2.substring(i);
if (isScramble(a, c) && isScramble(b, d)) return true;
// s2 的 [0,n-i) 和 [n-i,n)
String e = s2.substring(0, n - i), f = s2.substring(n - i);
if (isScramble(a, f) && isScramble(b, e)) return true;
}
return false;
}
// 检查 s1 和 s2 词频是否相同
boolean check(String s1, String s2) {
if (s1.length() != s2.length()) return false;
int n = s1.length();
int[] cnt1 = new int[26], cnt2 = new int[26];
char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
for (int i = 0; i < n; i++) {
cnt1[cs1[i] - 'a']++;
cnt2[cs2[i] - 'a']++;
}
for (int i = 0; i < 26; i++) {
if (cnt1[i] != cnt2[i]) return false;
}
return true;
}
}
-
时间复杂度: -
空间复杂度:忽略递归与生成子串带来的空间开销,复杂度为
记忆化搜索
朴素解法卡在了 个样例。
我们考虑在朴素解法的基础上,增加「记忆化搜索」功能。
我们可以重新设计我们的「爆搜」逻辑:假设 从 位置开始, 从 位置开始,后面的长度为 的字符串是否能形成「扰乱字符串」(互为翻转)。
那么在单次处理中,我们可分割的点的范围为 ,然后和「递归」一下,将 分割出来的部分尝试去和 的对应位置匹配。
同样的,我们将「入参对应的子串相等」和「入参对应的子串词频不同」作为「递归」出口。
Java 代码:
class Solution {
String s1; String s2;
int n;
int[][][] cache;
int N = -1, Y = 1, EMPTY = 0;
public boolean isScramble(String _s1, String _s2) {
s1 = _s1; s2 = _s2;
if (s1.equals(s2)) return true;
if (s1.length() != s2.length()) return false;
n = s1.length();
// cache 的默认值是 EMPTY
cache = new int[n][n][n + 1];
return dfs(0, 0, n);
}
boolean dfs(int i, int j, int len) {
if (cache[i][j][len] != EMPTY) return cache[i][j][len] == Y;
String a = s1.substring(i, i + len), b = s2.substring(j, j + len);
if (a.equals(b)) {
cache[i][j][len] = Y;
return true;
}
if (!check(a, b)) {
cache[i][j][len] = N;
return false;
}
for (int k = 1; k < len; k++) {
// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [0,i) & [i,n)」
if (dfs(i, j, k) && dfs(i + k, j + k, len - k)) {
cache[i][j][len] = Y;
return true;
}
// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [n-i,n) & [0,n-i)」
if (dfs(i, j + len - k, k) && dfs(i + k, j, len - k)) {
cache[i][j][len] = Y;
return true;
}
}
cache[i][j][len] = N;
return false;
}
// 检查 s1 和 s2 词频是否相同
boolean check(String s1, String s2) {
if (s1.length() != s2.length()) return false;
int n = s1.length();
int[] cnt1 = new int[26], cnt2 = new int[26];
char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
for (int i = 0; i < n; i++) {
cnt1[cs1[i] - 'a']++;
cnt2[cs2[i] - 'a']++;
}
for (int i = 0; i < 26; i++) {
if (cnt1[i] != cnt2[i]) return false;
}
return true;
}
}
-
时间复杂度: -
空间复杂度:
动态规划(区间 DP)
其实有了上述「记忆化搜索」方案之后,我们就已经可以直接忽略原问题,将其改成「动态规划」了。
「根据「dfs 方法的几个可变入参」作为「状态定义的几个维度」,根据「dfs 方法的返回值」作为「具体的状态值」。」
我们可以得到状态定义 :
「 代表 从 开始, 从 开始,后面长度为 的字符是否能形成「扰乱字符串」(互为翻转)。」
状态转移方程其实就是翻译我们「记忆化搜索」中的 dfs 主要逻辑部分:
// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [0,i) & [i,n)」
if (dfs(i, j, k) && dfs(i + k, j + k, len - k)) {
cache[i][j][len] = Y;
return true;
}
// 对应了「s1 的 [0,i) & [i,n)」匹配「s2 的 [n-i,n) & [0,n-i)」
if (dfs(i, j + len - k, k) && dfs(i + k, j, len - k)) {
cache[i][j][len] = Y;
return true;
}
从状态定义上,我们就不难发现这是一个「区间 DP」问题,区间长度大的状态值可以由区间长度小的状态值递推而来。
而且由于本身我们在「记忆化搜索」里面就是从小到大枚举 ,因此这里也需要先将 这层循环提前,确保我们转移 时所需要的状态都已经被计算好。
Java 代码:
class Solution {
public boolean isScramble(String s1, String s2) {
if (s1.equals(s2)) return true;
if (s1.length() != s2.length()) return false;
int n = s1.length();
char[] cs1 = s1.toCharArray(), cs2 = s2.toCharArray();
boolean[][][] f = new boolean[n][n][n + 1];
// 先处理长度为 1 的情况
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
f[i][j][1] = cs1[i] == cs2[j];
}
}
// 再处理其余长度情况
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
for (int j = 0; j <= n - len; j++) {
for (int k = 1; k < len; k++) {
boolean a = f[i][j][k] && f[i + k][j + k][len - k];
boolean b = f[i][j + len - k][k] && f[i + k][j][len - k];
if (a || b) f[i][j][len] = true;
}
}
}
}
return f[0][0][n];
}
}
C++ 代码:
class Solution {
public:
bool isScramble(string s1, string s2) {
if (s1 == s2) return true;
if (s1.length() != s2.length()) return false;
int n = s1.length();
vector<vector<vector<bool>>> f = vector<vector<vector<bool>>>(n, vector<vector<bool>>(n, vector<bool>(n + 1, false)));
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
f[i][j][1] = s1[i] == s2[j];
}
}
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
for (int j = 0; j <= n - len; j++) {
for (int k = 1; k < len; k++) {
bool a = f[i][j][k] && f[i + k][j + k][len - k];
bool b = f[i][j + len - k][k] && f[i + k][j][len - k];
if (a || b) f[i][j][len] = true;
}
}
}
}
return f[0][0][n];
}
};
Python 代码:
class Solution:
def isScramble(self, s1: str, s2: str) -> bool:
if s1 == s2:
return True
if len(s1) != len(s2):
return False
n = len(s1)
f = [[[False] * (n + 1) for _ in range(n)] for _ in range(n)]
for i in range(n):
for j in range(n):
f[i][j][1] = s1[i] == s2[j]
for lenv in range(2, n + 1):
for i in range(n - lenv + 1):
for j in range(n - lenv + 1):
for k in range(1, lenv):
a = f[i][j][k] and f[i + k][j + k][lenv - k]
b = f[i][j + lenv - k][k] and f[i + k][j][lenv - k]
if a or b:
f[i][j][lenv] = True
return f[0][0][n]
TypeScript 代码:
function isScramble(s1: string, s2: string): boolean {
if (s1 === s2) return true;
if (s1.length !== s2.length) return false;
const n = s1.length;
const f = new Array(n).fill(false).map(() => new Array(n).fill(false).map(() => new Array(n + 1).fill(false)));
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
f[i][j][1] = s1[i] === s2[j];
}
}
for (let len = 2; len <= n; len++) {
for (let i = 0; i <= n - len; i++) {
for (let j = 0; j <= n - len; j++) {
for (let k = 1; k < len; k++) {
const a = f[i][j][k] && f[i + k][j + k][len - k];
const b = f[i][j + len - k][k] && f[i + k][j][len - k];
if (a || b) f[i][j][len] = true;
}
}
}
}
return f[0][0][n];
};
-
时间复杂度: -
空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier,年度会员 有效期额外增加两个月,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








