C++五子棋人机对战源码分析与实战

本文还有配套的精品资源，点击获取

简介：五子棋是一种策略丰富的传统游戏，其AI算法的实现是计算机编程领域中的研究热点。本文将深入分析一个用C++编写的五子棋人机对战程序源码，包括AI算法的核心原理、数据结构设计、接口设计，以及优化算法的思路。源码中应用了Minimax和Alpha-Beta剪枝等搜索算法，并介绍了如何通过位操作优化棋盘状态的存储。此外，还讨论了高级搜索策略和深度学习技术在五子棋程序中的应用。本文通过分析"renju"文件中的源代码，帮助开发者掌握五子棋AI的实现，并提升在游戏开发或人工智能领域的技术能力。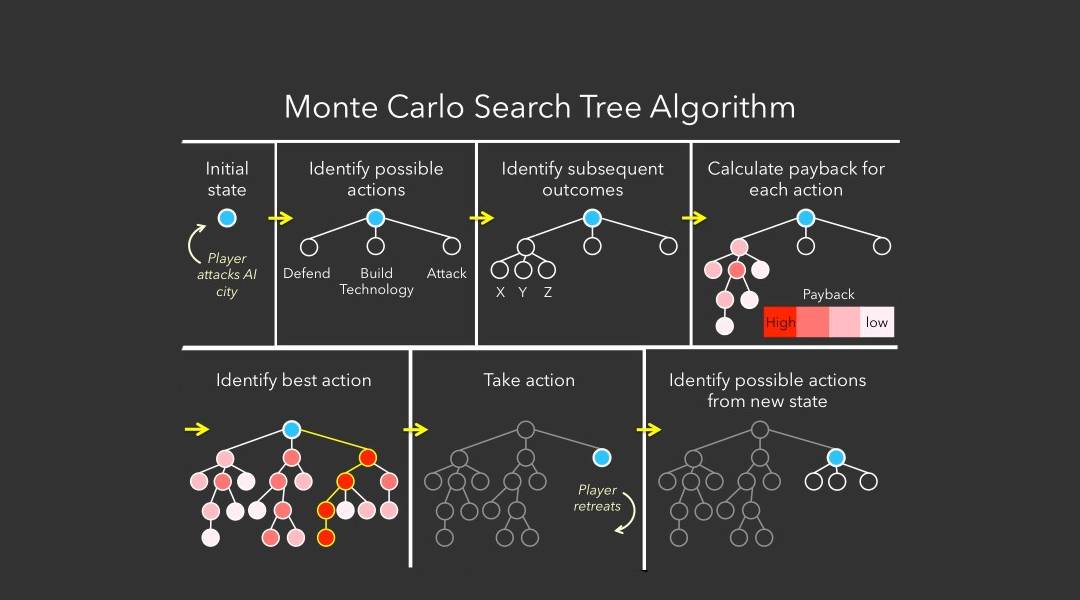

1. 五子棋游戏介绍

五子棋，一种两人对弈的纯策略型棋类游戏，由两人轮流在围棋棋盘上放置黑子与白子，任何一方先在横线、竖线或斜线上连成五子即为胜利。简单规则背后蕴藏着丰富的战术与战略，游戏的公平性、竞技性和娱乐性吸引了全世界范围内无数的爱好者。

作为一款经典的策略游戏，五子棋不仅仅是娱乐，它还是人工智能（AI）领域的研究热点之一。AI技术在五子棋上的应用展示了其对复杂决策问题的处理能力，如策略计算、模式识别和未来状态预测等。AI算法与五子棋的结合，不仅提升了游戏体验，还推动了相关技术的发展。

在本章中，我们将探讨五子棋的基本规则，分析游戏的策略和战术，并从技术角度简要介绍五子棋游戏的构成，为后续章节中关于AI算法和游戏开发技术的深入讨论打下基础。

2. AI算法核心原理

2.1 五子棋AI算法概述

2.1.1 算法的基本目标和评价标准

五子棋AI算法的目标是在给定的棋局状态下，自动寻找最佳的落子位置，以最大化胜率或特定的评分标准。算法的评价标准通常包括胜率、评分和计算速度等因素。在对弈过程中，AI需要评估当前棋局的优劣，并预测未来可能的棋局走向，以此选择最佳的落子策略。

AI的决策过程可以分解为搜索和评估两个主要步骤。搜索关注于遍历可能的落子序列，并生成游戏树；评估则关注于给定棋局状态一个数值评分，以反映其优劣。常见的评估函数基于棋型、棋子位置、势力分布等因素。此外，为了更好地预测对手的策略，可以引入如极大极小值（Minimax）算法这样的策略。

2.1.2 搜索与评估函数的作用

在五子棋AI中，搜索算法负责递归地探索棋局树，模拟不同落子方案的结果。该过程通常从当前棋局出发，向下遍历多层可能的落子序列，直至达到预定的搜索深度或遇到游戏结束状态。

评估函数的作用是为搜索算法提供评分依据。在五子棋AI中，评估函数通过分析棋盘上的棋型、棋子的位置、周围威胁等信息，对当前棋局状态进行打分。打分的结果将直接影响AI的搜索决策，引导AI选择潜在胜算更高的落子位置。

2.2 棋局评估基础

2.2.1 评估函数的构建原理

评估函数的构建原理是根据棋盘上的棋型和棋子分布来决定评分。常见的评估指标包括：

• 连续棋子的数量：计算当前玩家在横、竖、斜方向上连续棋子的数量。
• 活四、眠四、活三等棋型的威胁：分析对手是否拥有威胁较大的棋型。
• 控制力：评估玩家在棋盘中心和边缘的控制情况。
• 空间优势：衡量玩家控制的区域大小和未来可能发展的空间。

评估函数一般是一个加权和公式，将上述指标乘以相应的权重，再加总得到最终评分。

2.2.2 势力图与权重分析

势力图是一种形象化地表达棋盘上不同位置优劣的方法。在五子棋AI中，可以通过遍历棋盘，将每个位置按照当前局势赋予一定的分值，形成一张势力分布图。这样，AI在选择落子时，可以根据势力图提供的信息，优先选择分值高的区域进行落子。

权重分析指的是对评估函数中的各项指标分配权重的过程。权重的选择直接影响评估函数的性能和AI的下棋风格。例如，如果赋予“连续棋子数量”较高的权重，AI将更倾向于寻找连子机会；如果赋予“控制力”较高的权重，则AI可能会优先考虑对棋盘中心的控制。

为了科学地确定权重，常用的方法包括线性回归、遗传算法等，这些方法能够基于大量棋局数据和结果，学习出最佳的权重配置。

graph TD
A[开始] --> B[棋局评估]
B --> C[计算棋型评分]
C --> D[计算控制力]
D --> E[计算威胁度]
E --> F[生成势力图]
F --> G[应用权重计算最终评分]
G --> H[结束]

在五子棋AI开发中，棋局评估的基础是实现一个既能够准确反映棋局状态，又能够适应不同玩家风格的评估函数。准确的评估可以帮助AI在实际对弈中做出更合理的决策，提高胜率。因此，棋局评估基础是五子棋AI核心算法的重要组成部分。

请注意，以上内容仅为章节的简要概览，实际的文章需要在每个段落中进一步扩展和深入分析，以确保每个部分都能达到要求的字数。

3. 数据结构设计

3.1 棋盘数据结构

3.1.1 二维数组与位操作表示

在五子棋的程序设计中，棋盘数据结构的选择是至关重要的。它直接影响到游戏的执行效率和编码的复杂度。二维数组是实现棋盘最直观的方式，它简单且易于理解。

#define BOARD_SIZE 15 // 定义棋盘大小为15*15
int board[BOARD_SIZE][BOARD_SIZE] = {0}; // 初始化一个15*15的棋盘

然而，为了提高效率和空间利用率，位操作提供了更为高效的数据结构选择。通过对棋盘上的每一行、每一列、每一个对角线进行位编码，可以将原本需要存储15*15个元素的二维数组，简化为只需存储几个整型变量的位棋盘。这种方式不仅减少了内存的使用，还可以通过位运算快速判断棋型。

unsigned short board = 0; // 初始化一个位棋盘，使用16位整型变量

3.1.2 动态数组的内存管理

在实现棋盘动态扩展的过程中，动态数组的使用是必不可少的。为了实现高效的内存管理，应该选择合适的数据结构来存储历史棋盘状态、AI的决策过程等。

struct DynamicArray {
    void *array;    // 指向数组的指针
    size_t capacity; // 数组的容量
    size_t length;  // 当前存储的元素个数
    size_t element_size; // 每个元素的大小
};

void* reallocate(void *old, size_t new_size) {
    // 重新分配内存空间的函数
    // 返回指向新分配内存的指针
}

在代码中， DynamicArray 结构体用于定义动态数组。通过 reallocate 函数，动态数组可以根据需求在运行时进行扩展或收缩，使得内存资源得到更合理的利用。

3.2 搜索树的设计

3.2.1 棋局状态的存储方式

为了进行有效的搜索，每个棋局状态都需要被存储和管理。在五子棋中，我们可以定义一个棋局节点来保存游戏的当前状态。

typedef struct GameState {
    int board[BOARD_SIZE][BOARD_SIZE]; // 当前棋盘状态
    int turn; // 当前轮到的玩家
    struct GameState *parent; // 指向父节点的指针
    int move; // 从父节点到当前节点的移动
} GameState;

GameState 结构体中， board 保存棋盘状态， turn 保存当前轮到的玩家， parent 和 move 用于构建搜索树，它们分别表示指向父节点的指针和当前节点是从哪个父节点移动过来的。

3.2.2 节点的生成与遍历

棋局状态的搜索依赖于对节点的生成与遍历。在五子棋中，每当一方落子，就会生成一个新的节点。我们通常使用递归回溯的方式生成所有可能的节点，并对这些节点进行搜索。

void generateMoves(GameState *state, GameState **moves, int *moveCount) {
    // 根据当前状态生成所有可能的移动
    // 并计算可能的移动数量
}

generateMoves 函数用于生成所有可能的移动，更新 moveCount 和 moves 参数。这样的设计使得我们可以通过递归搜索树的每个分支，以实现深度优先搜索（DFS）。

3.3 数据结构的实现逻辑分析

五子棋的数据结构设计需要考虑存储效率、访问速度和逻辑清晰度。二维数组和位操作结合使用提供了多种可能性。动态数组的设计保证了节点的灵活扩展和高效的内存利用。棋局状态的节点设计为搜索树提供了基础框架，而节点的生成和遍历是实现搜索算法的核心。在实现这些数据结构时，我们应当遵循代码复用、清晰逻辑和高效执行的原则。

接下来，我们将深入探讨搜索算法的实现，特别是Minimax算法和Alpha-Beta剪枝技术，这些算法是实现五子棋AI的关键部分。通过这些算法，我们可以在复杂的棋局中找到最优或近似最优的决策路径。

4. 搜索算法实现

4.1 Minimax算法详解

4.1.1 Minimax原理及伪代码实现

Minimax算法是五子棋AI设计中用于决定最优走棋的关键算法。其基本原理是假设双方都尽可能地使自己的利益最大化，一方试图达到最大利益时，另一方则会相应地作出最小化该方利益的决策，反之亦然。简而言之，这是一种递归算法，用于最小化对手可能的最大收益。

以下是一个基本的Minimax算法的伪代码实现：

def minimax(position, depth, alpha, beta, maximizing_player):
    if depth == 0 or position.is_terminal():
        return position.evaluate()  # 评估函数计算当前棋局评分
    if maximizing_player:
        best_score = -∞
        for each child:
            v = minimax(child, depth - 1, alpha, beta, False)
            best_score = max(best_score, v)
            alpha = max(alpha, v)
            if beta <= alpha:
                break
        return best_score
    else:
        best_score = ∞
        for each child:
            v = minimax(child, depth - 1, alpha, beta, True)
            best_score = min(best_score, v)
            beta = min(beta, v)
            if beta <= alpha:
                break
        return best_score

在此伪代码中， position 表示当前棋局的状态， depth 是搜索深度， alpha 和 beta 是alpha-beta剪枝的参数，而 maximizing_player 是一个布尔值，表示是否为最大化玩家（AI）的回合。

逻辑分析： 1. 递归终止条件 ：如果当前深度为0或棋局已结束（ is_terminal() 返回真），直接返回当前棋局的评分。 2. 最大玩家（AI） ：如果是AI的回合，遍历所有可能的走法，对每一个子走法递归调用 minimax ，选择分数最高的一个。 3. 最小玩家 ：如果是对手的回合，遍历所有可能的走法，对每一个子走法递归调用 minimax ，选择分数最低的一个。 4. 剪枝优化 ：在递归过程中，利用 alpha 和 beta 进行剪枝。如果当前最佳分数已经小于等于beta，则不再继续搜索，这可以防止评估已经不可能被选择的走法，从而提升算法效率。

4.1.2 启发式评估的优化技巧

在实践中，为了提升Minimax算法的效率和准确度，会引入一些启发式方法来改进评估函数。评估函数是算法中决定棋局优劣的核心因素，它的设计直接影响到AI的下棋水平。

下面列举一些常见的优化技巧：

• 棋型计分 ：对于连成一线的棋子进行计分，例如：单活三、双活三、眠三、活四等。
• 棋型权重 ：根据棋型的重要程度给予不同的权重值。
• 子力平衡 ：鼓励AI在棋盘上均衡布局，防止出现明显的薄弱点。
• 连子长度 ：对于五子棋来说，连子越长越有价值，需要对长连子给予较高的评分。
• 边界效应 ：棋盘的四个角和边缘的棋子往往更难被攻击，可以为这些位置的棋子赋予更高的权重。

具体的评估函数改进伪代码如下：

def evaluate_position(position):
    score = 0
    # 分别计算各种棋型的得分
    score += count_threes(position) * weight_for_threes
    score += count_fours(position) * weight_for_fours
    # ... 其他棋型计分逻辑
    # 考虑棋子位置
    score += position_count_in_center(position) * center_weight
    score += position_count_at_edges(position) * edge_weight
    # ... 其他位置价值计分逻辑
    return score

在此伪代码中， count_threes 、 count_fours 等函数用于计算棋盘上特定棋型的数量， position_count_in_center 、 position_count_at_edges 函数用于计算棋子在棋盘中心和边缘的数量。 weight_for_threes 、 weight_for_fours 等变量代表了不同棋型的权重值， center_weight 、 edge_weight 等变量则代表了不同位置的权重值。

4.2 Alpha-Beta剪枝机制

4.2.1 Alpha-Beta剪枝原理

Alpha-Beta剪枝是一种提升Minimax算法效率的优化手段。它减少了不必要的节点评估，通过记录已搜索过的路径中发现的最优值，来减少搜索树的大小。

原理简述 ：

• Alpha（α）值 ：表示在当前路径下，最大化玩家（AI）所能得到的最佳分数。
• Beta（β）值 ：表示在当前路径下，最小化玩家（对手）所能得到的最佳分数。

在搜索过程中，当我们发现一个节点的值对于最大化玩家来说已经低于之前的最佳值（即小于alpha值），那么这个节点及所有子节点都不再需要评估。同样的，如果一个节点的值对于最小化玩家来说已经高于之前的最佳值（即大于beta值），那么这个节点及所有子节点也不再需要评估。

4.2.2 实际应用中的效率提升策略

Alpha-Beta剪枝能够在维持Minimax算法正确性的基础上大幅提升搜索效率。为了更好地利用这种剪枝机制，有一些策略可以帮助进一步提升性能：

• 启发式排序 ：按照启发式评分对可能的走法进行排序，使得更有可能被选中的走法先被评估。
• 迭代加深 ：首先进行深度较浅的搜索，然后再逐渐增加深度，这样可以帮助快速剪枝。
• 置换表 （Transposition Table）：存储之前已经评估过的节点的评估结果，对于重复的节点可以直接使用之前的结果。

以下是应用Alpha-Beta剪枝时的伪代码：

def alpha_beta(position, depth, alpha, beta, maximizing_player):
    if depth == 0 or position.is_terminal():
        return position.evaluate()
    if maximizing_player:
        for each child:
            alpha = max(alpha, alpha_beta(child, depth - 1, alpha, beta, False))
            if beta <= alpha:
                break  # 剪枝
        return alpha
    else:
        for each child:
            beta = min(beta, alpha_beta(child, depth - 1, alpha, beta, True))
            if beta <= alpha:
                break  # 剪枝
        return beta

在上面的伪代码中， alpha 和 beta 参数用于记录剪枝的阈值。通过这种方式，算法能够跳过大量的无效搜索分支，从而显著提升搜索效率，加快找到最佳走法的速度。

本章节的内容通过深入的理论解释和实际应用策略，展示了五子棋AI设计中Minimax算法和Alpha-Beta剪枝机制的核心原理与实现方法。通过这些优化技巧，五子棋AI的性能得到显著提升，使其能够更智能地进行决策。

5. 性能优化与实战应用

随着技术的不断发展，五子棋AI的性能优化和实战应用成为了提升算法效率和用户体验的关键。在本章中，我们将深入探讨如何通过位操作技术和高级搜索策略来优化五子棋AI的性能，并分析深度学习技术如何进一步推动AI的发展。

5.1 位操作与棋盘状态的优化

5.1.1 位操作的原理及优势

位操作是一种使用布尔运算符如AND(&)、OR(|)、NOT(~)、XOR(^)、左移(<<)和右移(>>)对二进制位进行直接操作的技术。在五子棋AI中，位操作能够有效地加快棋盘状态的处理速度，减少内存消耗，是优化棋盘状态存储与检索的重要手段。

例如，我们可以在一个整型变量中存储棋盘的一个状态，每个位代表一个棋盘格。对于一个15x15的棋盘，我们可以用一个32位整型数组（4个15x15棋盘）或者64位整型（8个15x15棋盘）来表示整个棋局状态，大大减少了内存占用。

5.1.2 状态压缩技术应用实例

状态压缩是指使用位操作将一个大状态压缩到更小的空间，同时还要保持快速访问状态的能力。下面的代码片段展示了如何使用位操作来设置和获取棋盘状态：

def set_bit(board, row, col, player):
    # 根据行列位置设置棋盘上某点的状态，player为1表示玩家一，0表示玩家二
    return board | (1 << (row * 15 + col))

def get_bit(board, row, col):
    # 获取棋盘上某点的状态
    return (board >> (row * 15 + col)) & 1

# 初始化棋盘状态
board = 0

# 玩家一在(7,7)位置落子
board = set_bit(board, 7, 7, 1)

# 查询(7,7)位置的状态
player = get_bit(board, 7, 7)  # 返回值为1，表示玩家一在此位置落子

通过状态压缩技术，AI算法可以更快地处理棋盘状态变化，提高搜索效率，从而在实战中表现得更加迅速和精确。

5.2 高级搜索策略与深度学习

5.2.1 蒙特卡洛树搜索与应用

蒙特卡洛树搜索（MCTS）是一种高效的搜索策略，特别适用于大规模或复杂的游戏如围棋和五子棋。MCTS通过构建一棵树，每层节点代表一个棋局状态，并在树中进行随机模拟来评估棋局的胜率。

五子棋AI中实现MCTS需要考虑以下几个步骤：

1. 选择：从根节点开始，选择最佳子节点。
2. 扩展：如果到达了非完全扩展的节点，则创建新的子节点。
3. 模拟：从新扩展的节点进行随机游戏直到结束，记录结果。
4. 反向传播：根据模拟结果更新节点的统计信息，即胜率。

MCTS的伪代码如下：

def MCTS(root):
    node = select(root)
    leaf = expand(node)
    result = rollout(leaf)
    backpropagate(leaf, result)

5.2.2 深度学习在五子棋AI中的融合

深度学习与五子棋AI的结合，特别是结合卷积神经网络（CNN）和强化学习，已经在AlphaGo的胜利中显现了巨大的潜力。深度学习模型可以用来评估棋局或直接生成下一步的最优动作。

五子棋AI可以采用以下策略融合深度学习：

• 评估网络 ：训练一个神经网络来评估棋盘状态的优劣，作为搜索树节点的评估函数。
• 策略网络 ：训练一个网络来直接预测下一步的最佳落子点。

例如，可以使用TensorFlow或PyTorch等深度学习框架来构建和训练以下结构的网络：

import tensorflow as tf
from tensorflow.keras.layers import Input, Conv2D, Dense

def create_model():
    inputs = Input(shape=(15, 15, 1))
    x = Conv2D(32, kernel_size=3, padding='same', activation='relu')(inputs)
    x = Conv2D(64, kernel_size=3, padding='same', activation='relu')(x)
    x = Conv2D(1, kernel_size=1, padding='valid', activation='sigmoid')(x)
    model = tf.keras.Model(inputs=inputs, outputs=x)
    ***pile(optimizer='adam', loss='binary_crossentropy')
    return model

model = create_model()

在这个模型中，卷积层用于捕获棋盘上复杂的空间模式，输出层则输出每个可能落子点的胜率评估值。通过与蒙特卡洛树搜索结合，这些评估值可以大大提升搜索效率和质量。

结合深度学习与高级搜索策略，五子棋AI可以实现对人类顶尖选手的超越，展现了人工智能在策略游戏领域内的巨大潜力和应用前景。

本文还有配套的精品资源，点击获取

简介：五子棋是一种策略丰富的传统游戏，其AI算法的实现是计算机编程领域中的研究热点。本文将深入分析一个用C++编写的五子棋人机对战程序源码，包括AI算法的核心原理、数据结构设计、接口设计，以及优化算法的思路。源码中应用了Minimax和Alpha-Beta剪枝等搜索算法，并介绍了如何通过位操作优化棋盘状态的存储。此外，还讨论了高级搜索策略和深度学习技术在五子棋程序中的应用。本文通过分析"renju"文件中的源代码，帮助开发者掌握五子棋AI的实现，并提升在游戏开发或人工智能领域的技术能力。

本文还有配套的精品资源，点击获取