坐标计算距离公式 火星坐标系_火星，我们来啦！

引言

7 月 23 日 2 时 41 分，我国首个独立火星探测器“天问一号”成功发射。中华民族对于外太空的探索从来没有停止自己的脚步，“天问一号”巧用屈原长诗《天问》表达了中华民族对真理追求的坚韧和执着！那么“天问一号”是怎样去火星的？和地球上两点之间往返不同，去火星要复杂得多。地球和火星都是环绕太阳旋转的行星，而由于椭圆形轨道的半径不同，两者公转周期也不同，导致地球和火星之间的直线距离呈周期性变化。最近时为 5460 万千米，最远时可达 4 亿千米。因此需要提前对探测器飞行路线进行规划。

图 1: 火星探测器“天问一号”发射升空

理论上探测器可以沿着任意路径到达火星，但是有一条称为“霍曼转移轨道”的飞行路径效率最高。该轨道是由德国物理学家霍曼在 1925 年首次提出的，途中只需两次引擎推进，相对节省燃料。

图 2: 编号 2 的半椭圆就是霍曼转移轨道

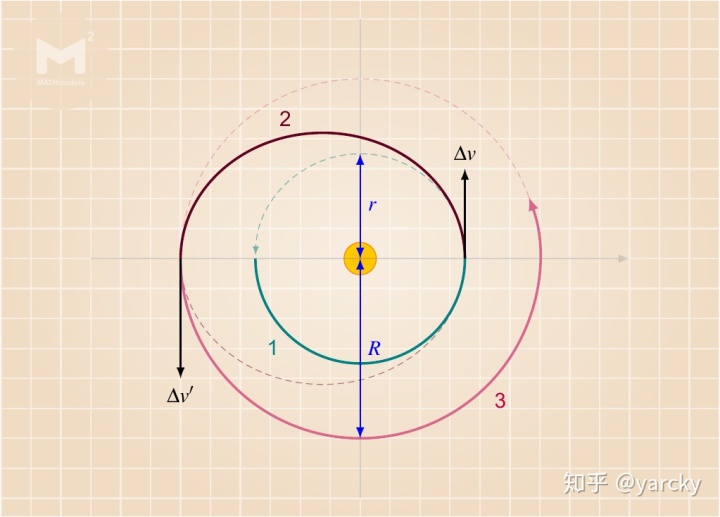
例如图 2 是将航天器从低轨道 1 送往较高轨道 3 的霍曼转移轨道。航天器在原先轨道 1 上瞬间加速后，进入一个椭圆轨道 2。航天器由此椭圆轨道的近拱点开始，抵达远拱点后再瞬间加速，进入另一个圆轨道 3，此即为目标轨道。要注意的是，三个轨道的半长轴是越来越大的，因此两次引擎推进皆是加速。

图 3: 成功到达火星

对于地球到火星的霍曼转移轨道，若取地球和火星的椭圆形轨道为近似圆形轨道，则霍曼转移轨道呈环绕太阳的椭圆形。近日点在地球轨道，远日点在火星轨道。从地球发射的飞船首先加速到霍曼转移轨道速度，到达火星轨道后再加速到火星环绕速度。若要降落火星地表，则可省去第二次加速直接坠入火星。为了探测器和火星同时到达同一个点，探测器必须在特定的时间范围内发射。这个特定的时间范围称为“发射窗口”。若错过“发射窗口”，则需要再等两年多的时间。

图 4: 错过发射窗口

本文使用简单的数理知识建立模型来确定“发射窗口”期间地球和火星的相对位置，并确定两次“发射窗口”之间的时间间隔。

模型

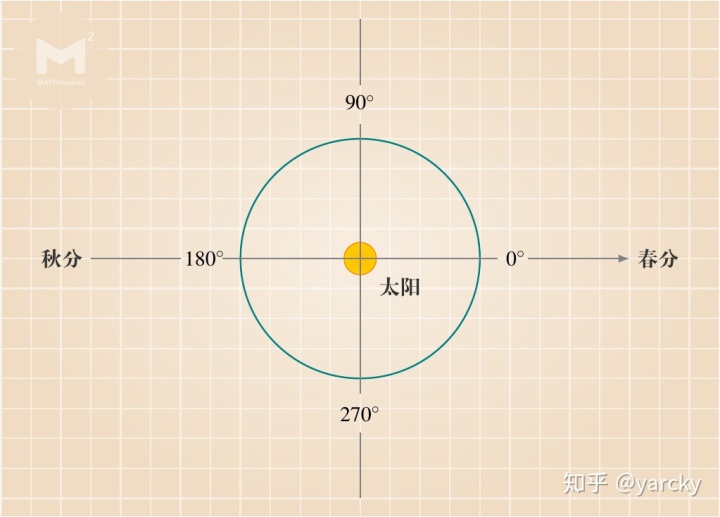
为了描述地球、火星和探测器的运动，我们需要一个以太阳为参照点的坐标系。如图 5 所示，我们以地球绕太阳公转的轨道平面（黄道）作为基准平面，用 0

到 360

来给出从太阳中心看时天体围绕黄道的位置。由于在黄道上没有明显可以作为黄道经度 0

的点，因此春分点常被指定为黄经 0

的位置。这种坐标系在天文学中被称为黄道坐标系，相应的坐标被称为日心经度（太阳经度）。

图 5: 黄道坐标系和日心经度

地球和火星，以及火星探测器的动力学是非常复杂的。为了简化问题，我们做出了一些假设：

• 地球和火星的轨道都是以太阳为中心的圆。实际上地球和火星的轨道并不是圆，而是略呈椭圆。相比之下，地球的轨道比火星更圆。
• 地球和火星都以恒定的速度绕太阳运动。由普勒第二定律可知，单位时间内行星与太阳的连线所扫过的面积相等。因此行星在近日点速度大，在远日点速度小。但由于地球和火星的轨道非常接近圆，因此公转过程中速度变化不太。
• 地球和火星的轨道在同一平面上。实际上地球和火星的公转轨道并不在同一平面内，但两平面非常接近，仅有微小的夹角。

注意，以上假设严格上来讲都不正确。但在这些假设下，问题将得到极大地简化，并且在此基础上对“发射窗口”计算的精度已经足够说明问题。

图 6: 地球和火星轨道以及太阳

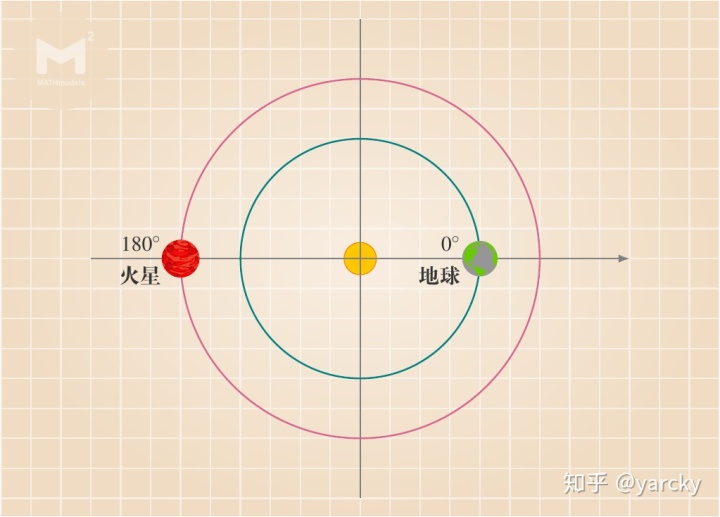
为了方便演示（图 6），我们将地球放置于日心经度为 0

位置（探测器在此位置发射），将火星放置于日心经度为 180

位置（探测器在此位置登入火星）。那么霍曼转移轨道就是连接处于 0

地球和处于 180

火星的椭圆（图 7）。

图 7: 地球和火星之间的霍曼转移轨道

图 8: 霍曼转移轨道半长轴的计算

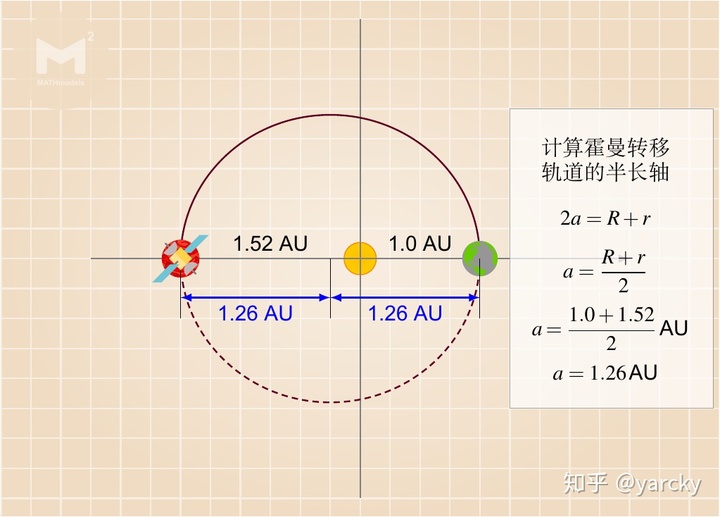
地球到太阳的平均距离为 1 个天文单位，即 1.0 AU。而火星到太阳的平均距离为 1.524 AU。因此很容易计算出霍曼转移轨道半长轴为

开普勒第三定律指出，绕以太阳为焦点的椭圆轨道运行的所有行星，其公转周期

的平方与其椭圆轨道半长轴

的立方成正比，即

其中

为常数。若以天文单位 AU 为长度单位，以年为时间单位。对于地球有

AU，

年，则可求出

。据此可以求出火星的公转周期为

同样，还可以求出探测器绕椭圆形霍曼转移轨道运动的周期为

从地球到达火星，只需要沿着霍曼转移轨道飞行半周，因此大约需要 259 天。

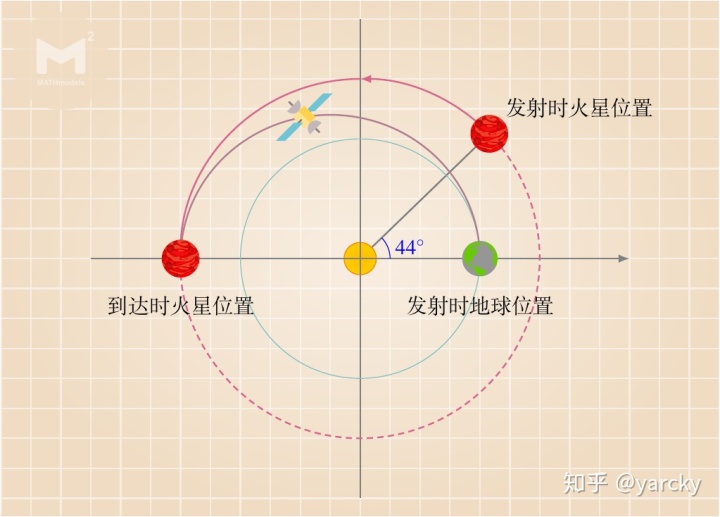
火星绕太阳公转一周（360

）需要 687 天，这意味着在探测器沿着霍曼转移轨道飞行半周的 259 天中，火星转过的角度为

要计算探测器发射时火星的位置，则从火星接受到探测器的位置（180

）上减去火星转过的角度 136

，即 180

- 136

= 44

。因此，如果想让探测器到达火星轨道时正好能够与火星相遇，则需要在火星日心经度刚好领先地球 44

时从地球上发射探测器（图 9）。

图 9: 发射探测器时火星相对地球位置

接下来我们考虑如果错过发射窗口，需要多长时间才能等到下一次发射窗口。由于地球公转的角速度大于火星，只要地球刚好比火星多绕太阳转一周时，就是下一次发射窗口（图 10）。

图 10: 相对于图 9 的下一次发射窗口

因此，两次发射窗口的时间间隔

可表示为

代入地球和火星的公转周期可得

从几何角度解释也容易理解：在 779 天内地球绕太阳运动了 2 周 48 度角，火星运动了 1 周 48 度角，火星和地球的相对位置又回到了 779 天前（相差 44

角）。

实践

在上文的模型中，我们介绍了霍曼转移轨道，并计算得到了“发射窗口”期间地球和火星的相对位置，以及两次“发射窗口”的时间间隔。我们还可以动手绘制霍曼转移轨道。首先准备一张方格纸，并约定 1 分米表示一个天文单位。然后把一颗图钉固定在方格纸的正中间，表示太阳的位置。将绳长分别调整到

分米（地球公转轨道半径的两倍）和

分米（火星公转轨道半径的两倍），就可以按照图 11 所示的方法绘出地球和火星的圆形轨道。

图 11: 用绳和一颗图钉绘制圆形轨道

接下来我们绘制表示霍曼转移轨道的椭圆。椭圆的焦距为 0.26 分米，表示太阳的图钉是椭圆的一个焦点。如果我们认为太阳的坐标为 (0,0)，则椭圆的另一个焦点为 (-0.52,0)，我们在该焦点处也固定一颗图钉。把绳长调整为椭圆半长轴与焦距之和两倍长度，即

分米，就可以按照图 12 所示的方法绘出椭圆霍曼转移轨道。

图 12: 用绳和两图钉绘制霍曼转移轨道

结论

本文通过建立数学型和实践绘图，介绍了“霍曼转移轨道”，并计算得到了“发射窗口”为火星的太阳经度领先地球 44

时，两次“发射窗口”的时间间隔为 779 天（约 26 个月）。在实际飞行时，火箭的发射条件会由于总装调试进程、火箭状态和天气等原因推迟，因而发射也并不需要严格遵循 26 个月的间隔，这仅是理论值。例如，2011 年 11 月 26 日好奇号火星车发射，它和 2013 年 11 月 18 日发射的大气专家轨道器仅相隔 24 个月。由于各探测窗口条件不同，各探测器使用的火箭性能和飞行方案不同，最终的探测器霍曼转移轨道飞行距离可以轻易长达 4-7 亿千米，耗时 6-11 个月不等。对于 2020 年从地球出发的几个火星探测器而言（包括我国的天问一号），大致都需要 7 个月左右时间，于 2021 年 2 月前后分别抵达火星。

参考资料

[1] Wikipedia contributors. Tianwen-1 — Wikipedia, the free encyclopedia, 2020: https://en.wikipedia.org/wiki/Tianwen-1

[2] California Institute of Technology. Jet propulsion laboratory, 2020: https://www.jpl.nasa.gov/edu/teach/activity/lets-go-to-mars-calculating-launch-windows/

[3] Ariel Zych. Scale solar system orbits—and satellites!, 2018: https://www.sciencefriday.com/educational-resources/scale-solar-system-orbits-and-satellites/