学生训练典型题目收集【1】

$\color{Blue}{学生训练典型题目收集【1】}$

在高三学生的课时作业中，每年都会出现一些让我们感觉典型的题目，现加以收集如下：

$\color{Red}{【001】}$

某个命题与自然数\(n\)有关，若\(n=k(k\in N^*)\)时命题成立，那么可以推得当\(n=k+1\)时命题也成立。现已知当\(n=5\)时，该命题不成立，那么可以推得（\(\;\;\;\;\;\;\;\)）

A.当\(n=6\)时，该命题不成立 \(\;\;\;\;\;\;\;\) B.当\(n=6\)时，该命题成立 \(\;\;\;\;\;\;\;\) C.当\(n=4\)时，该命题不成立 \(\;\;\;\;\;\;\;\) D.当\(n=4\)时，该命题成立

[答案]选C.解析：本题目考查数学归纳法和命题的等价。

原命题认定为真，则其逆否命题是：“若\(n=k+1(k\in N^*)\)时命题不成立，则\(\;\;n=k\;\;\)时命题也不成立。”也为真，这样由于题目已知当\(n=5\)时，该命题不成立，则可以推出当\(n=4\)时，该命题不成立，而且当\(n=3,2,1\)时，该命题也不成立。

$\color{Red}{【002】}$

已知\(x^2+y^2\leq 1\)，求\(|2x+y-2|+|x+3y-6|\)的最小值？

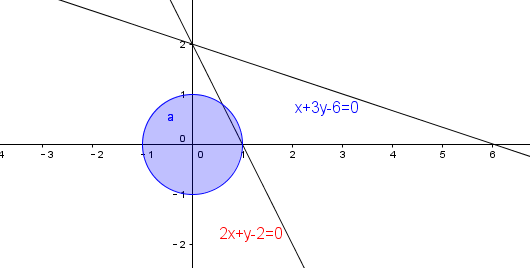
思路一：转化为点线距

为什么想到这个，我们发现\(|2x+y-2|+|x+3y-6|=\sqrt{5}\cfrac{|2x+y-2|}{\sqrt{5}}+\sqrt{10}\cfrac{|x+3y-6|}{\sqrt{10}}\)，

其中表达式\(\cfrac{|2x+y-2|}{\sqrt{5}}\)和\(\cfrac{|x+3y-6|}{\sqrt{10}}\)分别表示园内及圆上的动点到两条直线的距离，所以可以把“数”的问题转化为“形”的问题。

思路二：三角代换，令\(x=R\cos\theta，y=R\sin\theta，R\in[0，1]\)，则\(|2x+y-2|+|x+3y-6|\ge|3R\cos\theta+4R\sin\theta-8|=|5R\sin(\theta+\phi)-8|\)

思路三：

$\color{Red}{【003】}$

存在函数\(f(x)\)满足：对任意的\(x\in R\)都有（\(\;\;\; D\;\;\;\;\)）

A、\(f(sin2x)=sinx\) \(\;\;\; \;\;\;\;\) B、$f(sin2x)=x^2+x $ \(\;\;\; \;\;\;\;\) C、\(f(x^2+1)=|x+1|\) \(\;\;\; \;\;\;\;\) D、\(f(x^2+2x)=|x+1|\)

分析：利用\(x\)取特殊值，结合函数的定义就能判断。

A、\(f(sin2x)=sinx\) 令\(x=0\)时，\(f(0)=0；x=π/2\)时，则\(sin2x=0\), 即\(f(0)=1\),即出现\(f(0)=0\)和\(1\)，一对多，错误。

B、\(f(sin2x)=x^2+x\) 令\(x=0\)时，\(f(0)=0；x=π\)时，则\(sin2x=0,\) 即\(f(0)=π^2+π,\)即出现\(f(0)=0\)和\(π^2+π\)，一对多，错误。

C、\(f(x^2+1)=|x+1|\) 令\(x=-1\)时，\(f(2)=0；x=1\)时，\(f(2)=2\),即出现\(f(2)=0\)和\(2\)，一对多，错误。

D、\(f(x^2+2x)=|x+1|\) 令\(x+1=t\)，则\(f(x^2+2x)=|x+1|\)化为\(f(t^2-1)=|t|\)，再令\(t^2-1=x\)，则$t=±\sqrt{x+1} $

所以\(f(x)=\sqrt{x+1}\) 所以存在函数\(f(x)=\sqrt{x+1}\),使得\(f(x^2+2x)=|x+1|\)。故选\(D.\)

感悟：相同考法的题目，判断哪个图像不是函数图像，我们的做法就是做x轴的垂线，若垂线和图像有两个及其以上的交点，则一定不是函数图像，因为出现了“一对多”，不符合函数的定义。

$\color{Red}{【004】}$

设分段函数 \(f(x)=\begin{cases} 2x，&x\leq 0 \\\ log_2^{\;\;x} ，&x>0 \end{cases}\)若对任意给定的\(t\in (1，+∞)，\)都存在唯一的\(x\in R，\)满足\(f(f(x))=2a^2t^2+at，\)则正实数\(a\)的最小值是（　　）

A．2 \(\;\;\; \;\;\;\;\) B． \(\cfrac{1}{2}\) \(\;\;\; \;\;\;\;\) C． \(\cfrac{1}{4}\) \(\;\;\; \;\;\;\;\) D． \(\cfrac{1}{8}\)

【分析】此题的突破口在于如何才会存在唯一的\(x\)满足条件，结合\(f(x)\)的值域范围或者图象，易知只有在\(f(x)\)的自变量与因变量存在一一对应的关系时，即只有当\(f(x)>2\)时，才会存在一一对应．

【解答】解：根据\(f(x)\)的函数，我们易得出其值域为\(R，\)

又∵\(f(x)=2x，（x≤0）\)时，值域为\(（0，1]；\) \(f（x）=log_2^x，（x＞0）\)时，其值域为\(R，\)

∴可以看出\(f(x)\)在\(（0，1]\)上有两个解，

要想\(f(f(x))=2a^2t^2+at，\)在\(t\in（1，+∞）\)上只有唯一的\(x\in R\)满足，

必有\(f(f(x))＞1\) （因为\(2a^2t^2+at＞0\)），

所以：\(f(x)＞2，\)解得：\(x＞4\)，

当 \(x＞4\)时，\(x\)与\(f(f(x))\)存在一一对应的关系，

∴\(2a^2t^2+at＞1，t∈（1，+∞），\)且\(a＞0，\)

所以有：\((2at-1)(at+1)＞0，\)解得：\(t＞\cfrac{1}{2a}\)或者\(t＜-\cfrac{1}{a}\)（舍去），

∴\(\cfrac{1}{2a} \leq 1\)，∴\(a\ge \cfrac{1}{2}\)，故选：\(B\)

【点评】本题主要考查了分段函数的应用，本题关键是可以把\(2a^2t^2+at\)当作是一个数，然后在确定数的大小后再把它作为一个关于t的函数．

$\color{Red}{【005】}$

(2014.浙江卷)设\(\theta\)是两个非零向量\(\vec{a},\vec{b}\)的夹角，已知对任意实数\(t\)，\(|\vec{b}+t\vec{a}|\)的最小值是1，（\(\;\;\;\; B\;\;\;\)）

A、若\(\theta\)确定，则\(|\vec{a}|\)唯一确定 \(\;\;\; \;\;\;\;\) B、若\(\theta\)确定，则\(|\vec{b}|\)唯一确定 \(\;\;\;\;\;\;\;\) C、若\(|\vec{a}|\)确定，则\(\theta\)唯一确定 \(\;\;\; \;\;\;\;\) D、若\(|\vec{b}|\)确定，则\(\theta\)唯一确定

分析：利用\(\Delta=0\)，而不是$ \Delta \leq 0 $.
求解：

【法1】\(|\vec{b}+t\vec{a}|≥1\)，则有\(\vec{b}^2+t^2\vec{a}^2+2\vec{a}\vec{b}t≥1\)，即有\(t^2a^2+2|\vec{a}||\vec{b}|\cos\theta\cdot t+b^2-1≥0\)，要保证对任意实数\(t\)，\(|\vec{b}+t\vec{a}|\)的最小值取到1，则必须\(\Delta =0\)，而不是\(\Delta\leq 0\)，故解得\(\Delta=4a^2b^2\cos^2\theta-4a^2(b^2 -1)=0\)，则有\(b^2-1=cos^2\theta\),故选B.

【法2】令\(f(t)=|\vec{b}+t\vec{a}|^2=b^2+t^2a^2+2abt\)，利用二次函数的最小值是1求解，倒是不容易出错。

感悟：同类题，已知开口向上的二次函数的值域是\([0,＋∞)\)，则利用\(\Delta=0\)，而不是\(\Delta \leq 0\).

$\color{Red}{【006】}$

已知映射\(f：A\rightarrow B\)，其中\(A=B=R\)，对应法则\(f：x\rightarrow y= -x^2+2x，\)对于实数\(k\in B\)在集合\(A\)中存在两个不同的原像，则\(k\)的取值范围是（　　）
A．k＞1 \(\;\;\;\;\;\;\;\;\;\;\;\;\) B．k≤1 \(\;\;\;\;\;\;\;\;\;\;\;\;\) C．k＜1 \(\;\;\;\;\;\;\;\;\;\;\;\;\) D．k≥1

分析：∵对于实数\(k\in B\)在集合\(A\)中存在两个不同的原像，∴ $ y=-x^2+2x= -（x^2-2x+1）+1≤1，$ 当\(y=1\)时，有两个相同的\(x\)，不合题意，∴ \(k＜1\)，故选C．

\(\color{Blue}{【对照1】}\)映射\(f：x\rightarrow y=-x^2+2x\)是\(\scriptsize{M}\)到\(\scriptsize{N}\)的映射，\(\scriptsize{M}=\scriptsize{N}=\scriptsize{R}\)，若对任意实数\(\scriptsize{P}\in \scriptsize{N}\)，在\(\scriptsize{M}\)中不存在原象， 则\(\scriptsize{P}\)的取值范围是（　　）

A．[1，+∞） \(\;\;\;\;\;\;\;\;\;\;\;\;\) B．（1，+∞）\(\;\;\;\;\;\;\;\;\;\;\;\;\) C．（-∞，1] \(\;\;\;\;\;\;\;\;\;\;\;\;\) D．（-∞，+∞）

分析:由对应关系\(y=-x^2+2x\)求出以\(R\)为定义域的函数的值域，由补集思想得到集合\(N\)中不存在原像的元素构成的集合，则答案可求．

解析：∵ \(y=-x^2+2x= -(x-1)^2+1≤1\)．

∴ 对于集合\(M=R\)，那么在\(f：x\rightarrow y=-x^2+2x\)的对应下，对应的像的集合为\(\{y|y\leq1\}\)，

∴集合\(N=R\)中，满足\(y＞1\)的元素在\(M\)中不存在原像．即\(P\)的取值范围是\(（1，+∞）\)．

故选：B．【点评】题考查了映射的概念，考查了函数值域的求法，训练了配方法，体现了补集思想，是基础题．

\(\color{Blue}{【对照2】}\)映射\(f：x\rightarrow y=-x^2+2x\)是\(M\)到\(N\)的映射，\(M=N=R\)，若有（存在）一实数\(P\in N\)，在\(M\)中不存在原象， 则\(P\)的取值范围是（　　）
A．[1，+∞）\(\;\;\;\;\;\;\;\;\;\;\;\;\) B．（1，+∞） \(\;\;\;\;\;\;\;\;\;\;\;\;\) C．（-∞，1] \(\;\;\;\;\;\;\;\;\;\;\;\;\) D．（-∞，+∞）

分析：∵\(y=-x^2+2x= -(x-1)^2+1≤1\)． ∴对于集合\(M=R\)，在\(f：x\rightarrow y = -x^2+2x\)的对应下， 对应的像的集合为\(\{y|y≤1\}\)，

∴集合\(N=R\)中，当\(P\in（-∞，1]\) 时，实数\(P\)在\(M\)中必然存在原像。

现要求存在一实数\(P\in N\)，在\(M\)中不存在原象，则\(P\)的取值范围必然要包含\(（-∞，1]\) ， 即\(P\)的取值范围是\(（-∞，+∞）\)．故选：D.

$\color{Red}{【007】}$

已知函数\(f(x)=x^2-ax+a+3\)，\(g(x)=ax-2x\)，若不存在\(x_0\in R\)，使得\(f(x_0)<0\)与\(g(x_0)<0\)同时成立，则实数\(a\)的取值范围是多少？

解析：函数\(f(x)=x^2-ax+a+3\)，对称轴是\(x=\cfrac{a}{2}\)，\(\Delta=a^2-4(a+3)=a^2-4a-12\)，\(g(x)=ax-2x=a(x-2)\)，恒过定点\((2，0)\)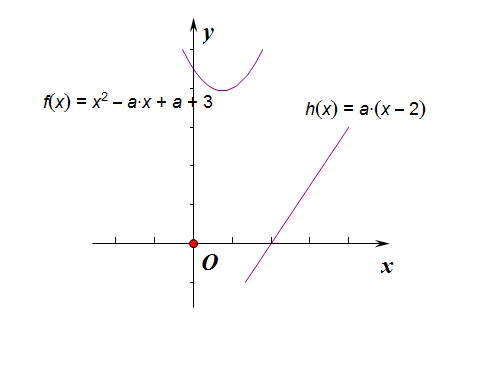

\(1^。\) 当\(a=0\)时，\(f(x)=x^2+3，g(x)=0\)，满足题意。

\(2^。\) 当\(a>0\)时，\(x_0<2\)时，\(g(x_0)<0\)，故只须\(x_0<2\)时，\(f(x_0)\ge0\)恒成立。

只需要\(\begin{cases} &a>0 \\\ &\Delta<0\end{cases}\)或者\(\begin{cases} &a>0 \\\ &\Delta\ge 0 \\\ &\cfrac{a}{2}\ge 2 \\\ &f(2)=7-a\ge 0\end{cases}\)

解得\(0<a<6\)或\(6 \leq a \leq 7\)，故 \(0 <a \leq 7\).

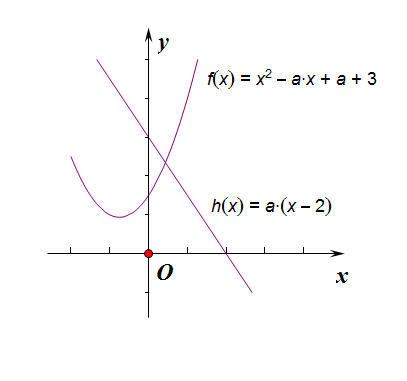
\(3^。\) 当\(a<0\)时，\(x_0>2\)时，\(g(x_0)<0\)，故只须\(x_0>2\)时，\(f(x_0)\ge0\)恒成立。

只需要\(\begin{cases} &a<0 \\\ &\Delta<0\end{cases}\)或者\(\begin{cases} &a<0 \\\ &\Delta\ge 0 \\\ &\cfrac{a}{2}\leq 2 \\\ &f(2)=7-a\ge 0\end{cases}\)

解得\(-2<a<0\)或\(a \leq -2\)，故 \(a < 0\).

综合以上可知，\(a\leq 7\)。

$\color{Red}{【008】}$

【2016-2017宝鸡市第一次质量检测16题】我市在“录像课评比”活动中，。。。

分析：本题考察逻辑与推理中的不完全归纳法，策略：当5节课不好思考时，先减少课时思考；

当只有1节课时，比如结果\((1,优)\)或\((1,差)\)，优秀课最多是1节，

当只有2节课时，比如结果\((2,差)\)或\((1,优)\)，优秀课最多是2节，

当只有3节课时，比如结果\((3,差)\)或\((2,中)\)或\((1,优)\)，优秀课最多是3节，

解释：从第一个维度评判，第一节课是优秀课，从第二个维度评判，第三节课是优秀课，评判第二节课时，由于2>1，中好于差，故第二节课从两个维度都不亚于其他课，那么也是优秀课。

当只有4节课时，比如结果\((4,差)\)或\((3,中)\)或\((2,良)\)或\((1,优)\)，优秀课最多是4节，

当只有5节课时，比如结果\((5,差)\)或\((4,次差)\)或\((3,中)\)或\((2,良)\)或\((1,优)\)，优秀课最多是5节，

转载于:https://www.cnblogs.com/wanghai0666/p/5887378.html