基本概念
下面列出的几个概念有助于理解本文所讨论的主题。
机会过程
书中没有给出机会过程的显式定义,我用搜索引擎也没有找到理想的回答:
但是书中提供了丰富的例子来说明机会过程,括号内是本人为了信息完整性附加的说明:
南非数学家 John Kerrich ... 被拘留在 Jutland 集中营度过战争(二战)的余下岁月,为了消磨时间他进行了一系列概率论的试验,一个试验的内容是抛一枚硬币10000次(并统计获得的头像数)。
轮盘赌输或赢的金额,旋转轮盘是一个机会过程。
在选民的一个随机样本中民主党人的比率,一个机会过程被用于抽取样本。
根据这些例子,机会过程应该是指一系列独立重复的随机试验,并且机会过程可以被抽象为盒子模型。
盒子模型
每次抛硬币可以类比成从一个盒子中有放回地抽卡片,这个盒子里只有两张卡片,上面分别写着 0 和 1。
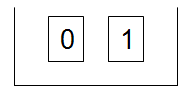
如果用卡片 1 代表头像,则10000次抽取后,所有取得的卡片数字的总和就等于在抛硬币10000次后获得的头像数。
也即,从一个盒子中有放回地抽取标有数字的卡片就是一个机会过程,而我们关注的随机变量是卡片上数字的和。
平均数律
每次从上面的盒子抽取卡片,抽到 0 和 1 的概率分别是 50%。所以10000次抽取后,我们期望获得5000张左右的 1 和5000张左右的 0,二者之和等于10000。这就是平均数律,它告诉人们机会过程的结果是一个随机变量,但它不会偏离平均值太远。
机会变异(机会误差)
机会过程的结果相对于平均值的偏移称为机会误差。
机会误差可以是绝对误差:
10000次抛硬币试验获得的头像总数 - 5000
也可以是相对误差:
absolute(10000次抛硬币试验获得的头像总数 - 5000)/ 5000
机会变异告诉我们:
当抛的次数增加时,头像数与抛的次数的一半之间的差变得较大,但是头像的百分比与50%之间的差异却变得较小。
也即,随着试验次数增加,绝对误差有增大的趋势,而相对误差有减小的趋势。
(机会过程的)期望值
随机放回地从盒子中抽取所得数之和的期望值等于(抽取次数)×(盒平均)
假如有这样一个盒子:
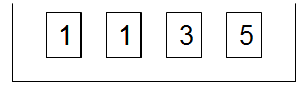
它的盒平均是:
(1+1+3+5)/ 4 = 2.5
如果做100次抽取,我们期望卡片和为:
100 × 2.5 = 250
左右。
机会过程的期望值其实就是之前提到的平均值。
(机会过程的)标准误差SE
平均数律与机会变异定性地描述了机会误差与试验次数之间的关系。而标准误差可以定量地衡量机会误差。
一个和可能在它的期望值附近,但是偏离一个其大小与标准误差相似的机会误差。
在从装有标上数字的卡片的盒中作随机有放回的抽取时,抽得数之和的标准误差是:
SquareRoot ( 抽取次数 ) ×(盒子的SD)
这里的机会误差是绝对误差,SD是盒子中卡片数字的标准差,显示了数字的离散程度。
可以看出机会误差随着抽取次数的增加而增加,但是增加的速度慢于抽取次数;盒子中卡片的数字差异(SD)越大,机会误差就越大。后者不难理解:

这两个盒子具有相同的盒平均(等于5),左边的盒子SD=0,无论抽取多少次都没有机会误差。右边盒子SD>0,它具有机会变异的可能。
程序验证
给出如下盒子模型:
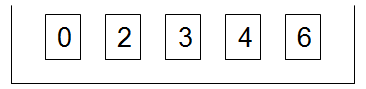
有3种抽取方案,分别是抽取25次、100次和500次,每种方案执行100次。程序和结果如下:
#include <time.h>
#include <math.h>
#include <iostream>
#include <fstream>
#include <string>
using namespace std;
#define random(x) ( rand()%x )
//计算盒平均
double getBoxExpectation(double cards[], int cardNum)
{
double boxExpectation = 0.0;
for (int i = 0; i < cardNum; i++)
{
boxExpectation += cards[i];
}
boxExpectation /= cardNum;
return boxExpectation;
}
//计算卡片标准差
double getBoxSD(double avg, double cards[], int cardNum)
{
double boxSD = 0.0;
for (int i = 0; i < cardNum; i++)
{
boxSD += pow((avg-cards[i]), 2);
}
boxSD /= cardNum;
boxSD = sqrt(boxSD);
return boxSD;
}
void main()
{
int cardNum = 5;
double cards[] = { 0, 2, 3, 4, 6 };
double boxExpectation = getBoxExpectation(cards, cardNum);
double boxSD = getBoxSD(boxExpectation, cards, cardNum);
int trialTimes = 500;
string dataFile = "Box_Experiment_Data_500.txt";
int planTimes = 100;
double planExpectation = boxExpectation * trialTimes;
double planStdErr = sqrt(trialTimes)*boxSD;
double planAvgErr = 0;
ofstream fout(dataFile);
fout << "方案执行数\t和" << endl;
srand((int)time(0));
for ( int plan = 0; plan < planTimes; plan++ )
{
int sum = 0;
for (int trial = 0; trial < trialTimes; trial++)
{
int cardIndex = random(cardNum);
int card = cards[cardIndex];
sum += card;
}
fout << (plan + 1) << "\t" << sum << endl;
planAvgErr += abs(sum - planExpectation);
}
planAvgErr /= planTimes;
fout << "\n期望" << "\t" << planExpectation << endl;
fout << "标准误差" << "\t" << planStdErr << endl;
fout << "平均机会误差" << "\t" << planAvgErr << endl;
fout << "\t" << (planAvgErr / planExpectation)*100 << '%'<<endl;
}

盒平均 = (0+2+3+4+6)/ 5 = 3
所以三个方案的期望分别是:3*25=75, 3*100=300, 3*500=1500
卡片标准差 = 2
所以三个方案的标准误差分别是:squareRoot(25)*2=10, squareRoot(100)*2=20, squareRoot(500)*2=44.72
最后分别求出了3种方案平均机会误差的绝对值和相对值。
从表格中可以看出,随着试验次数的增加,机会误差发生变异,变异的趋势是:
绝对误差增大,相对误差减小。
并且绝对误差在标准误差附近。
补充
【标准差SD】 和 【标准误差SE】 不同。前者衡量一系列数字的离散程度,后者衡量机会过程中的机会变异。
机会过程不是随机过程,因为机会过程的试验之间不具有时间相关性。举例而言,在一个盒子中有放回地抽取100次与同时在100个相同的盒子中抽取一次没有任何区别。
补偿对于平均数律不起作用。举例而言,抛了10次硬币之后获得了10次正面,但平均数律并没有对第11次抛掷获得反面的概率进行补偿,它依然是50%。
当试验次数充分大时,可以利用正态曲线计算机会过程之和落在一定范围内的概率。对于标准正态分布,随机变量落在 [-SD, +SD] 范围内的概率是68%,[-2SD, +2SD] 范围内的概率是95%。类比上面的第二个方案,期望值是300,标准误差是20,对应的1个标准误差范围是 [280, 320],2个标准误差范围是 [260, 340]。经过统计,落在 [280, 320] 内的方案执行数是72个,接近68%的比例;落在 [260, 340] 内的方案执行数是96个,接近95%的比例。






















 3464
3464

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








