分式型函数的相关知识

最新推荐文章于 2024-09-27 11:51:50 发布

weixin_34104341

最新推荐文章于 2024-09-27 11:51:50 发布

阅读量2.3k

点赞数 4

原文链接：http://www.cnblogs.com/wanghai0666/p/9890188.html

版权

一、常见列举

【代数部分】

①分子分母都是一次型，如$f(x)=\cfrac{x+2}{x+1}$；

特别注意：$f(x)=\cfrac{1-x}{1+x}$，对称中心为$(-1，-1)$，且有$\cfrac{1-x}{1+x}\times \cfrac{1+x}{1-x}=1$，故$g(x)=lg\cfrac{1-x}{1+x}$就是奇函数。

原因：$g(-x)=lg\cfrac{1+x}{1-x}=lg(\cfrac{1-x}{1+x})^{-1}=-lg\cfrac{1-x}{1+x}=-g(x)$。

②分子二次型，分母一次型，如$h(x)=\cfrac{x^2-4x+5}{x-2}$，

③分子一次型，分母二次型，如$n(x)=\cfrac{x+1}{x^2+3x+3}$；

④分子分母是一次齐次式，$f(x)=\cfrac{cosx+2sinx}{sinx-2cosx}$；

⑤分子分母是二次齐次式，$h(\theta)=\cfrac{2sin^2\theta+cos^2\theta}{sin^2\theta-3cos^2\theta}$

⑥分母为$1$ 的二次齐次式，$g(\theta)=cos2\theta=\cfrac{cos2\theta}{1}=\cfrac{cos^2\theta-sin^2\theta}{sin^2\theta+cos^2\theta}$

⑦分母之和为定值的类型，$f(x)=\cfrac{1}{x}+\cfrac{4}{2-x}(0<x<2)$

⑧可以转化为上述分式型的，如求函数$y=\cfrac{sin\alpha\cdot cos\alpha}{sin\alpha+cos\alpha}，\alpha\in [0，\cfrac{\pi}{2}]$的值域问题。

⑨线性规划型，如求$\cfrac{3x+4y+10}{x+3}$的取值范围。

⑩线性规划型，如$z=\cfrac{x^2+y^2}{xy}=\cfrac{x}{y}+\cfrac{y}{x}=k+\cfrac{1}{k}$；

⑪函数与导数中的导函数如$f'(x)=\cfrac{(x-2)(x+1)}{x}$；$f'(x)=\cfrac{e^x(x-1)(x+m)}{x^2}$等；

⑪补充变形技巧如下；为了能做出函数$f(x)=\cfrac{x^2}{3-x}$的图像，将函数做以下变形，由于常用，提醒注意理解记忆。

分式中的配凑法变形，$\cfrac{x^2}{3-x}=-\cfrac{x^2}{x-3}=-\cfrac{(x-3)^2+6x-9}{x-3}$

$=-(x-3)-\cfrac{6x-18+9}{x-3}=-(x-3)-\cfrac{9}{x-3}-6$

$=-[(x-3)+\cfrac{9}{x-3}]-6$；

分式中的换元法变形，令$3-x=t$，则$x=3-t$，则$f(x)=\cfrac{x^2}{3-x}=\cfrac{(3-t)^2}{t}$

$=\cfrac{t^2-6t+9}{t}=t+\cfrac{9}{t}-6=(3-x)+\cfrac{9}{3-x}-6$

$=-[(x-3)+\cfrac{9}{x-3}]-6$；

【几何部分】

⑫碰到$d=\cfrac{|k+1|}{\sqrt{k^2+1}}$时，可以考虑先平方得到，$d^2=\cfrac{(k+1)^2}{k^2+1}=1+\cfrac{2k}{k^2+1}\leq 1+1=2$，再考虑求解$d$；

⑬$|OP|^2=\cfrac{(m^2+1)(m^2+16)}{(m^2+4)^2}$，令$m^2+4=\lambda>4$，则$|OP|^2=\cfrac{(\lambda-3)(\lambda+12)}{\lambda^2}=-\cfrac{36}{\lambda^2}+\cfrac{9}{\lambda}+1$

$=-36(\cfrac{1}{\lambda}-\cfrac{1}{8})^2+\cfrac{25}{16}\leq \cfrac{25}{16}$.

⑭

二、常用变形

针对①型的，常用配凑法+分离常数法，或配凑法+分式裂项法，

如$f(x)=\cfrac{x+2}{x+1}=1+\cfrac{1}{x+1}$；

针对②型的，常用配凑法+分离常数法，或配凑法+分式裂项法，或换元法，

如[配凑法]$h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}$，

或[换元法]令$x-2=t$，则$x=t+2$，

故$h(x)=\cfrac{(t+2)^2-4(t+2)+5}{t}=\cfrac{t^2+1}{t}=t+\cfrac{1}{t}$

即$h(x)=t+\cfrac{1}{t}=(x-2)+\cfrac{1}{x-2}$

针对③型的，常用取倒数法，或换元法，或配凑同除法

如$n(x)=\cfrac{x+1}{(x+1)^2+(x+1)+1}=\cfrac{1}{(x+1)+\cfrac{1}{x+1}+1}$

针对④型的，常用分子分母同除以$cosx$法，
针对⑤型的，常用分子分母同除以$cos^2\theta$法，
针对⑥型的，转化为⑤型的再处理；
针对⑦型的，转化为利用均值不等式处理；
针对⑧型的，利用换元转化为上述分式型处理；

如令$sin\alpha+cos\alpha=t=\sqrt{2}sin(\alpha+\cfrac{\pi}{4})\in [1，\sqrt{2}]$，

则$sin\alpha\cdot cos\alpha=\cfrac{t^2-1}{2}$，

则原函数转化为$y=\cfrac{\frac{1}{2}(t^2-1)}{t}=\cfrac{1}{2}(t-\cfrac{1}{t})，t\in [1，\sqrt{2}]$

针对⑨型的，化为部分分式的形式，转化为斜率型，由数转化为形。

如求$\cfrac{3x+4y+10}{x+2}=\cfrac{(3x+6)+4y+4}{x+2}=3+4\times \cfrac{y+1}{x+2}=3+4\times \cfrac{y-(-1)}{x-(-2)}$的取值范围。

三、隐含性质

①如$f(x)=\cfrac{x+2}{x+1}=1+\cfrac{1}{x+1}$，则可知其对称中心为$(-1，1)$，

则其必然满足关系：$f(x)+f(-x-2)=2$或者$f(-x)+f(x-2)=2$。

如若不信，你可以验证，$f(-x)=\cfrac{-x+2}{-x+1}=\cfrac{x-2}{x-1}$；

$f(x-2)=\cfrac{x-2+2}{x-2+1}=\cfrac{x}{x-1}$，则$f(-x)+f(x-2)=\cfrac{x-2+x}{x-1}=\cfrac{2(x-1)}{x-1}=2$；

其实，表达式$f(-x)+f(x-2)=2$就是刻画函数的对称性的。

②同理同法，我们可知函数$h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}$，

是中心对称的，其对称中心为$(2，0)$。也就是说，其必然满足$f(x)+f(4-x)=0$。

四、典例剖析

例1

求函数$f(x)=\cfrac{2+x}{1+x}$的值域。

分析：函数$f(x)=\cfrac{2+x}{1+x}=1+\cfrac{1}{1+x}$，由于$\cfrac{1}{1+x}\neq 0$，则函数$f(x)\neq 1$，故值域为$(-\infty，1)\cup (1，+\infty)$。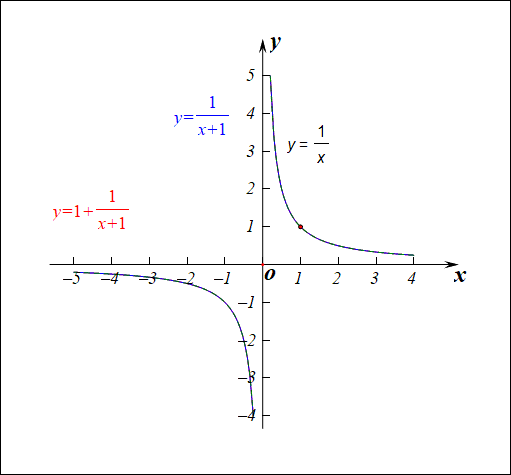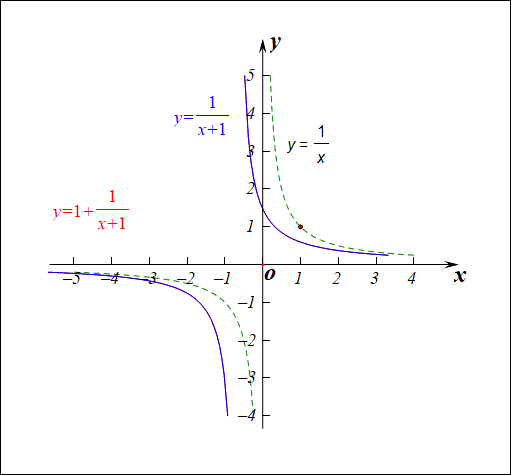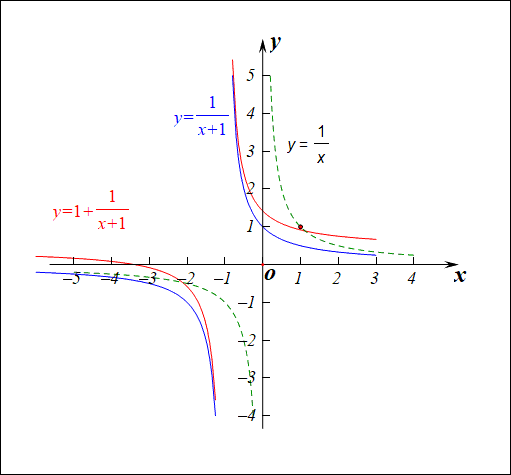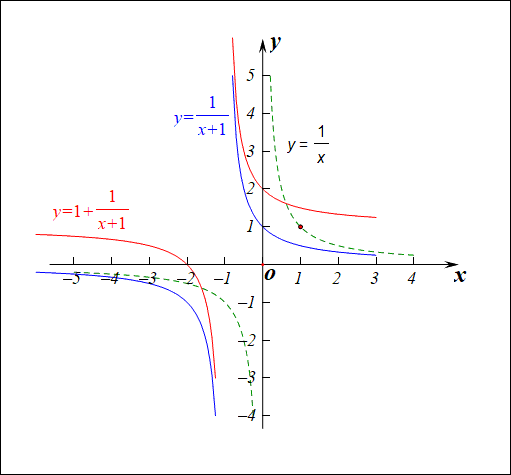

1、此类函数是高三的高频函数，其图像常用变换作图得到，

作图顺序：$y=\cfrac{1}{x}\xrightarrow{向左1个单位}y=\cfrac{1}{x+1}\xrightarrow{向上1个单位} y=1+\cfrac{1}{x+1}$，

这样的作图变换我们一般要求学生要非常熟练的掌握。

2、函数$f(x)=\cfrac{2+x}{1+x}$是中心对称图形，由变换作图的过程就可以知道对称中心是$(-1，1)$，其对称性的表达形式满足关系：$f(x)+f(-2-x)=2$，

这时对称中心图形的另外一种等价且较抽象的说法。注意：满足关系$f(x)+f(-2-x)=2$，等价于这个函数有对称中心$(-1，1)$，

但是这样的函数不一定就非得是这个函数，因为满足这个关系的函数不止一个。

3、向$y$轴作正射影，就能很容易的得到值域。这个方法也可以叫做图像法。
4、函数变换后得到$f(x)=1+\cfrac{1}{1+x}$，其中第一个$1$，就是从分式中分离出来的常数，为什么这样做？

主要是基于变量集中。变形前的分式的分子分母中都有变量$x$，变形后，只有后面的部分含有变量，前面仅仅是常数，

得到这样的表达式后我们要继续研究函数的其他性质往往就更容易些，这样的变形方法也叫部分分式法。

延伸阅读

5、还有那些相关知识？

1、本方法做以抽象归纳，则一般这样的函数都能用此方法：函数为分式函数，且分子分母都是一次式，

比如$f(x)=\cfrac{ax+b}{cx+d}$型，其中$a，b，c，d\in R$.

2、相关延伸：函数为分式函数，且分子分母中一个是一次式，一个是二次式，这样的变形对照本方法叫“分离变量法，

”比如$h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\xrightarrow{x-2=t}t+\cfrac{1}{t}$，

常常会朝向对勾函数转化，也是一个高频变形。

一、为什么要研究常用模板函数

比如我们常常把函数$f(x)=x+\cfrac{1}{x}$作为模板，意思是对这个函数的大致图像我们要掌握的非常熟练。那么我们为什么要把函数$f(x)=x+\cfrac{1}{x}$作为模板来看呢？

请大家先看一个函数$h(x)=\cfrac{x^2-4x+5}{x-2}$，这个函数在高三数学学习中应该很常见，初次接触我们感觉很恐怖，心里都没有底，主要原因是不知道这个函数的图像和性质到底是什么样的。

别着急，慢慢看，我们对这个函数做个变换，

$h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\xrightarrow{x-2=t}t+\cfrac{1}{t}$，

看到变换最后的函数$g(t)=t+\cfrac{1}{t}$，应该不陌生，看着眼熟吧，这时候你还害怕吗？对了，我们心里稍稍安稳了一些，通过模板函数的图像变换就可以搞定它，那你还害怕什么呢？

具体变换思路：先做出函数$f(x)=x+\cfrac{1}{x}$，然后将函数$f(x)$的图像向右平移2个单位，得到函数$f(x-2)$，

也就是函数$f(x-2)=(x-2)+\cfrac{1}{x-2}=\cfrac{(x-2)^2+1}{x-2}=\cfrac{x^2-4x+5}{x-2}=h(x)$，不是很简单吗？如右图所示，当我们把模板函数的性质研究的透透的，对于函数$h(x)$的图像和性质不也就知道了吗？

比如给出的这些貌似恐怖的函数，通过变换我们都能找到它们的模板函数

$f(x)=\cfrac{x^2+2x+2}{x+1}$；$g(x)=\cfrac{x^2+2x}{x+1}$；$m(x)=\cfrac{x^2+3x+3}{x+1}$；

$n(x)=\cfrac{x+1}{x^2+3x+3}$；$l(t)=\cfrac{1+t^2}{1+2\sqrt{2}t}$；$h(x)=\cfrac{x^2-4x+5}{x-2}$；

例2

若$f(x)=\cfrac{3x-2}{2x-1}$，则$f(\cfrac{1}{11})+f(\cfrac{2}{11})+f(\cfrac{3}{11})+\cdots+f(\cfrac{10}{11})$的值是多少？

法1：结合要求解的条件，我们尝试求解$f(x)+f(1-x)$的值，结果会发现：$f(x)+f(1-x)=3$，

故有$f(\cfrac{1}{11})+f(\cfrac{10}{11})=3$;$f(\cfrac{2}{11})+f(\cfrac{9}{11})=3$；等等，

所以$f(\cfrac{1}{11})+f(\cfrac{2}{11})+f(\cfrac{3}{11})+\cdots+f(\cfrac{10}{11})$

$=5[f(\cfrac{1}{11})+f(\cfrac{10}{11})]=5\times 3=15$.

法2：将函数$f(x)$化为部分分式为$f(x)=\cfrac{3}{2}-\cfrac{1}{2(2x-1)}$，

故函数$f(x)$的对称中心是$(\cfrac{1}{2}，\cfrac{3}{2})$，

故根据函数的对称性的数学表达可以写出$f(x)+f(1-x)=3$；

故所求式等于$5\times 3=15$.

法3：本题目也可以说明倒序相加求和法。

例3【限定条件以隐含条件的形式给出】

求$f(x)=\cfrac{1}{x}+\cfrac{4}{2-x}(0< x <2)$的最小值。

详解：注意到隐含条件$x+(2-x)=2，x>0，2-x>0$，则容易看到题目其实为

已知$x+(2-x)=2$，$x>0，2-x>0$，求$f(x)=\cfrac{1}{x}+\cfrac{4}{2-x}(0< x <2)$的最小值。

$f(x)=\cfrac{1}{x}+\cfrac{4}{2-x}$

$=\cfrac{1}{2}(\cfrac{1}{x}+\cfrac{4}{2-x})\times 2$

$=\cfrac{1}{2}(\cfrac{1}{x}+\cfrac{4}{2-x})[x+(2-x)]$

$=\cfrac{1}{2}(1+4+\cfrac{2-x}{x}+\cfrac{4x}{2-x})$，

$\ge \cfrac{1}{2}(5+2\sqrt{4})=\cfrac{9}{2}$，

当且仅当$\cfrac{2-x}{x}=\cfrac{4x}{2-x}$且$0<x<2$时，

即$x=\cfrac{2}{3}$时取得等号。

故$f(x)$的最小值为$\cfrac{9}{2}$。

【引申】求$f(x)=\cfrac{x+1}{x}+\cfrac{6-x}{2-x}(0< x <2)$的最小值。

分析：$f(x)=1+\cfrac{1}{x}+\cfrac{4}{2-x}+1$

$=2+\cfrac{1}{x}+\cfrac{4}{2-x}$

例4【已知单调性求参数的取值范围】

若函数$f(x)=(x^2-cx+5)\cdot e^x$在区间$[\cfrac{1}{2}，4]$上单调递增，则实数$c$的取值范围是【】

$A(-\infty，2]$ $B(-\infty，4]$ $C(-\infty，8]$ $D[-2，4]$

分析：由题目可知，$f'(x)\ge 0$在区间$[\cfrac{1}{2}，4]$上恒成立，

$f'(x)=(2x-c)e^x+(x^2-cx+5)e^x=(x^2-cx+2x-c+5)e^x\ge 0$，

即$x^2-cx+2x-c+5\ge 0$，分离参数得到，

即$cx+c\leq x^2+2x+5$在区间$[\cfrac{1}{2}，4]$上恒成立，

即$c\leq \cfrac{x^2+2x+5}{x+1}$在区间$[\cfrac{1}{2}，4]$上恒成立，

令$h(x)= \cfrac{x^2+2x+5}{x+1}= \cfrac{x^2+2x+1+4}{x+1}=x+1+\cfrac{4}{x+1}\ge 2\sqrt{4}=4$，

当且仅当$x+1=\cfrac{4}{x+1}$，即$x=1\in [\cfrac{1}{2}，4]$时取到等号；

故$c\leq 4$，故选$B$。

例5【2017宝鸡中学高三理科第一次月考第10题】
已知函数$f(x)=\cfrac{2sinxcosx}{1+sinx+cosx}$，$x\in(0，\cfrac{\pi}{2}]$的最大值为$M$，最小值为$N$，则$M-N=$？

分析：令$sinx+cosx=t$ ，由于$x\in(0，\cfrac{\pi}{2}]$，则$t=sinx+cosx=\sqrt{2}sin(x+\cfrac{\pi}{4})\in [1，\sqrt{2}]$，

则$2sinxcosx=t^2-1$，故$f(x)=\cfrac{t^2-1}{t+1}=g(t)=t-1$，

故$f(x)_{max}=M=\sqrt{2}-1$；$f(x)_{min}=N=0$；即$M-N=\sqrt{2}-1$。

例6【2018广东中山期末】已知$\cfrac{1}{3}\leq k<1$，函数$f(x)=|2^x-1|-k$的零点分别为$x_1$、$x_2$，$(x_1<x_2)$，函数$g(x)=|2^x-1|-\cfrac{k}{2k+1}$的零点分别为$x_3$、$x_4$，$(x_3<x_4)$，则$x_4+x_2-(x_3+x_1)$的最小值为【】

$A.1$ $B.log_23$ $C.log_26$ $D.4$

【法1】：函数$f(x)$的零点问题，转化为函数$y=|2^x-1|$与$y=k$的图像交点的横坐标问题，同理，函数$g(x)$的零点问题，转化为函数$y=|2^x-1|$与$y=\cfrac{k}{2k+1}$的图像交点的横坐标问题，

又由于$y=\cfrac{k}{2k+1}=\cfrac{1}{2+\frac{1}{k}}$，在$k\in [\cfrac{1}{3}，1)$上单调递增，即当$k$的取值从$\cfrac{1}{3}$增大到$1$时，$\cfrac{k}{2k+1}$的取值对应的从$\cfrac{1}{5}$增大到$\cfrac{1}{3}$，

做出如下的图像，从图像入手分析，当$y=k$向上平移时，$x_2-x_1$逐渐增大，同理对应的$x_4-x_3$逐渐增大，所以要使得$x_4+x_2-(x_3+x_1)$取到最小值，则需要$x_4-x_3$和$x_2-x_1$同时取到最小值，此时$k=\cfrac{1}{3}$，同时对应的有$\cfrac{k}{2k+1}=\cfrac{1}{5}$；

此时，$|2^{x_2}-1|=\cfrac{1}{3}$，即$2^{x_2}-1=\cfrac{1}{3}$，解得$x_2=log_2\cfrac{4}{3}$，又$|2^{x_1}-1|=\cfrac{1}{3}$，即$1-2^{x_1}=\cfrac{1}{3}$，解得$x_1=log_2\cfrac{2}{3}$，

同理对应的有$|2^{x_4}-1|=\cfrac{1}{5}$，即$2^{x_4}-1=\cfrac{1}{5}$，解得$x_4=log_2\cfrac{6}{5}$，又$|2^{x_3}-1|=\cfrac{1}{5}$，即$1-2^{x_3}=\cfrac{1}{5}$，解得$x_3=log_2\cfrac{4}{5}$，

故此时$[x_4+x_2-(x_3+x_1)]_{min}=(log_2\cfrac{6}{5}-log_2\cfrac{4}{5})+(log_2\cfrac{4}{3}-log_2\cfrac{2}{3})=log_23$，故选$B$。

【法2】：由题可知，$2^{x_2}-1=k$，$1-2^{x_1}=k$，故有$2^{x_2}=k+1$，$2^{x_1}=1-k$，则$2^{x_2-x_1}=\cfrac{1+k}{1-k}$；

同理，$2^{x_4}=1+\cfrac{k}{2k+1}=\cfrac{3k+1}{2k+1}$，$2^{x_3}=1-\cfrac{k}{2k+1}=\cfrac{k+1}{2k+1}$，则$2^{x_4-x_3}=\cfrac{3k+1}{k+1}$；

则$2^{x_4-x_3}\cdot 2^{x_2-x_1}=\cfrac{3k+1}{k+1}\cdot \cfrac{1+k}{1-k}=\cfrac{3k+1}{1-k}$，

又$\cfrac{3k+1}{1-k}=\cfrac{-(-3k+3)+4}{1-k}=-3+\cfrac{4}{1-k}$，

由于$\cfrac{1}{3}\leq k<1$，则$0<1-k\leq \cfrac{2}{3}$，则$\cfrac{4}{1-k}\ge 6$，则$-3+\cfrac{4}{1-k}\ge 3$，

即$2^{(x_4-x_3)+(x_2-x_1)}\ge 3$，则$(x_4-x_3)+(x_2-x_1)\ge log_23$，故选$B$。

例7已知函数$f(x)$是$R$上的偶函数，且对任意互异的实数$x_1，x_2\in [0，+\infty)$，都有$(x_1-x_2)\cdot $ $[f(x_1)-f(x_2)]>0$成立，若实数$x、y$满足不等式$f(x-2)\ge f(y-4)$，则当$x\in [1，2]$时，$\cfrac{xy}{3x^2+xy-2y^2}$的取值范围是_________.

分析：本题目是线性规划形式给出双变量$x、y$的取值范围，求双变量函数的取值范围问题，比较复杂。

先由函数是偶函数可知，$f(|x-2|)\ge f(|y-4|)$，再由其单调性知道$|x-2|\ge |y-4|$，

去掉绝对值符号得到$- |x-2|\leq y-4 \leq |x-2| $ ，

又因为$x\in[1，2]$，则$x-2\in[-1，0]$，故$x-2\leq y-4\leq2-x$，

即$\begin{cases}&x-2\leq y-4 \\ & y-4 \leq 2-x \\ & 1 \leq x \leq 2 \end{cases}$，做出如图的可行域；

接下来用变量集中策略减少变量的个数，具体变换如下：

又$\cfrac{xy}{3x^2+xy-2y^2}=\cfrac{\cfrac{xy}{x^2}}{\cfrac{3x^2+xy-2y^2}{x^2}}$

$=\cfrac{\cfrac{y}{x}}{3+\cfrac{y}{x}-2(\cfrac{y}{x})^2}=\cfrac{t}{3+t-2t^2}$

$=\cfrac{1}{\cfrac{3}{t}+1-2t}(\cfrac{y}{x}=t)$，

此时需要借助可行域判断$t$的范围，结合可行域图像以及$t$的几何意义(经过可行域内的动点和原点的直线的斜率)，

可知$t\in [2，5]$，故至此问题转化为已知$t\in [2，5]$，求$g(t)=\cfrac{1}{\cfrac{3}{t}+1-2t}$的取值范围问题；

令$h(t)=-2t+\cfrac{3}{t}+1$，$h'(t)=-2-\cfrac{3}{t^2}<0$，故$h(t)$在$t\in [2，5]$单调递减，