扩散谱成像的研究进展

2019独角兽企业重金招聘Python工程师标准>>>

磁共振扩散成像（diffusion Magnetic Resonance Imaging, dMRI）是目前惟一一种能够无侵入性地检测白质微观组织结构完整性的技术。其中，基于高斯模型的扩散张量成像（Diffusion Tensor Imaging, DTI）是最流行的dMRI技术，它已经被广泛应用到各种临床疾病的研究中[1-3]。然而，最近的研究发现大脑中很多组织的体素内存在多方向纤维束[4]。由于dMRI的空间分辨率一般是毫米级而水分子的扩散是微米（1毫米=1000微米）级的，单个体素内存在着成千上万种的扩散种类，水分子的平均扩散不一定符合高斯分布。因此，DTI受单高斯模型的限制无法揭示体素内多方向纤维束。扩散谱成像是一种不依赖于模型的多b值多方向的q空间成像[5]，该方法利用概率密度函数描述扩散运动完整的空间分布，以优异的角分辨率精确辨别出局部复杂交错的纤维走行。随着扩散谱成像（Diffusion Spectrum Imaging, DSI）的发展，大量的研究工作围绕着改善数据采集方式、减少扫描时间、提高角分辨率和普及临床应用等问题展开，使得这种方法成为扩散成像领域的一个研究热点。

1 扩散谱成像的基本原理

1.1 原理

在Stejskal-Tanner实验中，扩散信号随相位离散成e指数衰减：

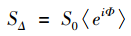(1)

S0表示未加扩散梯度时的MRI信号，Φ表示扩散梯度引起的相位离散，SΔ表示施加扩散梯度后的MRI信号。假设两个扩散敏感梯度的间隔时间Δ远大于梯度持续时间δ，这时候水分子的离散相位：

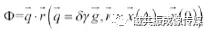。公式中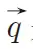，是回波矢量，γ是氢质子的磁旋比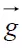，是扩散梯度。r是水分子在扩散时间Δ内的相对位移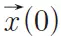，和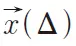分别是水分子在第一个扩散梯度磁场和第二个扩散梯度磁场开始时的位置。如果把水分子的平均扩散看成是期望值，那么可以得到扩散信号和弥散概率密度函数如下关系：

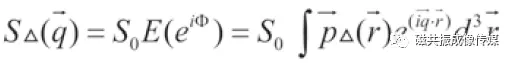(2)

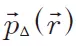（Probability Density Function, PDF）表示一个体素内平均相对自旋位移的密度。

为了排除宏观运动（比如头动）的影响[6]， DSI使用信号模进行傅里叶逆变换得到概率密度函数：

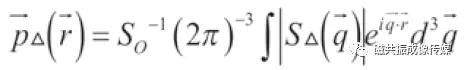(3)

这里的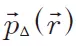是通过傅里叶变换得来的，所以我们称它为扩散谱。

尽管DSI的理论要求扩散梯度磁场间隔时间远大于扩散梯度磁场持续时间，但在实际应用中受硬件条件的限制，这个假设一般不能满足。Wedeen等[6]进一步证实，即使扩散梯度磁场持续时间无法忽略，等式(3)依然成立。

1.2 数据采集和处理

DSI使用笛卡尔网格策略在一个球体内采集q空间的数据点。通常情况下扫描序列的梯度方向数至少需要200以上，最大b值要求8000 s/mm2以上，导致扫描时间长达数十分钟甚至1 h以上，这严重阻碍了其应用到临床上。DSI数据的常规处理步骤如下：（1）数据去噪（比如，加汉宁窗函数，卡阈值，小波去噪等）；（2）对弥散信号的模进行3D反傅里叶变换得到PDF；（3）对PDF进行径向积分得到水分子扩散方向分布函数（Orientation Density Function, ODF），使用ODF描绘纤维束的方向分布；（4）利用ODF计算一些定量指标（比如Generaliz