矢量分解定理的证明

 

注意，在本文中，所有矢量都被描述成一个k维坐标，表示一条从原点到此点的矢量（我懒啊）（没有起点又怎样，表示方法简单啊）

 

先抄一下书描述一下这个定理：如果空间上的三个矢量不共面，那么对于任意矢量p，一定存在一个且仅一个有序实数组x、y、z，使得 p = xa + yb + zc。

 

太难了。不会啊。不行了。tql。awsl。

 

于是先来看更一般的情况（hahaha我也不知道为啥）。

一维坐标系上的任意矢量a都可以用其他任意非零矢量p用kp的方式表示（k是实数）。

这很简单，将a乘上（1/p的长度）,再乘上目标向量的长度和方向即可。

 

然后这能说明什么呢？我也不知道。

 

看比较不一般的情况。

二维的描述是：任意一个二维矢量都可以用两个二维矢量分别乘某两个实数来表示（矢量是不共线的哦，后文会解释）。

 

首先先来看线段的定义：两个相异点的凸组合的集合。

两个相异点P₁、P₂的凸组合是指满足下列点P₃的集合：对某个0 <=σ<= 1,有P₃=σP₁+(1-σ)P_2。

这个式子怎么来的？它意味着什么？

看图~

 

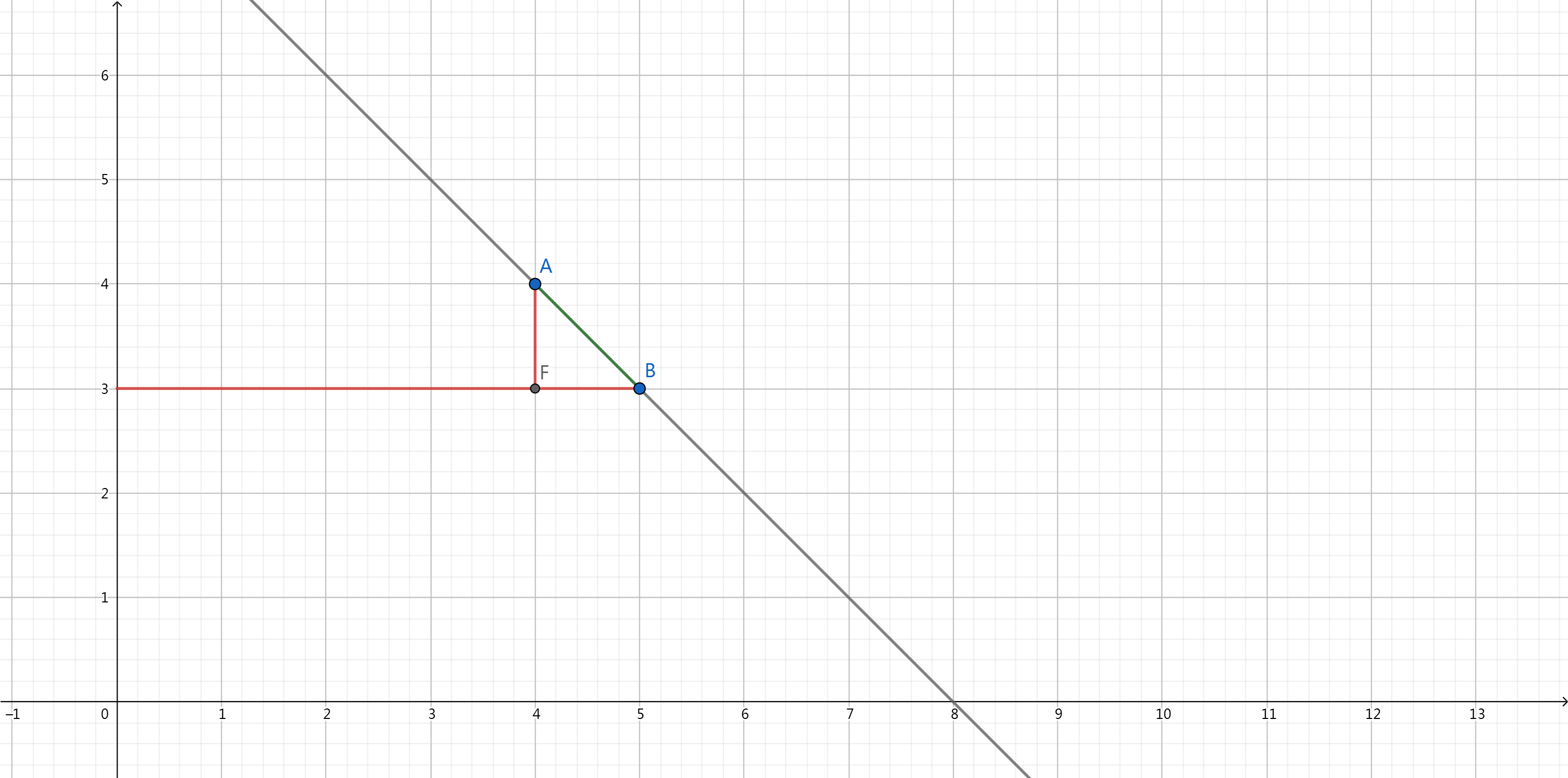
 可以看到A、B点确定了一条直线，在这条直线上，每个x坐标都有唯一的一个y坐标对应，就是y = f（x）嘛~

 这表明，如果要确定线段AB上的一点，只需要确定它的x坐标就可以了。

而线段AB上的任一点的x坐标都可以用（点A的x坐标）+ k(点B的x坐标 - 点A的x坐标)来表示。（k是一个实数）

于是某个式子就是这么来的。然后某个表示方法说明的东西也明朗了（可能吧~）。

然后这个式子意味着什么呢？

都说了表示一个矢量可以用坐标表示，那么……以矢量A的终点和矢量B的终点表示的线段上的点为终点的矢量我们就可以表示出来了!

但这还远远不够啊？

于是由于矢量是可以缩放的……

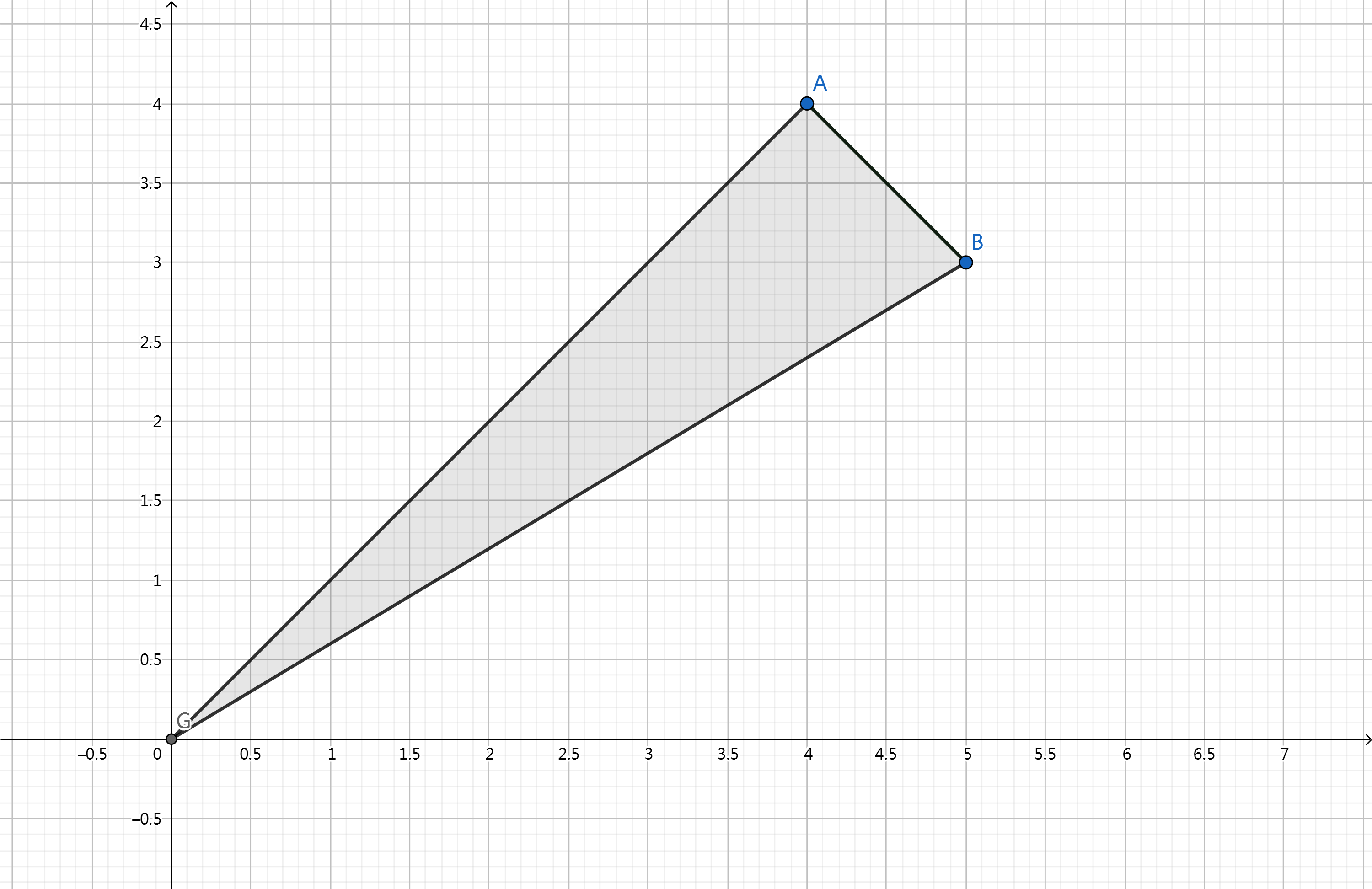
某些矢量也可以用这个方法表示了！同样地，将A、B同时缩放到无穷大，那么某一区块的矢量就都可以由A、B两个矢量以kA + mB的形式表示出来！

可是，这还不够啊？

剩下的就由图片来解释吧，我太懒了……当然下图也可以解释为什么A、B不能共线。

 

---

 

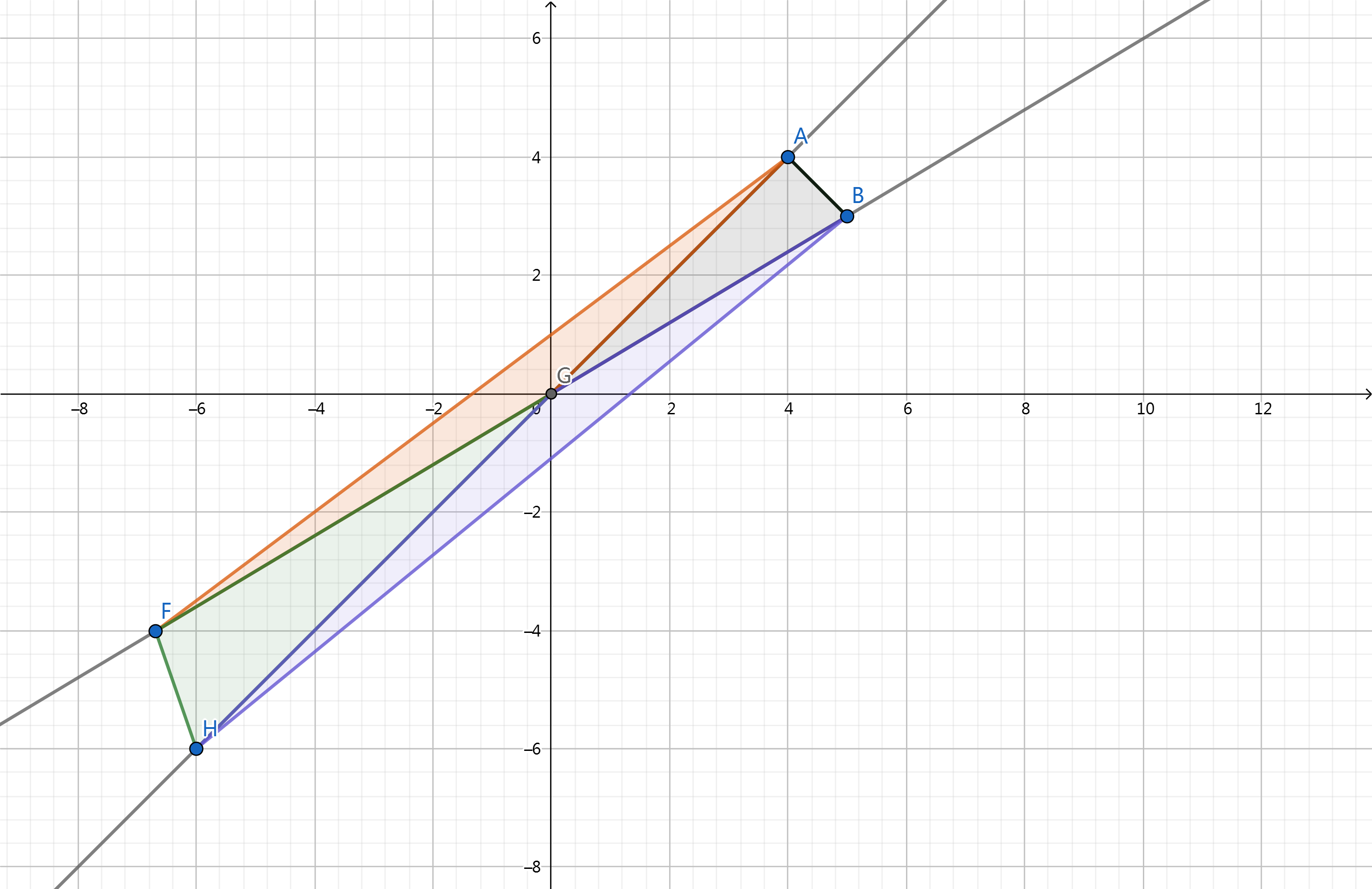
进入正题

先回去读一遍题？我还是有良心的：（先抄一下书描述一下这个定理：如果空间上的三个矢量不共面，那么对于任意矢量p，一定存在一个且仅一个有序实数组x、y、z，使得 p = xa + yb + zc。）

首先如果三个三维矢量不共面，那么它们的终点可以表示一个平面~

要证明的啊~

类比二维的线段，三维的平面也可以用三个三维点来表示啊。

那么对于这个平面，同样有一个函数（其实我不知道有没有啦）f（x，y），对应着唯一的一个z。

于是就可以专心地避开z坐标不谈啦，我们所需要证明的就是二维坐标轴上的一个三角形内部及其边上的所有点都可以用它的顶点来表示。

又是上图的时间了~

 

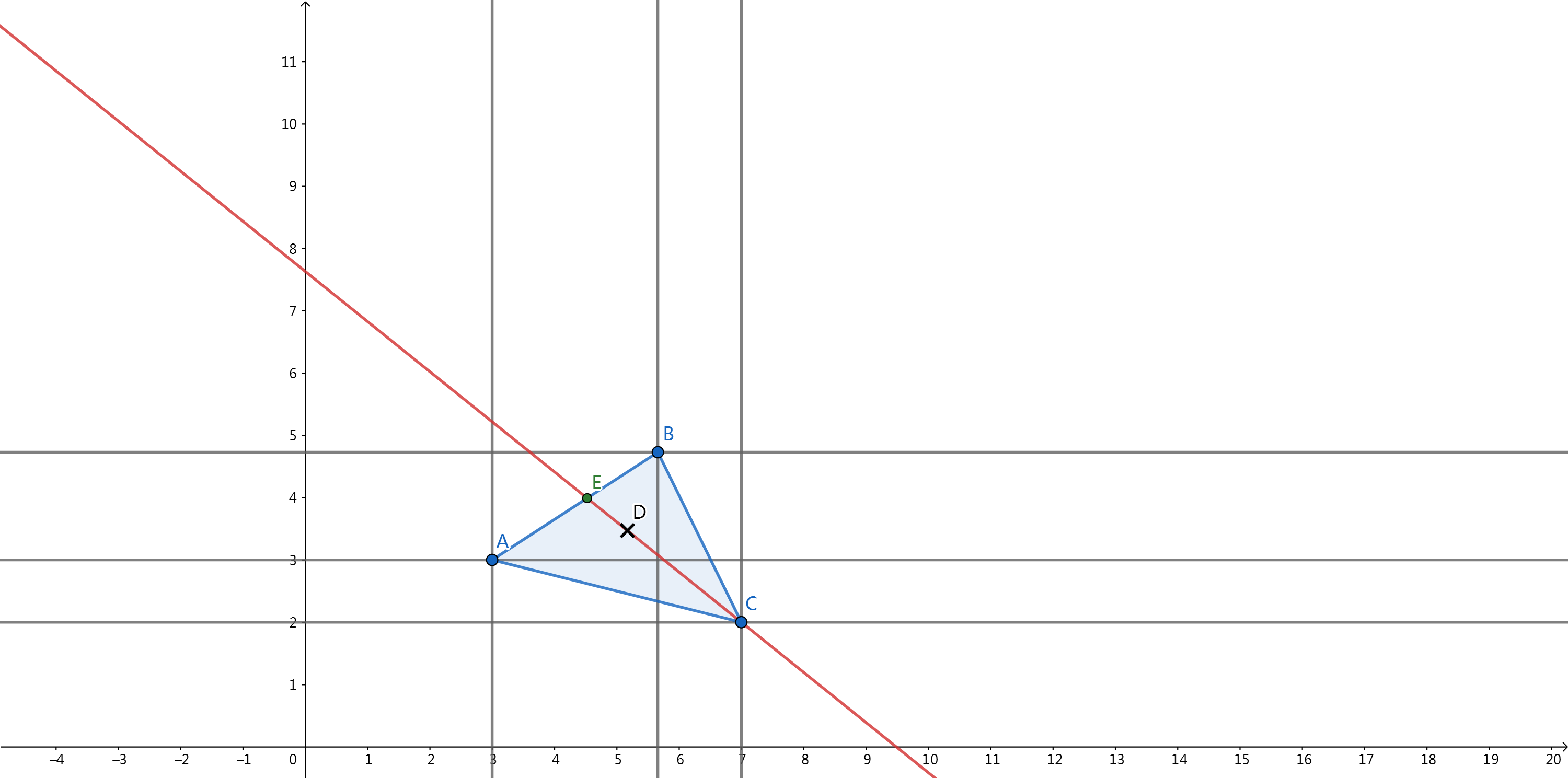
可以看出，对于三角形内随意一点D都可以当做点C和AB上一点E连成的线段上的点·~

所以可以这样表示此三角形内的一点D：PKA + PMB + QC （即PE + QC，其中E：（KA + MB））.

剩下的交给读者自己吧，我太懒了。

---

 

 

本篇纯属娱乐啊，不严谨的地方请指出啦。

转载于:https://www.cnblogs.com/tztqwq/p/10858423.html