本文回顾三维空间中矢量的一些基本概念,虽然这些知识在高中数学中就已学到,但真的是会经常忘记
1.坐标系相关内容
1.1 单位矢量(Unit vector)
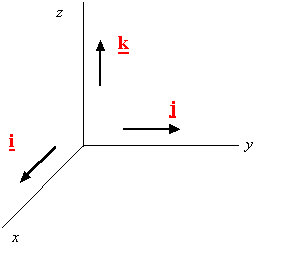
如下图所示,矢量
i−
、
j−
、
k−
分别是长度为1的矢量(即单位矢量)
1.2 坐标基(Base vectors for a rectangular coordinate system)
三个相互正交的单位矢量
1.3 右手系(Right handed system)
由满足右手螺旋准则的三个相互正交的单位矢量构成的坐标系,上图就是一个由坐标基 i− 、 j− 、 k− 构成的右手坐标系
2.矢量
2.1 矢量的坐标分量(Rectangular component of a Vector)
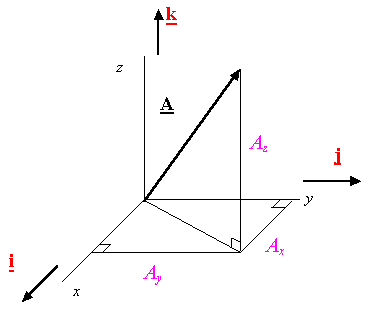
矢量
A−−
沿着坐标系的三个轴上的投影
Ax
、
Ay
、
Az
即为矢量
A−−
的坐标分量,如下图所示:
2.2 矢量的表示
空间矢量可以利用它的三个坐标分量和坐标基表示,上图的矢量
A−−
可以表示如下:
矢量 A−− 的坐标为: (Ax,Ay,Az)
2.3 矢量的方向角和方向余弦
- 方向角:矢量与坐标轴的夹角
- 方向余弦:方向角的余弦
任何一个矢量的方向都可以由它的方向角来决定
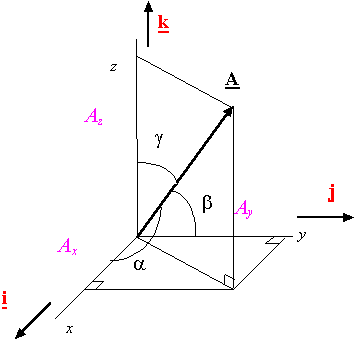
如下图所示, α,β,γ 分别是矢量 A−− 的三个方向角、 cos(α),cos(β),cos(γ) 分别是矢量 A−− 的三个方向余弦
2.4 矢量的矢量分量和它的方向余弦之间的关系
矢量
A−−
的长度为
A
:
那么,矢量的矢量分量和它的方向余弦之间的关系可以表示如下:
反之:
注:
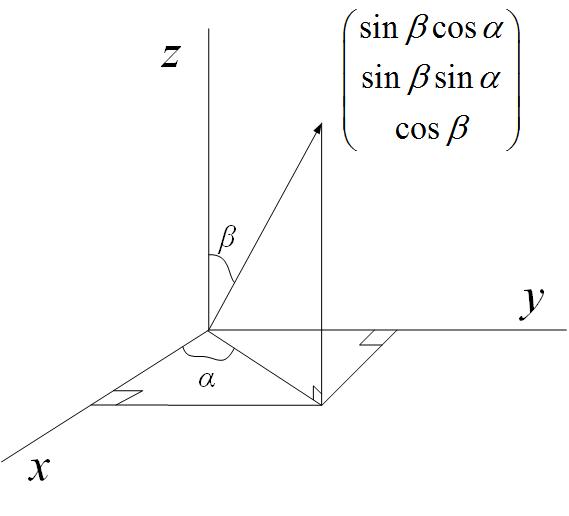
矢量方向向量的另外一种表示:








 本文详细介绍了三维空间中矢量的基本概念,包括单位矢量、坐标基、右手系,以及矢量的坐标分量、方向角和方向余弦的关系。通过坐标轴的投影和方向角的定义,阐述了矢量的表示和特性。
本文详细介绍了三维空间中矢量的基本概念,包括单位矢量、坐标基、右手系,以及矢量的坐标分量、方向角和方向余弦的关系。通过坐标轴的投影和方向角的定义,阐述了矢量的表示和特性。
















 927
927

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








